自転車

こんにちは，なんとなくです．遠心力をご存知なら，慣性の法則は知っていますよね．質量の大きな物体はなかなか動かしにくく（止まっているものは止まっていようとする），動き始めれば今度はなかなか止まらない．これは速度×質量で表される，運動量は大きなほど変化しにくい（変化させるには大きな力がいる）ことを示している，「経験則」です．これと同様に，回転する物体は「回転慣性」と呼ぶものがあります．これも質量の大きなものほど，速く回転するものほど，その回転をとめるのに大きな力がいります．慣性の法則の回転版だと思えばいいですね．通常の慣性は速度が向いている方向に生じていると思えばいいですが，回転体ではどうでしょう．回っている部分は一定の方向を向いていませんが，回転軸だけは別です．回転の止めにくさは，この軸の向きを変えにくいという性質と見ることもできます．コマも自転車も回転軸が一旦決まれば，少しの力ではその向きを変えることはできない，言い換えれば倒れにくいように見えます．これをジャイロ効果と言いますが，その本質は慣性です．遠心力とは関係ないと思います．ではなぜ慣性があるのか，これは質量の起源と関わり，今は先ほど書いたように「経験則」だと思うのが妥当でしょう．こんなんで，どうでしょう．

Re: 自転車

zoro さんのレス (2007/05/26(Sat) 18:17)

＞同じく遠心力は左右で釣り合ってて，力を合成すると，止まっているときと変わらないのでは？

仰るとおりに，遠心力は車輪全体を外側に広げる効果を持ちます．もし車輪が伸びるようであれば問題になりますが，強度が確保されているかぎり，なにも影響しません．

この前，自動車で音速を超えるVTRを見ましたが，ゴムの車輪では，遠心力で破断してしまうので金属のホイールそのものを使うような話だったと思います．

＞なんでコマは回っていると倒れないのでしょうか？

大小のコマを買うか作るかして，回転させて見ると大きなコマのほうが長く倒れないことが判るとおもいます．

定量的に説明するのは難しいですが，大きいコマのほうが回転のエネルギが大きく倒れ難いです．

でも，どうしても知りたければ大学のレベルの力学の本を読んで，さらに知りたければ，ここに書き込んで下さい．詳しい解説書を探してみます．そのぐらい面倒な話になるとおもいます．

Re: 自転車

toorisugari no Hiro さんのレス (2007/05/26(Sat) 20:55)

いろいろな説明法があり，本当はこういう文字での伝達には，数学の力を借りるのが一番なのですが，数学を使わずに，できるだけ説明してみましょう．絵を書けませんので冗長でわかりにくい説明になりますが，ご自分で絵を描きながら読んでください．

自転車の前輪を浮かした状態で回転させます．ハンドルを持った人が右に車体を倒そうとすると，前輪はハンドル軸を中心に時計回りの回転をします．(これを利用して手放し運転が出来ますね．)

回転しているコマにおいて，加える力の向きと動く方向は一致しません(回転が速ければ直角に近い)．

これを考えていきましょう．

今，z軸が紙面の縦方向，x軸が横向きで左から右に行く方向，y軸が紙面垂直手前方向を向くように採りましょう．

z軸に回転軸を持ち，z軸と右ねじの関係ができるように回転しているコマを考えます．(原点に下端が固定されていると考えます．ただし，コマの回転，回転軸の方向変化に制限はありません．)(重力を考えないとします．)

定常回転しているコマの縁を構成する物質は中心方向に向いた加速度を持ちます(速度の方向が変わることも速度変化＝加速度だからです)．

加速度を生むには力が必要ですので，中心方向に力が必要ですが，これは物体(ゴムでできたコマを考えるとわかります)が膨れないように引っ張る力として現れる張力が担います．そしてこの張力は全体として打ち消しあっているので，合力は0，さらに偶力もありません．つまりこの場合，張力がコマの(軸の)運動に影響を与えないのは，ご存じのことですね．

つぎに回転軸の方向が変化する場合を考えます．y軸周りに回転させましょう．このコマの軸は最初z軸にありますが，z軸からx軸に向きが変わるように一定の角速度でコマの軸が倒れていく状況を考えます．このときコマの縁を構成する物質はどのような加速度運動をするでしょうか?

このときコマの縁を構成する物質で重要なのは，xz平面に平行な速度ベクトルがあるような要素です．見ているあなたにとって，一番手前の部分と，一番奥の部分に当たります．まずは，手前だけ考えましょうか．

回転軸が60度に傾いている時を考えましょう(最初は90度とします)．このとき一番手前の部分は-30度の方向に速度ベクトルの方向がありますね．

ちょっと過去に戻りましょう．先ほどの要素は手前でなくなっているので速度ベクトルがxy平面からはずれますが無視します．

回転軸は 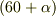$(60+\alpha)$ 度傾いているので，速度ベクトルは 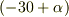$(-30+\alpha)$ 度の方向を向いています．(xy平面からはずれる向きは無視します)．

同様に，ちょっと未来にいきましょう．回転軸は 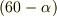$(60-\alpha)$ 度傾いているので，速度ベクトルは 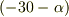$(-30-\alpha)$ 度の方向を向いています．

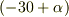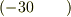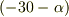速度ベクトルだけを紙面に書くと(始点をそろえます＝ホドグラフ)，速度ベクトルは 1. $(-30+\alpha)$ 度の方向 2. (-30~~~~~~ ) 度の方向 3. $(-30-\alpha)$ 度の方向と方向が変化しています．つまり加速度が発生します．この加速度の方向は回転軸に平行で原点に向いています．

今の話を奥の要素で考えると速度が逆なので，加速度は逆になります．(ホドグラフを書いて考えてください)

つまり手前の要素は原点方向に，奥の要素は原点から離れる方向に加速度，つまり，力が発生している事になります．これは回転軸を手前に倒すような回転を生む力(偶力)です．

以上をまとめると，＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊右ねじ回転しているコマの回転軸をxz平面内で負の回転をさせるには，コマには手前に倒すような回転を生む「偶力」が作用していなければいけない．(原点が固定されているので，「手前に向いた力が発生しなければいけない」でも良いです．) ＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊となります．コマの軸を動かす人は上の力の反作用を受けることになります．つまり，軸を動かすと直交している向きに力を受けることになります．

なお，力が掛からない状況なら軸の方向は変化できません．これが角運動量（の方向）の保存則です．

また，動きと力の関係の因果は逆でもかまいせん．これが，問題の状況になるわけです．

傾いた回転軸をさらに倒そうとする重力がかかると，コマの軸は予想される方向とは直交する方向に動きます．これは水平面内の回転になります．(章動と呼ばれる振動モードもありますが，ここでは考えません．)

これが歳差運動(ゴマ擦り運動)と呼ばれものです．

歳差運動が定常に行われている(章動がない)場合，重力はコマの要素の速度ベクトルの向きを変えることにすべて使われてしまいますので，軸を倒すことはありません．

これが何故回転しているコマが倒れないかの答えです．

# ある意味，「月は地球の重力を受けているのに，何故地面に落ちてこないのか?」という問いと似たような話(「重力が速度の方向変化に使われるから．」)です．

(正確には，釣り合いの議論ではなく，安定性の議論をしなければいけないですが，パスさせてください．)

Re: 自転車

小林＠那須さんのレス (2007/05/26(Sat) 21:00)

自転車と一輪車と独楽では準安定状態として立ち続ける理由が異なります．

自転車の場合は，自転車が傾くとハンドルが傾いたほうに自動的に切れるため倒れなくなります．ハンドルが切れるために，直進運動から円運動に変わります．円運動に変わることで，倒れない方向に遠心力が発生します．走る速度が小さくなると，ハンドルが切れても遠心力が発生しないので倒れやすくなります．

傾きに比例してハンドルが自動的に切れることは，「静止状態のままで自転車のサドルを手でもって傾けてやると，傾いた角度に比例してハンドルが切れる」ことを確認する実験で証明できます．ただし普通の地面では摩擦力が強すぎるので，前輪を水で塗らした鉄板等に乗せてやる必要があります．

傾きに比例してハンドルが切れる理由はフロント・フォークの形にあります．より具体的にはキャスター角とオフセットです．この二つを与えることで，自転車を傾けたとき，ハンドルを切った状態のほうが重力のポテンシャル・エネルギーが最小の状態になるからです．

車輪の角運動量で自転車が倒れないなどとする説明がありますが，こちらよりフォークのキャスター角とオフセットのほうが強く利いてきます．キャスター角とオフセットの設計を誤ると転倒しやすいバイクや自転車になってしまいます．逆に，車輪の質量がゼロで角運動量がない自転車が作れたとしても，走っていればキャスター角とオフセットによって自転車は倒れません．

ただし体重移動による自転車の方向制御には車輪の角運動量が利いてきます．自転車で右に曲がるためには重心を右に移すのですが，車輪の角運動量があるため反作用の利きが弱くなり重心移動がより効率的にできます．

Re: 自転車

私さんのレス (2007/05/26(Sat) 22:57)

みなさん大変ありがとうございます！！！

熟読＆理解中…

理解し終えたらまたレスを書きます．

Re: 自転車

yama さんのレス (2007/05/27(Sun) 00:49)

自転車の安定性はジャイロ効果もありますが，小林＠那須さんがおっしゃるようにハンドルが切れることが大きく影響しています．実際，ハンドルが切れないようにハンドルを固定してしまえば，よほどの高速で走らない限り簡単に倒れてしまうでしょう．ハンドルが切れることによる安定性は，キャスター角とオフセットに関係していることも小林＠那須さんがおっしゃるとおりで，キャスター角もオフセットも0なら車体が傾いてもハンドルは切れないでしょう．しかし，小林＠那須さんの説明では，車体が傾きハンドルが切れて円運動に移行した後どうなるのかという点の説明が不足しているように思います．傾いたまま円運動を続けるのではなく，前輪の接地点にはたらく摩擦力が傾いた車体を引き起こすと同時に切れたハンドルをもとに戻すことになると思います．このことはハンドルの回転軸のまわりの摩擦力のモーメントを考えれば分かるでしょう．

Re: 自転車

小林＠那須さんのレス (2007/05/27(Sun) 07:58)

yama さん，おはようございます．

>車体が傾きハンドルが切れて円運動に移行した後どうなるのか

私は，惰性で動いているとき：例えば自転車を手で押して無人で走らせているときに傾いたら，傾きに伴う倒す力と遠心力による起き上がる力が釣り合う状態での円運動を続けると思います．

後輪にトルクを与え加速させるときは自転車が起き上がってきます．バイクでクランクを高速に走り抜けるときに使うテクニックです．

砂地などでのように摩擦が大きくて定速度を保つためにトルクを与えつづけるときにどうなるかは，よく解りません．前輪のハブの摩擦を大きくしてやり定速度を保つためにトルクを与え続ける状態にしたときは，円運動を続けると思います．

Re: 自転車

zoro さんのレス (2007/05/27(Sun) 09:38)

私は，機械の構造を良く知りません．今回のスレッドで，２輪車では，自己安定性の論議には複雑な仕組みがある事を知りました．

他方，1輪車ではどうなるか知りたい所です．少なくとも，基本的な安定性の問題は1輪車でも，2輪車でも同一だろうと推察しています．とくに前進速度と垂直安定性との相関性は，1輪車の場合かなり大切だろうと感じます．

Re: 自転車

小林＠那須さんのレス (2007/05/27(Sun) 11:44)

>他方，1輪車ではどうなるか知りたい所です．

一輪車よりも単純な転がる輪を考えます．

転がる輪も重力により倒されます．ここで右に倒れたとして話を進めます．倒れながらも輪は前進します．前進すると右に倒れようとしていた輪は進行方向を右に代える回転の働きに変わります．これを続けると直線運動していた転がる輪は，回転運動しながら転がる輪になります．そして回転運動による遠心力と重力による倒れる力が釣り合うように，円を描きながら転がりつづけます．

>前進速度と垂直安定性

一輪車の前後方向の垂直安定性は，人間が前後方向の加速を制御することで実現していると考えます．人間が乗らない一輪車を手で押して走らせたとき，前後方向の垂直安定性を実現することは無理でしょう．

Re: 自転車

zoro さんのレス (2007/05/27(Sun) 12:01)

＞転がる輪も重力により倒されます．ここで右に倒れたとして話を進めます．

問題をこのように拡張されるのも良いですが，結局，「スピードが低いと不安定で，スピードを増すと安定するか」の回答にはなっていないようにおもいます．

ご指摘のように，自転車の車輪だけのケースを自分なりに検討してみたいとおもいます．

以上，ご返答，有り難うございました．

[home] [掲示板] [ページの先頭]