振動，エネルギーの減少

振動，エネルギーの減少

けん（大学2年） さんの書込 (2007/05/26(Sat) 00:12)

摩擦を受けながら振動する振動する質点の運動方程式を考える． m(d^2x/dt^2)=-kx-2mrdx/dt（m,k,rは正の定数） この場合にはE＝T＋Vは保存せずに時間とともに減少してゆく．

(a)dE/dt＝-4rT が成立することを運動方程式を用いることで示せ．

(b)摩擦が十分小さいときは，(a)の関係式の時間平均をとることで，近似的にエネルギーの時間平均に対する変化の様子を求めることができる．〈T〉＝（E）/2とおいて，（E）に対する微分方程式を作り，その解を求めよ． ただし，（T）＝（1/Δ）∫(tからt＋Δまで)T(t)dt （E）＝（1/Δ）∫(tからt＋Δまで)E(t)dt とする．

(b)で，（dE/dt）＝-2r（E）となります． （dE/dt）＝d（E）/dtとして，（E）に対する微分方程式を導くのですが，（dE/dt）＝d（E）/dtはどうして成立するのでしょうか．よろしくお願いします．

Re: 振動，エネルギーの減少

toorisugari no Hiro さんのレス (2007/05/26(Sat) 01:48)

TやEの定義がよくわかりません．完全に問題を書いてくださいね．(今回の質問には影響ないけど)．

> （dE/dt）＝d（E）/dtとして，（E）に対する微分方程式を導くのですが，（dE/dt）＝d（E）/dtはどうして成立するのでしょうか．

微分と積分が交換するからです．

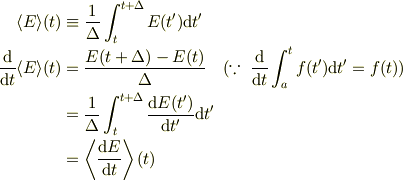
\langle E \rangle (t) &\equiv \frac{1}{\Delta}\int^{t + \Delta }_{t}E(t')\mathrm{d}t'\\\frac{\mathrm{d}}{\mathrm{d}t}\langle E \rangle (t) &= \frac{E(t + \Delta)-E(t)}{\Delta}\quad(\because~ \frac{\mathrm{d}}{\mathrm{d}t}\int_{a}^{t}f(t')\mathrm{d}t'=f(t))\\&= \frac{1}{\Delta}\int^{t + \Delta}_{t}\frac{\mathrm{d}E(t')}{\mathrm{d}t'}\mathrm{d}t'\\&= \left\langle \frac{\mathrm{d}E}{\mathrm{d}t} \right\rangle (t)

Re: 振動，エネルギーの減少

けん（大学2年） さんのレス (2007/05/26(Sat) 02:13)

ありがとうございます．

Δの定義を書き忘れていました．すみません． Δ＝2π√(m/k)でした．

Re: 振動，エネルギーの減少

toorisugari no Hiro さんのレス (2007/05/26(Sat) 02:36)

どういう意図の問題か見えませんが(普通に微分方程式を解いた方が早い．非線形方程式でも解くのだろうか?)，この手の問題を解くときは最低でも係数は整理して，

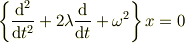
\left\{\frac{\mathrm{d}^2}{\mathrm{d}t^2}+2\lambda\frac{\mathrm{d}}{\mathrm{d}t}+\omega^2\right\}x =0

とすべきです．できれば，時間とパラメータも無次元化して，

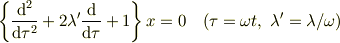
\left\{\frac{\mathrm{d}^2}{\mathrm{d}\tau^2}+2\lambda'\frac{\mathrm{d}}{\mathrm{d}\tau}+1\right\}x &=0\quad(\tau =\omega t, ~\lambda'=\lambda/\omega)

とした方が計算の見通しが良いです( 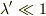\lambda'\ll 1 とできる)．なおこの時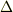， \Delta ，あるいはだいたいの周期は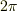， 2\pi になります．

Re: 振動，エネルギーの減少

けん（大学2年） さんのレス (2007/05/26(Sat) 02:46)

おそらく，微分方程式を解かなくても近似的にはエネルギーの減り方が分かるというのが意図の問題だと思います．

なぜλ'<<1とできるのですか？λ<<ωの場合のことですか？

Re: 振動，エネルギーの減少

toorisugari no Hiro さんのレス (2007/05/26(Sat) 02:55)

> おそらく，微分方程式を解かなくても近似的にはエネルギーの減り方が分かるというのが意図の問題だと思います．

単振動を解くコストがいることをお忘れなく．このコストは普通に微分方程式を解くのと変わりません．(ま，ここで言うことではないですね．)

> なぜλ'<<1とできるのですか？λ<<ωの場合のことですか？

そうです．

> 摩擦が十分小さいときは

何に比べて小さいかをいっていないですね．復元力に対してとか比較の対象が必要です．同じ次元の量で比べなければいけないので 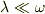\lambda\ll\omega が条件のはずです．

この話は遅い時間変化と速い時間変化の分離という物理の重要な手法(摂動論)につながっていきます．よく勉強しておいてください．

Re: 振動，エネルギーの減少

なんとなく さんのレス (2007/05/26(Sat) 13:18)

横やりすみませんが，(a)は解決したのですか？ もし，まだなら，これはよくあるエネルギー（第一）積分の形にすれば良いだけですので，与式の両辺にdx/dtをかけて整理すればいいんじゃないですか． 微分方程式は仰るとおり，解く必要はないと思いますよ．

Re: 振動，エネルギーの減少

けん（大学2年） さんのレス (2007/05/30(Wed) 23:09)

お返事遅れてすみません．

＞toorisugari no Hiroさん

よく勉強しておきます．どうもありがとうございました．

＞なんとなくさん

横やりなんて仰らずに何でも書き込んで下さい． aは解決しました．ありがとうございました．