物理化学？

内部エネルギーの増加は ΔＥ＝Ｑ＋Ｗです．Ｑは外部から加えられた熱量です．Ｗは外部からされた仕事ですので体積変化をΔＶとしますとＷ＝−ＰΔＶとなります．比熱はＱ／ΔＴですので定積比熱Ｃｖ＝ΔＥ／ΔＴ定圧比熱Ｃｐ＝ΔＥ／ΔＴ＋ＰΔＶ／ΔＴ＝Ｃｖ＋ＰΔＶ／ΔＴです．圧力一定の時はＰΔＶ／ΔＴ＝Δ（ＰＶ）／ΔＴ＝Δ（ＲＴ）／ΔＴ＝Ｒです．１原子分子の場合，Ｅ＝３ＲＴ／２は気体分子運動論から出します．この式を１自由度当たりＲＴ／２と読んでエネルギー等配分則を導きます．２原子分子の場合原子間距離が変わらないという仮定で自由度を５とするとＥ＝５ＲＴ／２が出てきます．Ｃｖ＝ΔＥ／ΔＴ＝５Ｒ／２となります．

ここまでは高等学校の教科書に載っています．（「エネルギー等配分則」という言葉は出てこないと思います．むしろ温度がうんどうエネルギーの尺度になっているということにウエイトがあるようです．）

２原子分子の伸縮振動はもっと高い温度での励起になりますので通常の温度では結合距離が変わらないと考えています．分子によって起こりやすさに差がありますので比熱の実測値は５Ｒ／２から少しずれます．

Re: 物理化学？

なんとなくさんのレス (2007/05/17(Thu) 13:26)

こんにちは．横やりすみません．余計なことかも知れませんが，かなり初等的なところでつまずいているように見受けられます．本当に余計なら，以下は無視してください．問題の意図する前提条件にはkomagatakeさんの言われるように圧力（気圧）が不足しています．部屋なので1気圧（標準大気圧）とするのでしょう．すると，この問題はどのような道筋で考えればよいのか，例を示しますので，参考にしてください．部屋には空気があって，酸素や窒素があるでしょうが，まあ，理想気体と見なすのでしょう．理想気体で考える場合，1モル（分子量）は空気の分子量に換算する必要がありますが，体積なら差が無いですね．理想気体は暗黙に，０℃1気圧で1モルが22.4リットルを占めるというお約束ですが，今は１０℃ですから，この部屋4×4×3(ｍ3)の空気は何モルあるか計算できます．部屋に空気や熱の出入りが無いとすると，体積一定ですから，定積モル比熱を使えば必要な熱量が計算できそうです．定積モル比熱は1モルの気体を体積一定で１°K上げるのに必要な熱量ですから，上記モル数分，25-10=15(°K)上げるのは？ここで，温度でモル数は変化しないことを使っています．そんなことは分かっている！ということなら，失礼しました．

Re: 物理化学？

ｙama さんのレス (2007/05/17(Thu) 14:56)

部屋が密閉されていれば，モル数は変わりませんが，実際には窓や扉には隙間があって空気が出入りし，外部の気圧に等しくなるのではないでしょうか．その場合は，体積と圧力が一定でモル数が変化することになりますね．しかしそうなると問題が難しくなるので，気密室のようなものが想定されているのかもしれません．両方の場合を考えてみるのもいいと思います．

Re: 物理化学？

あやこさんのレス (2007/05/17(Thu) 15:53)

皆さんありがとうございます．皆さんのヒントをもとに自分なりに考えてみました．間違っていたら指摘していただけるとうれしいです． 1アトム，10℃と想定してｎ＝[１atm*48ｍ3]／[8.31＊10-3乗(ｍ3・atm/K・mol)*(273+10)(K)]＝20.41mol Ｃｖ＝５/２Ｒ＝２０．７８(Ｊ・Ｋ-1・mol-1）求める値を?Ｕとすると?Ｔ＝１５Ｋより ?Ｕ＝２０．４１＊２０．７８＊１５＝６３６１．７９７（Ｊ）

Re: 物理化学？

ｋｏｍａｇａｔａｋｅさんのレス (2007/05/17(Thu) 19:09)

あやこさん

＞ｎ＝[１atm*48ｍ3]／[8.31＊10-3乗(ｍ3・atm/K・mol)*(273+10)(K)]＝20.41mol ＞Ｃｖ＝５/２Ｒ＝２０．７８(Ｊ・Ｋ-1・mol-1）

２行目でＲ＝８．３１Ｊ／Ｋ・ｍｏｌを使っています．１行目での値がこの値を換算したものになっていません．桁が違っています．

概算をしてみると間違いが分かります．状態方程式に振り回されるといけません．１ａｔｍ，１０℃で４８ｍ＾３の空気ですね．２７３Ｋと２８３Ｋはあまり違いはありません．４８×１０＾３／２２．４と近いはずです．これは２０００のオーダーです．１００倍違ってきています．

Re: 物理化学？

あやこさんのレス (2007/05/17(Thu) 20:09)

>２行目でＲ＝８．３１Ｊ／Ｋ・ｍｏｌを使っています．１行目での値がこの値を換算したものになっていません．桁が違っています．

ｎ＝[１atm*48ｍ3]／[8.21＊10-2乗(dｍ3・atm/K・mol)*(273+10)(K)]とし，ｄは１０の-１乗だから，ｎ＝２０６５．９１molとすればよいのでしょうか？お願いします．

Re: 物理化学？

ｋｏｍａｇａｔａｋｅさんのレス (2007/05/17(Thu) 23:37)

いいと思います．ただこんなに桁数をたくさんにする必要はないと思います．２０６５．９１は多すぎます．せいぜい２桁というところだと思います．最後の結果も同様です．

Re: 物理化学？

あやこさんのレス (2007/05/18(Fri) 05:39)

わかりました．本当にありがとうございます！

Re: 物理化学？

ｋｏｍａｇａｔａｋｅさんのレス (2007/05/18(Fri) 15:37)

ｙａｍａさんからの宿題について

部屋から空気がもれてＰ一定になっている場合

難しいことは忘れましたので初等的に解いてみました．間違っているかも知れません．

ピストンの付いたシリンダーの中に気体が入っているとします．温度，圧力，体積をＴ，Ｐ，Ｖとします．外部の圧力もＰとします．ＰＶ＝ｎＲＴです．

ＴをＴ’まで加熱します．（１）ピストンが固定されているとＱ＝ｎＣｖ（Ｔ’−Ｔ）です．（２）ピストンが自由に動くことが出来るときはＱ＝ｎＣｐ（Ｔ’−Ｔ）です．

（３）ピストンに穴があって中の空気が絶えず外の広い空間にもれているときは？

膨張がありますので定圧比熱が必要でしょうが（２）とは違います．出て行った空気はもう暖める必要がないので（２）より少なくなるはずです．そこで次のように考えました．二重のピストンを考えます．内側のピストンは固定されています．外側のピストンは自由に動くことが出来ます．内側のピストンにはには穴が空いています．はじめ２つのピストンは密着しています．温度を少し（δＴ）だけ上げると膨張して外のピストンが動きます．釣り合った状態での体積はＶ＋δＶ＝ｎＲ（Ｔ＋δＴ）で決まります．この時の熱量はｎＣｐδＴです．ここでδＶの空気を捨てます．物質量はｎＶ／（Ｖ＋δＶ）＝ｎＴ／（Ｔ＋δＴ）に減ってしまいます．この空気の温度をまたδＴだけ上げます．必要な熱量はｎＴ／（Ｔ＋δＴ）ＣｐδＴになります．これを繰り返して和を取ると必要な熱量になると思います．

Ｔ＝２８３Ｋ，Ｔ’＝２９８Ｋで１Ｋ刻みで和を取るとＱ＝ｎＣｐ（Ｔ’−Ｔ）×０．８８となりました．Ｃｖ＝Ｃｐ×（５／７）＝Ｃｐ×０．７１ですからほぼ（１）と（２）の中間の値です．

これでいいでしょうか．

Re: 物理化学？

ｙama さんのレス (2007/05/18(Fri) 18:12)

考え方はいいと思いますが，計算結果は違っているように思います．最終的に外部に出て行く空気量は初めの空気量の５％程度なので，少なく見積もってもＱ＝ｎＣｐ（Ｔ’−Ｔ）×0,95 程度にはなるはずです．

きちんと計算すると

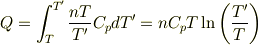
$Q=\int_T^{T'}\frac{nT}{T'}C_pdT'=nC_pT\ln\left(\frac{T'}{T}\right)$

となりますが，これはほぼＱ＝ｎＣｐ（Ｔ’−Ｔ）×0,97 になると思います．

Re: 物理化学？

ｋｏｍａｇａｔａｋｅさんのレス (2007/05/18(Fri) 19:27)

ｙａｍａさん

私もはじめはｌｏｇの形になるのかなと思ってやり始めました．でも簡単な積分の形になりませんでした．

違いがどこにあるかの吟味がちょっと難しいのですがとにかく書いてみます．

Ｎｏ１５９２８に１項目と２項目とを書きました．多分その次に違いがあると思います．１項目ｎＣｐδＴ２項目ｎＴ／（Ｔ＋δＴ）ＣｐδＴ３項目ｎＴ＾２／（Ｔ＋δＴ）（Ｔ＋２δＴ）ＣｐδＴ４項目ｎＴ＾３／［（Ｔ＋δＴ）（Ｔ＋２δＴ）（Ｔ＋３δＴ）ＣｐδＴ・・・・

お示しの積分はＴ／Ｔ’の形になっていますので違いがあります．これは各区切りごとに膨張した空気を捨てていくということでその分の加熱が不要になっている分熱量が少なくなっていると考えられます．

Ｑ＝ｎＣｐ（Ｔ’−Ｔ）×０．９５

について考えてみました．最終的に空気が５％減少したとしたときの見積もりです．

ｎＣｐ（Ｔ’−Ｔ）は空気を全て加熱した時のものです．０．９５をかけるということで最後に一度に捨てるということと同じだと見ていることになります．残った空気に相当する分の熱量を割合で求めています．捨てる部分にも熱を加えていることになっていますので必要な熱量が大きくなってしまったのではないでしょうか．

私の出した式は簡単な積分に直せませんでしたので和を求めました．

Re: 物理化学？

yama さんのレス (2007/05/18(Fri) 22:44)

３項目からが違っているように思います．３項目は，２項目に（Ｔ＋δＴ）／（Ｔ＋２δＴ）を掛けたものになるので，ｎＴ／（Ｔ＋２δＴ）ＣｐδＴになり，同様に４項目はｎＴ／（Ｔ＋３δＴ）ＣｐδＴになります． δＴを限りなく小さくすると，これらの項の総和は前記の積分に等しくなります．

また，最終的には 95％程度すなわち物質量で 0.95ｎ程度の空気が残るわけです．この空気を一定圧力下で温度ＴからＴ’まで加熱するのに必要な熱量がＱ＝ｎＣｐ（Ｔ’−Ｔ）×0,95 になるわけです．つまり，これは最終的に残る空気だけを加熱する場合の熱量なので，捨てられる空気を加熱する熱量は含まれていません．実際には捨てられる空気も多少は加熱されるので，熱量はこれより多くなります．「少なく見積もっても」この程度にはなるということです．

Re: 物理化学？

ｋｏｍａｇａｔａｋｅさんのレス (2007/05/19(Sat) 07:04)

ｙａｍａさん

計算をやりなおしました．途中の変形に間違いが見つかりました．

ありがとうございました．

[home] [掲示板] [ページの先頭]