電位の求め方
電位の求め方
tip★ さんの書込 (2007/05/16(Wed) 20:41)
2本の平行直線上に正負の電荷（±ρ[C/m]）が一様に分布している系のクーロン場について，直線に垂直な断面の無限に広い平面上でのPの電位を求めよ． ただし，＋ρの電荷からPまでの距離をr1,−ρの電荷からPまでの距離をr2である．
|――――――――――――――｜ |｜ |・P ｜ |｜ |＋ρ[C/m]−ρ[C/m]| |●○｜ |｜ |｜ |｜ |――――――――――――――｜ 上から見た図
まずは，−ρの電荷を無視して，＋ρの電荷のほうだけ考える． ＋ρの直線を中心軸として，半径r，高さ１の円柱をについてガウスの法則を適用すると ∬E・n dS ＝∫ρ/ε(0)dl Eは電界（ベクトル），ｎは法線ベクトル，ρは線電荷密度，ε(0)は真空の誘電率 を使うと， （左辺）＝2πr×1×|E| （右辺）＝（ρ×1）/ε(0) よって，|E|＝ρ/2πrε(0) [V/m] 電界の方向は，中心軸から外側に放射状である．
−ρの電荷のほうについても同様にすると |E|＝ρ/2πrε(0) [V/m] 電界の方向は，＋ρの逆である．（なんて表現したらいいのわかりません．）
V＝−∫E・drなので
V＝−∫(ρ/2πrε(0))dr (積分範囲：0からr1)＋∫(ρ/2πrε(0))dr（0からr2） ＝−{ρ/2πε(0)}log(r1)＋{ρ/2πε(0)}log(r2) ＝{ρ/2πε(0)}log(r2/r1) [V]
このようになりました．
友達の計算結果は{ρ/4πε(0)}log(r2/r1) [V] になっていたのですが，どっちが正しいでしょうか？
よろしくお願いします．
Re: 電位の求め方
toorisugari no Hiro さんのレス (2007/05/16(Wed) 21:07)
> どっちが正しいでしょう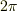か？
か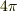 
かということなら，2次元ですし，tip★さんが正しいと思います．
Re: 電位の求め方
tip★ さんのレス (2007/05/16(Wed) 21:18)
>>toorisugari no Hiro
ありがとうございます． toorisugari no Hiroさんならどのようにして解きますか？ 参考にしたいのですが・・・
よろしくお願いします．
