量子力学について
量子力学について
はらだ さんの書込 (2007/05/16(Wed) 12:54)
こんにちは,大学生のはらだと申します. 量子力学でわからない問題があります. よろしくお願いします.
^←Aの上に^がついています. <(ΔA)^2>≧0を示せ. ↑ 2乗です.
Texの書き方がよくわからなかったのでこの書き方になりました.
わかりにくくてすみません.
Re: 量子力学について
Re: 量子力学について
はらだ さんのレス (2007/05/16(Wed) 14:19)
ありがとうございます. 確かにエルミート演算子なのですが・・・ すみません...考えてみたのですが,わかりませんでした・・・
Re: 量子力学について
toorisugari no Hiro さんのレス (2007/05/16(Wed) 16:50)
> わかりませんでした・・・
どこまで理解していて,どこからわかりませんか?
この問題を解くための,予備知識をどれくらい理解しているのか教えてください. (講義でどのようなことを習ったか?それをどの程度理解してるか?)
# すべてわからないと言うことなら,教えようがありません.
Re: 量子力学について
はらだ さんのレス (2007/05/16(Wed) 17:29)
エルミート演算子は習ったのですが, これを,どう証明したらいいのかがイマイチわかりません.
不確定性関係と交換関係の分散を使えばいいのでしょうか・・・ 色々自分なりに調べてみたのですが・・・ どうも量子力学が苦手で...すみません...
Re: 量子力学について
toorisugari no Hiro さんのレス (2007/05/16(Wed) 17:38)
> エルミート演算子は習ったのですが,
エルミート演算子の定義を教えてください.あと,期待値 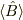 の(数学的な)定義も教えてください.
の(数学的な)定義も教えてください.
> 不確定性関係と交換関係の分散を使えばいいのでしょうか・・・
いいえ.それ以前の「すうがく」です.
対称行列
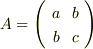 があるとき,任意のベクトル
があるとき,任意のベクトル 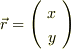 に対して
に対して
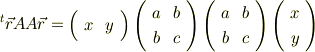
は正また0です.(確かめて見てください.判別式か完全平方に持ち込めばいいですね.)
2×2だけでなくn×nの対称行列でも同様のことが言えるというのが,ほぼ題意になります(複素無限次元ベクトルであることがやっかいですが).この証明をうっとうしい計算をしないで証明する方法があります.
Re: 量子力学について
はらだ さんのレス (2007/05/16(Wed) 18:55)
少し,言われている意味がわかってきた気がします. ありがとうございます. もう少し,考えてみたいと思います.
Re: 量子力学について
はらだ さんのレス (2007/05/16(Wed) 19:14)
うっとうしい計算をしないで証明する方法があるんですか・・・!?
Re: 量子力学について
toorisugari no Hiro さんのレス (2007/05/16(Wed) 19:28)
> うっとうしい計算をしないで証明する方法があるんですか・・・!?
ええ.でも,まず,2×2をうっとうしい計算で証明してみないとありがたさはわからないかな?
証明法を説明するには,
>> エルミート演算子の定義を教えてください.あと,期待値 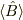 の(数学的な)定義も教えてください.
の(数学的な)定義も教えてください.
に答えて欲しいです.
Re: 量子力学について
はらだ さんのレス (2007/05/16(Wed) 20:43)
エルミートの定義って・・・ エルミート作用素の固有値は必ず実数であり, また,相異なる固有値に属する固有ベクトル同士は直交している.
- 期待値B
- ^
<b|B|b>=b<b|b>=b*<b|b>
よって,(b−b*)<b|b>=0
違いますでしょうか・・・
Re: 量子力学について
toorisugari no Hiro さんのレス (2007/05/16(Wed) 21:02)
> エルミートの定義って・・・ > エルミート作用素の固有値は必ず実数であり, > また,相異なる固有値に属する固有ベクトル同士は直交している.
えーっと.これでもいいんですが^^; エルミート共役をご存じですか?
> 期待値B > ^ > <b|B|b>=b<b|b>=b*<b|b> > よって,(b−b*)<b|b>=0
これは > エルミート作用素の固有値は必ず実数であり, の証明ですが...
# 欲しいのは <b|B|b>だけだったりする.
# ただし 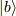 は
は 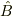 の固有ベクトルである必要はありません.
の固有ベクトルである必要はありません.
Re: 量子力学について
はらだ さんのレス (2007/05/16(Wed) 21:09)
> 欲しいのは <b|B|b>だけだったりする
そうなんですか!? もっと勉強が必要ですね... でも,少しずつわかってきたような気がします.
Re: 量子力学について
はらだ さんのレス (2007/05/16(Wed) 21:10)
ちなみに,タイムリミットは・・・ 明日提出なんです・・・
Re: 量子力学について
はらだ さんのレス (2007/05/16(Wed) 21:19)
はい,何とか今日中にできるようにしたいです.
エルミート共役・・・_ αをエルミート共役とおいたとき,αと表せれますよね・・・ 行列で表すと複素共役をとってさらに転置するやつですよね・・・
Re: 量子力学について
はらだ さんのレス (2007/05/16(Wed) 21:23)
すみません・・・αの上に_がきます・・・ ずれてしまいました...
Re: 量子力学について
toorisugari no Hiro さんのレス (2007/05/16(Wed) 21:54)
> 行列で表すと複素共役をとってさらに転置するやつですよね・・・
そうですね.ですからエルミート演算子は「複素共役をとってさらに転置」しても変わらないものですね.つまり,対称行列の特別版(拡張版?)なわけです.
ところで,転置行列の「高級」な定義はわかりますか?
「
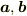 を実ベクトル空間の任意の元とする.行列
を実ベクトル空間の任意の元とする.行列 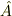 の転置行列とは,
の転置行列とは, 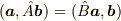 を満たす
を満たす 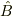 のことである.これを
のことである.これを 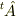 と呼ぶ.
」
と呼ぶ.
」
これがわかれば,以下のことが理解できると思います. 実ベクトル空間と対称行列で考えましょう.
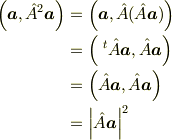
これが問題とつながれば,理解したことになるんですが....
先の2x2問題ならこう考えてもいいですね.
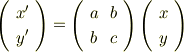
と置くとこのベクトルの転置は
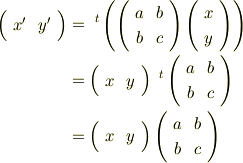
となります.「証明」は
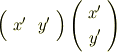
が非負であることを示せばいいことになります.
Re: 量子力学について
はらだ さんのレス (2007/05/16(Wed) 22:05)
あっ,少し,わかってきた気がします. もう少し,考えてみます. もう一度,じっくり考えるとわかるような感じがしてきました.
Re: 量子力学について
toorisugari no Hiro さんのレス (2007/05/16(Wed) 22:11)
> あっ,少し,わかってきた気がします.
よかった.もう少しですからがんばってください. 私も締め切り抱えているので,ここまでにさせてください.
Re: 量子力学について
はらだ さんのレス (2007/05/16(Wed) 22:14)
すみません. 本当にありがとうございました. 何とか,がんばって答えだせるようにしたいです.
Re: 量子力学について
はらだ さんのレス (2007/05/16(Wed) 22:42)
toorisugari no Hiroさん
本当にありがとうございました. 何とか,できました.たぶん大丈夫だと思います. これは,数学なんですね.
なんかすっきりした感じがします. 大切なお時間をいただきありがとうございました.
Re: 量子力学について
toorisugari no Hiro さんのレス (2007/05/16(Wed) 22:57)
> 何とか,できました.
おめでとうございます.
> これは,数学なんですね.
そです.でも,これは量子力学でたびたび出てくる重要事項です.
> たぶん大丈夫だと思います.
はらださんなりの解答を書いてもらえれば,きっとどなたかが添削してくれると思いますよ.
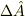 がエルミート演算子ということなら
がエルミート演算子ということなら