電位差

キャロットさんの書込 (2007/05/14(Mon) 21:18)

原点に置かれた点電荷ＱによるＸＹ平面状におけるＡ(2,2)とＢ(4,4)との間の電位差φ_BA=-∫Ｅ・ｄｓを次の二つの直線経路で求めよ． 1, ↑積分範囲はＡからＢＡ(2,2)→Ｃ(4,2)→Ｂ(4,4) ２Ａ(2,2)→Ｂ(4,4) という問題なのですがどう解いたらいいかわからなくて困ってます．だれかアドバイスお願いします

Re: 電位差

zoro さんのレス (2007/05/15(Tue) 05:42)

キャロットさん，少なくとも大学の電磁気の問題と仮定して，ヒントを書きます

題意より原点に電荷Qが置かれていて，その平面は真空中とすれば，電場についてのクーロンの法則が成立します．また，電場と静電ポテンシャルとの関係も与えられているとします．

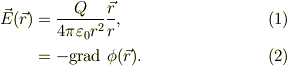
$\vec E(\vec r) &= \frac{Q}{4\pi \varepsilon_{0}r^{2}}\frac{\vec r}{r}, \tag{1}\\&= -\mbox{grad}\ \phi(\vec r). \tag{2}$

2点間の静電ポテンシャルの関係を整理して，式(2)を使うと

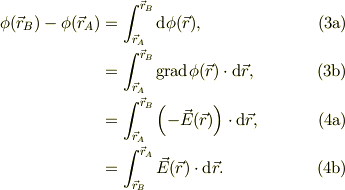
$\phi(\vec r_{B}) -\phi(\vec r_{A}) &= \int_{\vec r_{A}}^{\vec r_{B}}\mbox{d}\phi(\vec r), \tag{3a}\\&= \int_{\vec r_{A}}^{\vec r_{B}}\mbox{grad}\phi(\vec r)\cdot \mbox{d}\vec r, \tag{3b}\\&= \int_{\vec r_{A}}^{\vec r_{B}}\left( -\vec E(\vec r) \right) \cdot \mbox{d}\vec r, \tag{4a}\\&= \int_{\vec r_{B}}^{\vec r_{A}}\vec E(\vec r) \cdot \mbox{d}\vec r. \tag{4b}$

解らない点は質問して下さいね．

Re: 電位差

キャロットさんのレス (2007/05/15(Tue) 15:44)

Ａ→Ｃ rーr_i=ocーOA=2i

Ｃ→Ｂ

rーr_i=OBーOC=2j のように考えてそれぞれ考えたのですが経路によって値が変わってしまってできませんf^_^;どのようにしたらいいのでしょうか？

Re: 電位差

zoro さんのレス (2007/05/15(Tue) 17:54)

お書きになっている式；

＞Ａ→Ｃ＞rーr_i=ocーOA=2i

や

＞Ｃ→Ｂ＞＞rーr_i=OBーOC=2j

の意味がわかりません．恐らく，A点からx軸に沿ってC点まで線積分した値と，C点からy軸に沿ってB点まで線積分した値とを出されようとしているように推測しますが...．

もし，お使いの教科書がなにか判れば，図書館で借りて見ますがどうでしょうか．

Re: 電位差

zoro さんのレス (2007/05/15(Tue) 18:42)

お書きになったのは，座標の差分値みたいなものですか．

<pre>

+y軸<b>j</b> ↑ ｜｜B(4,4) ＋・｜／｜／｜／｜／＋・・｜A(2,2)C(4,2) ｜｜｜＋ーーーー＋ーーーー＋ーーーーー→ x軸<b>i</b> O(0,0)

</pre>

従って， (x,y) の２次元ベクトルを考えると；

$\vec r &= x\bm{i} +y\bm{j}\\r^{2} &= x^{2}+y^{2}$

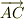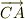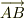積分経路は2つを比較；（１） $\overrightarrow{AC}$ と $\overrightarrow{CA}$ （２） $\overrightarrow{AB}$ ：斜め

を別々に計算したい，とか？

Re: 電位差

なんとなくさんのレス (2007/05/16(Wed) 11:44)

横やり失礼します． zoroさんの「教育的配慮」かとも思ったのですが，題意は明らかですし，質問者も分かっているようですので，別なヒントを出します． ∫E・ds において，A→C（dx,y=2)，C→B（dy,x=4)，とXY座標で計算し和を取る, もう一つの経路は，A→B（dr)と極座標で計算すればいいでしょう．ここで，dx,dy,drはそれぞれdsにあたります．Eとの内積に注意しましょう．それだけです．

Re: 電位差

キャロットさんのレス (2007/05/17(Thu) 22:16)

つまり， ∫E・ds=∫{(1/4πε)Q(xi+2j)/r^3}・idx =(1/4πε)Q∫{x/(x^2+2^2)^(3/2)}dx =(1/4πε)Q∫{t^(-3/2)・(1/2)}dt として解いていくということですよね？

Re: 電位差

zoro さんのレス (2007/05/17(Thu) 23:04)

だとおもいます．次にjdyの積分をして足すのですね．

たほう斜めの積分も別途して，上の結果と付き合わせて下さい．

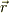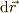この場合， $\vec r$ と $\mbox{d}\vec r$ とは並行であるので，

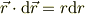
$\vec r \cdot \mbox{d}\vec r = r\mbox{d}r$

という，劇的な状況になります．

Re: 電位差

キャロットさんのレス (2007/05/18(Fri) 14:20)

わかりました！どうもありがとうございました．

Re: 電位差

zoro さんのレス (2007/05/20(Sun) 13:28)

この問題は，静電気や重力のポテンシャルでの典型的な問題とおもいます．そこで，すこし，補足説明をしておきます．

簡単の為に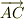， $\overrightarrow{AC}$ の計算だけに着目します．すなわち；

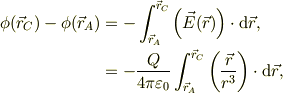
$\phi(\vec r_{C}) -\phi(\vec r_{A}) &= -\int_{\vec r_{A}}^{\vec r_{C}}\left( \vec E(\vec r) \right) \cdot \mbox{d}\vec r,\\&= -\frac{Q}{4\pi \varepsilon_{0}}\int_{\vec r_{A}}^{\vec r_{C}}\left( \frac{\vec r}{r^{3}} \right) \cdot \mbox{d}\vec r,$

を求めるのが問題です．そこで，すこし遠廻りですが，点AとCとの位置と原点からの距離とを変数にしておきます．

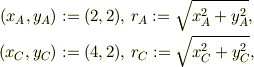
$(x_{A},y_{A}) := (2,2),\ & r_{A}:=\sqrt{x_{A}^{2} +y_{A}^{2}}, \\(x_{C},y_{C}) := (4,2),\ & r_{C}:=\sqrt{x_{C}^{2} +y_{C}^{2}},$

式(1)の積分部分を考えると,この領域では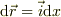， $\mbox{d}\vec r= \vec i \mbox{d}x$ だから，

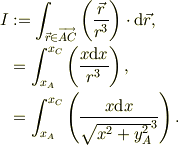
$I &:=\int_{\vec r \in \overrightarrow{AC}}\left( \frac{\vec r}{r^{3}} \right) \cdot \mbox{d}\vec r, \\ &= \int_{x_{A}}^{x_{C}}\left( \frac{x\mbox{d}x}{r^{3}} \right),\\&= \int_{x_{A}}^{x_{C}}\left( \frac{x\mbox{d}x}{\sqrt{x^2+y_{A}^2}^{3}} \right).$

ここで，変数変換，

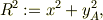
とすれば，その微分は；

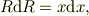
$R\mbox{d}R =x\mbox{d}x,$

だから，

$I &= \int_{x_{A}}^{x_{C}}\frac{x\mbox{d}x}{r^{3}},\\&= \int_{r_{A}}^{r_{C}}\frac{R\mbox{d}R}{R^{3}},\\&= \left[ -R^{-1}\right]_{R=r_{A}}^{R=r_{C}},\\&= -\left( \frac{1}{r_{C}}-\frac{1}{r_{A}} \right).$

もどって，

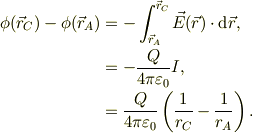
$\phi(\vec r_{C}) -\phi(\vec r_{A}) &= -\int_{\vec r_{A}}^{\vec r_{C}} \vec E(\vec r) \cdot \mbox{d}\vec r,\\&= -\frac{Q}{4\pi \varepsilon_{0}}I,\\&= \frac{Q}{4\pi \varepsilon_{0}}\left( \frac{1}{r_{C}}-\frac{1}{r_{A}} \right).$

となります．味噌は，x軸の積分をしたのに，結果は開始点，終了点の原点からの距離だけで表せられた事ですね．同様に考えると，どの積分も同じですから...．

結局，ベクトル解析は，この事を如何に一般的に表すかという為に進歩したと考えることも可能だと思います．

あとは言わずもがな．それにしても，中心力とは面白いものですね．

[home] [掲示板] [ページの先頭]