時速を秒速に直す公式
時速を秒速に直す公式
netwire さんの書込 (2007/05/12(Sat) 12:54)
高2で物理Iを学習している者です.疑問に思ったことがあるので質問させてください. 時速〔km/h〕を秒速〔m/s〕に直すには,1000/3600を時速に掛ければよいということは分かるのですが, 時速〔km/h〕を秒速〔m/s〕に直す公式というものは,どのように定義されているのでしょうか. □や△などといった記号を使った式は,小学生のころに見た覚えがありますが, vやtなどといった文字を使った式は見たことがありません.
Re: 時速を秒速に直す公式
yama さんのレス (2007/05/12(Sat) 15:34)
「時速〔km/h〕を秒速〔m/s〕に直すには,1000/3600を時速に掛ければよい」
ということは逆に
「秒速〔m/s〕を時速〔km/h〕に直すには,1000/3600で秒速を割ればよい(つまり3.6倍すればよい)」
ということになると思います.これは定義ではなく,数学的な結論です. あるいは
1m/s=3600m/3600s=3.6km/1h=3.6km/h
としてもいいでしょう.
Re: 時速を秒速に直す公式
zoro さんのレス (2007/05/12(Sat) 16:33)
netwireさん,
問題を,yamaさんが推測された;
「秒速〔m/s〕を時速〔km/h〕に直すには」として,自分の方法を記します.
1m/s = (1km/1000)/(1h/3600) = 3600/1000 km/h = 3.6km/h
というのは如何でしょうか?
#私は,今年度の高校の物理の教科書を幾つか購入しましたが,最近の教科書では,大学等で使っているように,「数値」と「単位」を区別しないで書いているようです.すなわち単位部を「[ ]」で囲わないようです.如何ですか,識者の皆様?
Re: 時速を秒速に直す公式
netwire さんのレス (2007/05/12(Sat) 18:02)
yamaさん,zoroさん,回答ありがとうございます. 特別に公式が定義されているわけではないのですね.
ちなみに私が使っている教科書(第一学習社)では,数値に付ける単位は括弧で囲まず, 文字に付ける単位は亀甲括弧〔〕で囲んであります. 例 t〔s〕 v〔m/s〕 10s 9.0m/s
Re: 時速を秒速に直す公式
zoro さんのレス (2007/05/12(Sat) 18:16)
netwireさん,
>数値に付ける単位は括弧で囲まず, >文字に付ける単位は亀甲括弧〔〕で囲んであります.
情報有り難うございます.亀甲括弧〔〕というのは初めて知りました.今,自分の所にいないので帰宅後に,購入した教科書を眺めてみます(笑).
Re: 時速を秒速に直す公式
yama さんのレス (2007/05/12(Sat) 22:17)
質問を勘違いしていたようです. 「時速〔km/h〕を秒速〔m/s〕に直すには,1000/3600を時速に掛ければよい」のはなぜかということでしょうか?
1km/h=1000m/3600s=(1000/3600)m/s
と考えればよいと思います.
Re: 時速を秒速に直す公式
yama さんのレス (2007/05/12(Sat) 22:49)
>文字に付ける単位は亀甲括弧〔〕で囲んであります.
その文字が,単位まで含んだ量を表す場合と,単位を別にした数値だけを表す場合の両方の場合に対応できるように,このような表し方をするのだと思います. つまり t=10s,v=9.0m/s とすることも, ts=10s,vm/s=9.0m/s(すなわちt=10,v=9.0) とすることもできるように〔〕の中に単位を書くのだと思います.
Re: 時速を秒速に直す公式
komagatake さんのレス (2007/05/13(Sun) 06:26)
おはようございます.
私は何時も単位は[]でくくっていました.細かい規則があるかどうかは知りません.とにかく生徒が混乱しないようにということだけです.文字式が苦手というのがほとんどの生徒の現状です.mと書いてある時にメートルなのか,質量なのか区別が出来ない生徒が多いですから余分でも良いから括弧でくくれと言っています.数字が合っていれば単位が違っていても「いくらかあっているから点をくれ」といってくる生徒も必ずいます. とにかく文字式と単位はハードルなんです. 単位の変換は必ずyamaさんの書かれたように 1km/h=1000m/3600s=(1000/3600)m/s とやっています. 大きい単位から小さい単位の方に動かしていきます.小数とか分数を出来るだけ入れないようにしています.分数の分数を入れると間違いが急に増えます.kmのキロが1000ということは知っていてもmmのミリが1/1000は知らない生徒が多いです.組み合わせではなくて1つの記号だと思っているようです.高校にはいるまで知らなかったというのがほとんどです.小中ではとにかく記号として覚えるという形だったようです.[km/h]の括弧の中で計算してもかまわないというのにビックリしているという印象です.
〔〕はずっと以前からです.ただ私はどうでもいいことだと思っています.キーボードのキーの[]があるので使っています.()とは区別するようにとは言っています.とにかく数字だけでは意味がない,5[kg]と5[m],5cm]は全部意味が違うということをしつこく言わなくてはいけません.加速度の単位のs^2の部分などクラスの半分近くが間違うということが起こります.
最近は使わなくなりましたがccという単位があります.原付の50ccという言葉はほとんどの生徒が知っていました.でも50ccというのが体積だというのを知らない生徒もいます.知っていても50ccはどれくらいの大きさかと訊くとほとんどの生徒が知りませんでした.言葉として知っていても意味は知らないというのがものすごく多いです.でもそれでとにかく対応しようとしているようです.
Re: 時速を秒速に直す公式
MXK さんのレス (2007/05/13(Sun) 14:33)
> でも50ccというのが体積だというのを知らない生徒もいます.知っていても50ccはどれくらいの大きさかと訊くと > ほとんどの生徒が知りませんでした.言葉として知っていても意味は知らないというのがものすごく多いです.
その様子よく分かります.知識が紙の上に留まっていて,現実とリンクしていないのですね. モノに触れる機会が少ないのが原因なのでしょう.料理でもすれば,量についていろいろ体感できるのですが...
Re: 時速を秒速に直す公式
MXK さんのレス (2007/05/13(Sun) 15:20)
指導要領を見ると, 小学校の算数では,各学年で量,測定,単位に関する項目がきちんと系統的に扱われています. 各学年の内容を「A 数と計算」,「B 量と測定」,「C 図形」,「D 数量関係」と括っています.たとえば1年では
B 量と測定 (1)ものの長さを比較することなどの活動を通して,量とその測定についての理解の基礎となる経験を豊かにする. ア 長さを直接比べること. イ 身近にあるものの長さを単位として,その幾つ分かで長さを比べること.
となっています.
理科では対応する内容は含まれていません.
中学では,数学は数と図形に力点が移っており,量の概念は希薄になっています.理科は相変わらず,個別の内容に 集中しており,量の一般論については無関心のようです.高校でも同様です.
量,測定,単位などは中学以降では,数学と理科の隙間に置忘れられているような印象をもちました.
Re: 時速を秒速に直す公式
MXK さんのレス (2007/05/13(Sun) 18:23)
数量を文字で表すいわゆる文字式は中学2年の数学で導入されるようですが,これはあくまでも数学の文脈で行われるので,
「物理量」を文字で表すということは,正式に教えられていない可能性があります.
つまり, 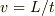 が量の関係であると,どこにも書いていないのかも知れません.
が量の関係であると,どこにも書いていないのかも知れません.
> □や△などといった記号を使った式は,小学生のころに見た覚えがありますが, > vやtなどといった文字を使った式は見たことがありません.
はそのとおりなのでしょう.
それから単位につける(意味が曖昧な)括弧については,
に詳しい報告があります.
Re: 時速を秒速に直す公式
zoro さんのレス (2007/05/14(Mon) 17:20)
●高校の物理の教科書での「次元と単位」
3社の教科書の対比をしてみました.素人めには,意外と各社の表現が違っていて驚いています.いま,後2社の教科書を手配しました.
予備的な感想ですが,細かい点を教えるより,骨格的な部分をしっかり教えてもらいたいと思います.物理量の次元,その単位,計量値などと,InternationalSystem of Units(SI)との関連も明示しながらじっくり書いて欲しいものです.
数学(計量の概念,積分,面積,体積)・化学(mol,e,電池)・英語(綴りと発音,指数の接頭辞)・世界史(文化背景と物理)などとも関連して,立体的かつ丁寧に教えてもらいたい.その為には,高校生では,定量的に理解出来ない分野は,大幅にカットするべきと思います.あと,物理数学を物理IIIとして戴きたいように思います.
●ウィキペディアにみる各国の表現
-1 日本語 --1.1 物理単位 --- http://ja.wikipedia.org/wiki/%E7%89%A9%E7%90%86%E5%8D%98%E4%BD%8D ) --1.2 自然単位系 --- http://ja.wikipedia.org/wiki/%E8%87%AA%E7%84%B6%E5%8D%98%E4%BD%8D%E7%B3%BB --1.3 幾何学単位系 --- http://ja.wikipedia.org/wiki/%E5%B9%BE%E4%BD%95%E5%AD%A6%E5%8D%98%E4%BD%8D%E7%B3%BB --1.4 次元解析 --- http://ja.wikipedia.org/wiki/%E6%AC%A1%E5%85%83%E8%A7%A3%E6%9E%90 -2 英語 --2.1 Units of measurement --- http://en.wikipedia.org/wiki/Units_of_measurement --2.2 Planck units --- http://en.wikipedia.org/wiki/Planck_units --2.3 Geometrized unit system --- http://en.wikipedia.org/wiki/Geometrized_unit_system --2.4 Dimensional analysis --- http://en.wikipedia.org/wiki/Dimensional_analysis -3ドイツ語 --3.1 Maßeinheit --- http://de.wikipedia.org/wiki/Ma%C3%9Feinheit --3.2 Planck-Einheiten --- http://de.wikipedia.org/wiki/Planck-Einheiten --3.3 n.k. --3.4 Dimensionsanalyse --- http://de.wikipedia.org/wiki/Dimensionsanalyse -4 仏語 --4.1 Unité de mesure --- http://fr.wikipedia.org/wiki/Unit%C3%A9_de_mesure --4.2 Unités de Planck --- http://fr.wikipedia.org/wiki/Unit%C3%A9s_de_Planck --4.3 n.k. --4.4 Analyse dimensionnelle --- http://fr.wikipedia.org/wiki/Analyse_dimensionnelle
● 単位の変換の実例:ウィキペディア英語版
このうち,「2.4 Dimensional analysis」に単位の変換の実例があったので,式の部分だけ引用します.詳しくは,直接のリンク先をご覧下さい.
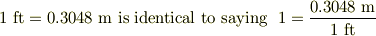
#味噌は,同じ「長さ」という次元をもつ計量を,異なる計量単位で表現した場合.
#左の等式は,異なる計量単位相互の換算をしめす. #右の等式は,同一の次元間の比だから,左辺の「1」はディメンションレス.
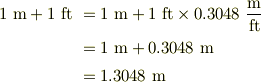
当たり前のことですが,初学者は安心して,換算できるように感じました.
Re: 時速を秒速に直す公式
toorisugari no Hiro さんのレス (2007/05/15(Tue) 16:35)
> * --1.1 物理単位 > --- http://ja.wikipedia.org/wiki/%E7%89%A9%E7%90%86%E5%8D%98%E4%BD%8D )
ここに書かれている密度の定義ですけど,おかしくないですか?
>>「密度は単位体積あたりの質量である」という表現は「体積の『単位』によって割られた質量」という意味ではない.この「単位体積」という表現は「数値1と現在使用している体積の単位によって作られる『体積』」を示す.たとえば体積の単位として 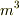 を用いている場合,「単位体積」は
を用いている場合,「単位体積」は ![1[\boldmath{m}^3]](http://hooktail.maxwell.jp/bbslog/5ff4cbd641a6b0ee706a165fac85b068.png) である.ある均質な物質の質量を
である.ある均質な物質の質量を  ,体積を
,体積を  ,現在使用している単位系での単位体積を
,現在使用している単位系での単位体積を 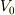 とすると,この物質の密度
とすると,この物質の密度  は以下のように表される.
>>
は以下のように表される.
>>
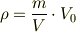
Re: 時速を秒速に直す公式
zoro さんのレス (2007/05/15(Tue) 18:14)
>> --- http://ja.wikipedia.org/wiki/%E7%89%A9%E7%90%86%E5%8D%98%E4%BD%8D ) > >ここに書かれている密度の定義ですけど,おかしくないですか?
あっ,気が付きませんでした.今回,教科書見るほどに混乱が増し,参考に各国の解説をそこそこに反映しているウィキペディアならと思い拝見して,こちらの説明もバラバラで,驚いています.
その上,この密度の説明は理解出来ません.何か説明に飛躍がある;中間式の欠落がある;ような気がします.さらに,密度の事例は,少なくとも英語版にも対応の部分が在りません.
ここまで来ると,SI単位系での記述を勉強するしか無いのかも知れません.何たることか.
しかし,高校の教科書というのは検定されていて,国家の威信と権威を背負った存在の筈だが,こんな時に頼りになれないとは!!!!!!!!,何たる事か.
Re: 時速を秒速に直す公式
MXK さんのレス (2007/05/15(Tue) 18:48)
たしかに,「密度は単位体積あたりの質量である」という表現が変だという指摘は正しいのですが, その後の説明がよく分からないですね. 分母が無次元のときは,「一人あたりの収入」とかはそれなりに意味があるのですが, 次元つきの場合は,「単位XXあたりの」という表現は正確ではありませんね.
単位に依存しない言い方が欲しいのですが,なかなかいい表現が思いつきません. 「質量-体積比」,「体積で規格化した質量」とかでしょうか.
Re: 時速を秒速に直す公式
toorisugari no Hiro さんのレス (2007/05/15(Tue) 19:17)
>> 「体積の『単位』によって割られた質量」という意味ではない.
ふむふむ.とおもったんですが....
>> この物質の密度rhoは以下のように表される. >> rho = frac{m}{V}cdot V_{0}
これは密度でなく単位体積 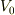 の「質量」になってしまいます.(字義どおり単位体積あたりの質量.........だが,単位質量が全面に出てるのが怪しい.)
の「質量」になってしまいます.(字義どおり単位体積あたりの質量.........だが,単位質量が全面に出てるのが怪しい.)
密度は 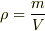 ですよね.ただ,これを表す言葉が...
ですよね.ただ,これを表す言葉が...
> たしかに,「密度は単位体積あたりの質量である」という表現が変だという指摘は正しいのですが,
でも,これだと,「単位時間あたりに進んだ距離」は「速さ」でなく「距離」の次元を持つ量になってしまいますよね.
ここら辺,しっかりとした基準がないと,微分さえ伝えられなくなってしまう.
Re: 時速を秒速に直す公式
zoro さんのレス (2007/05/15(Tue) 19:22)
>単位に依存しない言い方が欲しいのですが,なかなかいい表現が思いつきません.
なるほど,「単位に依存しない言い方」こういう概念で捉えるのか.単位は言わす,次元だけを言えばどうでしょうか.
#ある物質が均一と見なせるとき,適当な表面Sに囲まれた部分の質量Msを,その体積Vsで割ったものを,その物質の密度ρsと定義する.
#ρs := Ms ÷ Vs
あー,判らない!!!!!!
Re: 時速を秒速に直す公式
zoro さんのレス (2007/05/15(Tue) 19:29)
>「単位時間あたりに進んだ距離」は「速さ」でなく「距離」の次元を持つ量になってしまいますよね.
考察する運動物体が,微小時間幅Δtの間に,微小距離ΔL進んだとき,その速度Vを;
V := ΔL ÷ Δt
どうも,割り算が入ると難しくなるのはどうしてだろうか.
「…あたりの…」
山旅人 さんのレス (2007/05/15(Tue) 22:15)
みなさん,こんにちは.
>「密度は単位体積あたりの質量である」 確かに,『質量である』 と読んでしまうと違和感を感じなくもありませんが,『単位体積あたりの質量』で,それは 『m/V のこと』(単位 kg/m 3 ) とすることに私は特に抵抗はありません.そのように受け入れないと,言葉によって 「密度」 が定義できなくなってしまうと思います.
Re: 「…あたりの…」
MXK さんのレス (2007/05/16(Wed) 00:47)
各量を,数値(ダッシュつき)と単位(添字0)に分けて書くことにします.
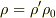 ,
, 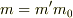 ,
, 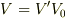
物理量を単なる数だとする立場では
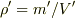 に
に 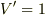 を代入すれば,
を代入すれば,
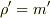 となって,文字通り,「密度」=「単位体積に対する質量」に
なります.
となって,文字通り,「密度」=「単位体積に対する質量」に
なります.
物理量を次元つきの量と思う立場では,
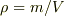 に
に 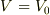 を代入すると,
を代入すると,
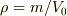 となるだけで,これ以上なかなか進みません.
となるだけで,これ以上なかなか進みません.
「密度は単位体積に対する質量」という表現は前者の立場に密着しています. 後者の立場に相応しい表現があればうれしいのですが.
単位系の 煩雑さ
かめ吉 さんのレス (2007/05/16(Wed) 13:14)
はじめましてこれは質問ではありません. 最近EMANの物理の作者の本を購入して趣味で物理をよみふけっている 五十一の親父です.世界統一の単位系無理かな・・・・ それぞれの国の文化的背景歴史もあるし・・・・ マクスウェルの方程式でRot,DIVetc色々な数学的概念がでてきて苦労しております.唯一感覚的にわかるのはdivB=0 モノポールは今のところ 存在しないらしい.みなさんの力をお借りして電磁気学をも少し深く勉強したいと思っているところです.突然失礼いたしました. 日本も捨てたものではないですね.
Re:時速を秒速に直す公式
zoro さんのレス (2007/05/17(Thu) 18:23)
netwireさん,
紆余曲折しましたが,英語版ウィキペディアの次元解析;
-2.4 Dimensional analysis -- http://en.wikipedia.org/wiki/Dimensional_analysis
のIntroduction中頃にある文が参考になるとおもいましたので,下記に引用します;
>The value of a dimensional physical quantity is written as the product of a unit within the dimension and a dimensionless numerical factor. (次元のある物理量とは,次元を示している単位と次元を持たない数値因子との積,として書かれるものだ.)
これをヒントに以下の様な考察をしましたので,ご報告します.
〜〜〜〜
以下では具体的に,ある物体の長さ, 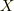 ,について表現する事を検討します.
,について表現する事を検討します.

ここで単位「u」は長さの次元をもつ単位で,例えば「尺」とか「インチ」,「mm」とか「km」,そして勿論「m」でもよい.
また, 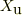 は,単位uに対応する数値因子を意味する.従って;
は,単位uに対応する数値因子を意味する.従って;

すると,少し奇妙な表現;

となります.ところが良く似た事例があります;
*ヴェクタ解析の始めに,およそヴェクタは基底に依らず等しい事を示す為に,次の変形をしますね;
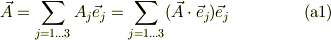
これからの類推でいえば,科学的な計量空間は,それぞれの次元の物理量ごとに,「計量単位」を基底ヴェクタとした1次元空間でのスケイラと考えられそうです.
#ここら辺の考え方に付いては,数学の強い方の解説が待たれる所です.
次に,二つの単位での表現を考えます.一つ目は,「u := 尺 ="Shaku"」,二つ目は,お約束の「v := m」です.当然のこと式(1)に従い,

この特別の場合として,単位の長さ「尺」,言うならば "length of a single 'Shaku'-unit ",を考えれば,
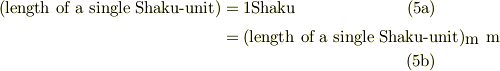
こここで式(5b)の係数は,「尺」を「m」に換算する因子,"conversion factor"(セクション3.1を参照)に他ならない.
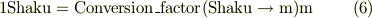
この式を式(4)に適応するする為に,単位名を書き換えると
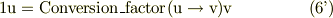
だから,式(4a)に代入して,
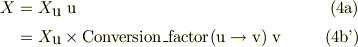
これと式(4b)とを比較して;
ある物理量を単位"u"での表示を,単位"v"での表示に書き換えるには;
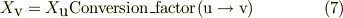
と変換すればよい.
なお,同様にして「km」→「m」などの換算も出来るのですが,書くのをサボりました.じっさいの計算で確かめてください.
また,以上の事があるので,通常の物理計算にでてくる変数は,このような意味で単位を自然な形で含んでいるので,理論式を立てる時も,気楽に使い,数値として算出する時に,今回のバックグランドを利用して,やり易い方法で計算されるように期待します.
〜〜〜〜
以上,大凡の流れを追ってみました.いつも当たり前のように式をハンドリングしていますが,適当にしていました.ヴェクタ解析の論議で,単位と係数の関係をこれから検討する上で,とても参考になります.
良い質問を戴き,感謝致します.
Re:時速を秒速に直す公式
zoro さんのレス (2007/05/18(Fri) 21:55)
肝心の公式を作っていなかったのでトライします.
要は,物理量としての早さ,  を考えます.
を考えます.
単位系を次の2つに取るとすれば

単位の換算は;
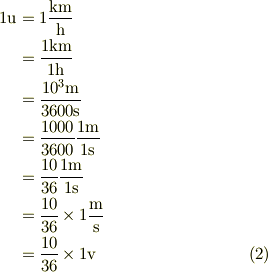
物理量は単位換算に対して普遍だから,
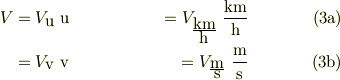
従って,数値因子に着目して整理すると,式(2)を適用すれば
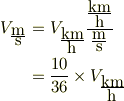
と尤もらしくはなりますが....
結局,直感的に変形するのと同じですね.確かに公式を作る必要は無いようです.ただ,今度は自信をもって,根拠はこれだと言える事でしょうか.
むしろ,ヴェクタ解析で,異なる次元のヴェクタ間の内積や外積でも,わざわざ単位で割って,また掛けてという,リダンダントな作業は要らなくなったのが嬉しいように思います.