波動関数の量子数の決定
波動関数の量子数の決定
カイ さんの書込 (2007/05/10(Thu) 16:06)
こんにちは.量子力学を勉強しはじめたばかりの者です. 量子数についての疑問なのですが, 波動関数は,量子数という任意な部分を残しているわけですが,実際の実験などの際,どのように量子数は決定されるのでしょうか?
例えば,正方形の箱に閉じ込められた3次元の自由電子で,nが(1,1,2)の場合を観測したいなあ,と思ったらどのような操作をしてやればよいのですか? 古典力学の場合,初期条件として,ある時刻の位置と速度を与えてやれば状態は決まりますが, ある状態の波動関数を決めてやろうとしても,不確定性原理から位置と運動量を同時に決めることは不可能と知りました. 光を当ててやるなどして,(1,1,2)の固有エネルギーを作ってやればよいのかとも考えましたが (1,1,2)の場合は3重に縮退しているので,まだ,3種類の状態の自由度が残るわけですよね? その3パターンの状態のどれを取るかも,確率で決まるのですか?
Re: 波動関数の量子数の決定
zoro さんのレス (2007/05/10(Thu) 19:39)
カイさん,初めまして.
私は,量子力学を再勉強し始めている者です.昔,読めなかった本を少しかじり始めているので,逆に,簡単な所が未だ朧げです.
でも,すこし解る所をコメントします.詳しいことは,別の方々から教えてもらって下さい.
さて >正方形の箱に閉じ込められた3次元の自由電子
と考えると,ある意味間違いです.「閉じ込められた」ら,すでに自由電子ではありません.確かに箱内部にいる限り力を受けませんが,箱に接近すると急激に大きな力を受けます.
その意味では,近くのスレッドで「1次元調和振動子」の問題で,零点エネルギの論議がありますが,今回の場合も,x,y,zの振動に対応して,3つの量子数が出て来るのでしょうが,「各量子数>=1」ですよね.この最低順位でも持つエネルギが零点エネルギであり,系が有限領域に限定されている事に対応しますし,エネルギ順位が離散的になっているのも同根だと思います.
さて,純粋に箱形ポテンシャルだけでしたら,ご推察の様に,エネルギ順位は縮退して,何処にいるかは確率的におなじだろうと思います.
ところが,微小な磁場を印加するなどの外乱を付けたら,その縮退は解けると思います.具体的にどのような磁場を与えると巧く順位が分裂できるのか,分離しても連続的な分布になるかなどの問題はあるとおもいますが.
Re: 波動関数の量子数の決定
クロメル さんのレス (2007/05/10(Thu) 23:00)
(ここの議論はあとでyamaさんがおっしゃってますが,正しくないようです.)
はじめまして,カイさん.
カイさんが例に挙げた,量子数nは運動量pを測っていることと同じですね.
( 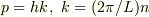 )
おっしゃる通り位置と運動量は同時に測定できません.
しかし,この場合にかぎっては,量子数を知りたいのなら運動量だけを測ればいいような気がします.なぜなら,x,y,z方向の運動量は,同時固有状態ですので,
x方向の運動量を測っても(運動量は振動数の弱い光をあてて測るのでしたっけ?)位置は分りませんが,運動状態は壊されません.よって,y,z方向も同様に測ってやればいいのだと思います.ただし,実際に実験できるかどうかは分りません.理論上はの話です.更に,この場合,測るといっても運動量の測定誤差によって,量子数はある幅の不確定性を残すと思いますが….
一般論になると,電子のうまい物理変数(オブザーバブル)を測定して量子状態を決定できるか,私にもよくわかりません.
)
おっしゃる通り位置と運動量は同時に測定できません.
しかし,この場合にかぎっては,量子数を知りたいのなら運動量だけを測ればいいような気がします.なぜなら,x,y,z方向の運動量は,同時固有状態ですので,
x方向の運動量を測っても(運動量は振動数の弱い光をあてて測るのでしたっけ?)位置は分りませんが,運動状態は壊されません.よって,y,z方向も同様に測ってやればいいのだと思います.ただし,実際に実験できるかどうかは分りません.理論上はの話です.更に,この場合,測るといっても運動量の測定誤差によって,量子数はある幅の不確定性を残すと思いますが….
一般論になると,電子のうまい物理変数(オブザーバブル)を測定して量子状態を決定できるか,私にもよくわかりません.
こうゆう話は,確信しているわけではありませんが,ファインマン物理学(?)「量子力学」に載っていそうだなと思いました. すくなくとも,こうゆう疑問を持つ方には,お勧めの本だと思います. (もっていたらごめんなさい) お力になれず,すみません.
Re: 波動関数の量子数の決定
zoro さんのレス (2007/05/11(Fri) 00:25)
>量子数を知りたいのなら運動量だけを測ればいいような気がします.
昔話ですが,このように考えるときに,「力学的に無限大のポテンシャルに穴があけられるか?」という大論争をした事があります.当時の結論では,かりに穴が開けても,その近傍で強いポテンシャル勾配ができて,低い順位状態に摂動が強すぎて意味が無いといった結論になりました.
そこで,カイさんのご提案のような分光学的な測定を考えました.その時には,原子になぞらえて,円筒形の容器を考えて,容器の軸に磁場をかけたらどうだろうかと考えました.円筒座標形でいえば,z軸方向に磁場をかけていくとどうだろうかとおもいました.
近年では,人工原子などが出来る時代ですから,実験的に出来ませんかね?
Re: 波動関数の量子数の決定
カイ さんのレス (2007/05/11(Fri) 01:19)
zoroさん,クロメルさんありがとうございます.
申し訳ないのですが,僕はまだ量子力学を始めたばかりなので お二人の仰っていることがあまり理解できません.
運動量を測ることが,主量子数を測るということと同等とのことですが それはエネルギーを測ってやることと似ていますね. 運動量は縮退しないのでしょうか? お二人も,測定の案を考えて下さっていますが,確立されているものではないのでしょうか. というより,「波動関数がどの主量子数の状態を取るのか?」ということ自体,考える必要のないことなのでしょうか. 教科書を見ても,波動関数とエネルギーを求めたところで終わっていて 電子が現実にはどういう振る舞いをするのかが書いてないんです. 弦の振動も,同様にnの入った形での解になってしまいますが,初期条件を与えてやる 例えば,ギターならどの位置からどのくらいの強さで弾くかによって,現実に起こる振動が記述できますよね. 波動関数の場合はどうなのか,箱に電子を入れてやったとき,そこにはn=1が起こるのかn=2なのかn=3なのかそれがわからないんです.
答えてくださったのに質問ばかりで長くなってしまってスミマセン.ファインマン読んでみます.
Re: 波動関数の量子数の決定
zoro さんのレス (2007/05/11(Fri) 07:25)
>電子が現実にはどういう振る舞いをするのかが書いてないんです.
どのような解説をご覧になってるかにも依りますが...,この場合,ギターの弦と同じで,定常的な波,言い換えれば,左右の進行が等しく起こっているとイメージしたら良いのでは.
ただ,重要なのは,ポテンシャル障壁が巨大なために,その外部に波動関数がしみ出せない事ですね.
現実に考えるのは難しそうですが,ポテンシャル障壁が無い時に外部から,ある程度のエネルギがそろった,逆に言えば,位置がブロードな電子群を注入後,ポテンシャル障壁を作れば,トラップ出来るとおもいます.
>運動量は縮退しないのでしょうか?
もちろん,「量子数, 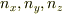 」と運動量には,一対一で対応関係がありますので,縮退があるとは言えませんね.あえていえば,先に述べた定在波としての左右方向成分が等しく重ね合わされていますね.
」と運動量には,一対一で対応関係がありますので,縮退があるとは言えませんね.あえていえば,先に述べた定在波としての左右方向成分が等しく重ね合わされていますね.
>運動量を測ることが,主量子数を測るということと同等とのことですが >それはエネルギーを測ってやることと似ていますね.
運動量(ベクトル)の測定問題は,エネルギ測定(スカラ)とは意味合いが違うとおもいます.運動量測定にはスリット系が入り込むので,簡単ではないと思います.
Re: 波動関数の量子数の決定
yama さんのレス (2007/05/11(Fri) 08:45)
この場合,運動量は確定値をもたないので,運動量を測定して量子数を決めることはできないと思います. そもそも運動量の固有関数は全空間に広がっていなければならないので,有限の領域に限られたものは固有関数にはなりません. 不確定性原理からも,有限の領域に閉じ込められた粒子の運動量が確定しないことは明らかです.
Re: 波動関数の量子数の決定
カイ さんのレス (2007/05/11(Fri) 12:44)
zoroさん,yamaさんご回答ありがとうございます.
運動量を観測してもダメですか. なんか,観測中心の話に移っているので,僕の言いたいことがうまく伝わっているか不安なのですが,(うまく日本語にできなくてすみません.)
一番知りたいのは,例えば,僕が電子を箱に入れたあと,箱の中を観測すると どのような確率密度が観測されるのだろう?ということなんです.箱じゃなくても構いません.どんなポテンシャルでもいいのですが. シュレディンガー方程式を解くと,確率密度を与えるψnは求められますが,箱の中を観測したとき,ψ1が観測されるのかψ2が観測されるのかψ3が観測されるのか nはどのように決まるのか,それが一番疑問なんです. それで一番最初の >正方形の箱に閉じ込められた3次元の自由電子で,nが(1,1,2)の場合を観測し>たいなあ,と思ったらどのような操作をしてやればよいのですか? >光を当ててやるなどして,(1,1,2)の固有エネルギーを作ってやればよいのかと>も考えましたが >(1,1,2)の場合は3重に縮退しているので,まだ,3種類の状態の自由度が残る>わけですよね? です.
Re: 波動関数の量子数の決定
zoro さんのレス (2007/05/11(Fri) 13:10)
少し見方を変えてみます.
世界で一番簡単な系は「水素原子=陽子+電子」と思います.この場合,色々な細かな相互作用を含め,さらに相対論的な計算すらきちっと計算されていると思います.
では,そのそれぞれの波動関数の量子数を直接的に実験でだせるかといえば,「否」だと思います.直接的に求まる物理量(観測可能な量)は,基底状態での質量,電気的双極子モーメント,磁気的双極子モーメント,電気的四重極子モーメントなどではないでしょうか(モッと在るかも知れませんが).
他方,励起順位間のエネルギ放出;電磁波,電子;などは,順位間のエネルギ差に対応します.エネルギ放出に伴う遷移確率(準位の寿命)は,関与する電磁場の種類(いわゆる多重極モーメント)を考察する準位の波動関数とで挟んで積分した多重極モーメントの対角成分によって与えられます.
このように,量子数を直接的に検証する事はとても希有なことだと思います.
あ,物性物理における事例はどうなんでしょうか?
Re: 波動関数の量子数の決定
nomercy さんのレス (2007/05/11(Fri) 22:29)
カイさんのような疑問を昔量子力学を学びたての頃に感じたことがあります.
カイさんの言う通り,Newton方程式では初期条件を与えないと解が一意に決まりません. これは量子論でも同様です. Schrödinger方程式も所詮は微分方程式なので初期条件が必要です.
Schrödinger方程式を解く,とは
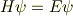
という固有値問題を解くことだ,と考えていると思います. これは古典力学で言えば,振動の問題において基準振動を求めるということです. 振動数(エネルギー)とその振動の状態(波動関数),およびその時間発展の仕方はこの固有値問題だけから分かります.
では量子論の場合に初期条件とは何か? これは古典論がそうであったように,状況によって様々です.
一つの例として統計力学を考えてみます. 箱の中に沢山の粒子が詰め込まれており,それが温度Tの平衡状態になっているとします. これがいわば初期条件を与えたようなものです. この場合には比熱や粒子数密度分布などの巨視的な物理量を統計力学の知識を使って決定することが出来ます.
Re: 波動関数の量子数の決定
カイ さんのレス (2007/05/12(Sat) 01:35)
nomercyさん,同じ疑問を持っている方がいらして嬉しいです. 初期条件を与えてやれば,主量子数も決まるのでしょうか. 古典力学と同じように,フーリエ積分で重ね合わせる感じですかね? 一番最初に例に挙げた,三次元の箱の中の一電子に初期条件を与えると具体的にどんな感じになるのか,教えていただけませんか? 温度Tの平衡状態を与えてやるということは,一定のエネルギーを与えてやるのと同じだと思うのですが,それが縮退している場合の量子数(112,121,211が縮退しているとしたら,この3つのうちのどれが観測されるか)はやはり確率で決まるのでしょうか?
Re: 波動関数の量子数の決定
nomercy さんのレス (2007/05/12(Sat) 02:10)
>初期条件を与えてやれば,主量子数も決まるのでしょうか.
初期条件次第では主量子数も一つに決まると思います.
例えば系が初期に第一励起状態にあったとします.
(実際にそのような状態を実現することが出来るかどうかという点は置いておきますが.)
第一励起状態は三つありますが,これらの振幅を 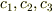 と書くことにすると時刻tにおける波動関数は
と書くことにすると時刻tにおける波動関数は
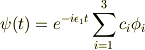
となります.
どの時刻においても状態 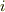 を見出す確率は
を見出す確率は 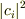 です.
です.
これを一般的に考えると,まさに
>古典力学と同じように,フーリエ積分で重ね合わせる感じですかね?
となります.
>温度Tの平衡状態を与えてやるということは,一定のエネルギーを与えてやるのと同じだと思うのですが,それが縮退している場合の量子数(112,121,211が縮退しているとしたら,この3つのうちのどれが観測されるか)はやはり確率で決まるのでしょうか?
そうなります. 平衡状態においてはエネルギーが同じこれらの三つの状態は同じ確率,つまり確率1/3で出現します. ただ,温度Tにおいて測定すると例えば(112)の波動関数が確率1/3で観測される,というわけではなく,正確に言えば比熱などの物理量に対してこれらの三つの状態が同じ割合で寄与を与える,ということになります. だんだん統計力学の話になってきますのでこの温度Tの平衡状態という話はこの辺で止めておきます.
Re: 波動関数の量子数の決定
zoro さんのレス (2007/05/12(Sat) 02:35)
nomercyさん,
>カイさんの言う通り,Newton方程式では初期条件を与えないと解が一意に決まりません. >これは量子論でも同様です.
少し気になる所があります.量子論の場合,初期条件というよりは境界条件が本質的だと思います.
勿論,ウェイブ・パケットのような取り扱いをするのなら,状況は異なるかも知れませんが,仮にそこから出発しても,時間とともにパケットは崩れ,通常の定在波のモードに移行するように思います.
これは,ギターの弦で,端の部分に部分的な衝撃を与えても,最終的には振幅は少ないけれど,定在波モードが残るのと同じだろうとおもいます.(弦でのエネルギ損失も重要かも?)
古典的でも,量子力学的でも,振動が有限領域に閉じ込められていると似た振る舞いをするのではありませんか.
Re: 波動関数の量子数の決定
nomercy さんのレス (2007/05/12(Sat) 03:27)
zoroさん
古典論でも量子論でも境界条件を決めて初めて基準振動・固有状態,およびその振動数・エネルギーが決まります. そのような意味では境界条件は重要な要素です. 境界条件・初期条件の役割は古典論・量子論で同じであると私は捉えています.
ところで多くの場合,境界条件の取り方はどうでも良いことが多いです. それは考えている領域が非常に広い場合です. このときにはどのような境界条件を選ぼうとも,境界の影響は反映されません. もちろん,あからさまに有限の領域を考えるならば境界条件の違い(固定端・周期境界んなど)が効いてきます. このような有限系の物理も近年の実験技術の発展にともない盛んに研究されるようになって来ました.
勿論,ウェイブ・パケットのような取り扱いをするのなら,状況は異なるかも知れませんが,仮にそこから出発しても,時間とともにパケットは崩れ,通常の定在波のモードに移行するように思います.
これは,ギターの弦で,端の部分に部分的な衝撃を与えても,最終的には振幅は少ないけれど,定在波モードが残るのと同じだろうとおもいます.(弦でのエネルギ損失も重要かも?)
この点に関してコメントします. 主旨は 「初期状態として波束を用意しても,十分時間がたてば初期状態に依存しないモード分布に至る」 ということでしょうか?
実はSchroedinger方程式を考えているだけではこれは実現しません.
時刻  における波束が次のように構成されているとします.
における波束が次のように構成されているとします.
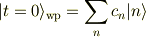
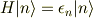
すると時刻 
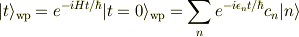
となりますが,時刻tにおいて 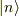 が見出される確率は
が見出される確率は
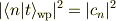
となり,初期のモード分布がそのまま反映されます. 初期条件に依存して終状態の様子が決まってしまうことになります.
しかし実際にはこれとは逆に 「初期状態として波束を用意しても,十分時間がたてば初期状態に依存しないモード分布に至る」 というのが現実的には起こりえます. 実際には外界との何かしらの相互作用があるので,これを通じて 系は一定のモード分布に至ります. これがつまり平衡状態であって 統計力学の考えに他なりません.
結局,何かしら初期条件を与えなければ系の振る舞いは一意には決まりません.
Re: 波動関数の量子数の決定
nomercy さんのレス (2007/05/12(Sat) 03:36)
先ほどから統計力学を舞台にしてしまっていたので, 量子力学において一番最初に出会うであろう,一次元のポテンシャルの透過について述べてみます.
この問題では透過率,反射率という物理量を求めることが目的です. これは入射流束と透過流束の比,および入射流速と反射流速の比です. これを求めるために
左から平面波 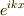 を入射させ,
反射波
を入射させ,
反射波 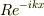 が生じ
透過波
が生じ
透過波 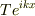 が生じる
が生じる
という舞台設定をしますが,これが初期条件 (粒子は波数kのものが左側だけから飛んでくる) を与えたことになります.
これの下で実際の計算をするわけですね.
勿論計算の途中ではポテンシャル境界における境界条件を適切に取り入れなければなりません.
Re: 波動関数の量子数の決定
カイ さんのレス (2007/05/12(Sat) 11:33)
>nomercyさん まさに僕が知りたかった答えです!ちょっとずつわかってきました. ありがとうございます. 古典振動と同じなのですね.しかし,まだ幾つか質問があります.
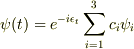 の
の 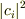 が存在の確率になるというのは初めて聞きました.
ψの2乗が存在確率になるのは知っていましたが.
古典振動の知識で推測すると
おそらく,シュレディンガー方程式→変数分離→時間に依存しない方程式→境界条件→固有エネルギーとそれに対応する波動関数→初期条件→重ね合わせ→最終的な波動関数
みたいな流れになると思うのですが,僕の教科書だと(おそらく自分の勉強不足が原因だと思いますが)時間に依存しない方程式を解いて,基準振動を求めたところで終わっています.どの辺で重ね合わせの話が出てくるのでしょうか?
(これから,調和振動子,水素原子と進んでいくところです)
それと,
>平衡状態においてはエネルギーが同じこれらの三つの状態は同じ確率,つまり確>率1/3で出現します.
の1/3というのは,
が存在の確率になるというのは初めて聞きました.
ψの2乗が存在確率になるのは知っていましたが.
古典振動の知識で推測すると
おそらく,シュレディンガー方程式→変数分離→時間に依存しない方程式→境界条件→固有エネルギーとそれに対応する波動関数→初期条件→重ね合わせ→最終的な波動関数
みたいな流れになると思うのですが,僕の教科書だと(おそらく自分の勉強不足が原因だと思いますが)時間に依存しない方程式を解いて,基準振動を求めたところで終わっています.どの辺で重ね合わせの話が出てくるのでしょうか?
(これから,調和振動子,水素原子と進んでいくところです)
それと,
>平衡状態においてはエネルギーが同じこれらの三つの状態は同じ確率,つまり確>率1/3で出現します.
の1/3というのは, 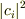 が1/3になるということでよろしいですか?
(おそらく,どの状態も対称であることから1/3が出てきたと思いますが.)
が1/3になるということでよろしいですか?
(おそらく,どの状態も対称であることから1/3が出てきたと思いますが.)
統計力学はまだ殆ど無知なのですが,あわせて勉強します.
Re: 波動関数の量子数の決定
zoro さんのレス (2007/05/12(Sat) 16:15)
nomercyさん,
>ところで多くの場合,境界条件の取り方はどうでも良いことが多いです. >それは考えている領域が非常に広い場合です. >このときにはどのような境界条件を選ぼうとも,境界の影響は反映されません.
これは,具体的な話とする,無限の空間を運動する自由粒子を想定してるのでしょうか.前後の文脈が理解出来ませんでした.
>もちろん,あからさまに有限の領域を考えるならば境界条件の違い(固定端・周期境界んなど)が効いてきます. >このような有限系の物理も近年の実験技術の発展にともない盛んに研究されるようになって来ました.
今問題になっているのは,まさに「あからさまに有限の領域」を対象としていると理解していました.
> 実はSchroedinger方程式を考えているだけではこれは実現しません. 時刻t=0における波束が次のように構成されているとします.

すると時刻における波束は
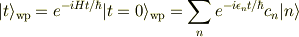
となりますが,時刻tにおいて|nrangleが見出される確率は
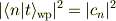
となり,初期のモード分布がそのまま反映されます. 初期条件に依存して終状態の様子が決まってしまうことになります. <
私は量子力学でポテンシャル問題に初めて勉強した時に平面波近似に とても驚いて「パケット表示」で色々悩みました.上のご解説は,フーリエ展開で言えば,ある波形のパワー・スペクトルが時間について不変だと言うご主張とおもいます.
しかし,いま論議している「パケット」波の形状を意味している訳です.上の表現は,エネルギ固有値とその固有関数で波動関数を展開している訳です.よほどエネルギ固有値が単純な場合を除き,時間に伴って位相因子 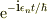 が複雑に変化した結果,長い時間の後には,定常状態に陥るのだと思っていました.
が複雑に変化した結果,長い時間の後には,定常状態に陥るのだと思っていました.
また,境界条件は,固有関数を定めた時に組み込まれているのですね.
> しかし実際にはこれとは逆に 「初期状態として波束を用意しても,十分時間がたてば初期状態に依存しないモード分布に至る」 というのが現実的には起こりえます. 実際には外界との何かしらの相互作用があるので,これを通じて 系は一定のモード分布に至ります. これがつまり平衡状態であって 統計力学の考えに他なりません. <
やはり「純粋に量子力学の問題」を「統計力学」と直結して解釈するのには釈然としません.統計力学は得意でなかったので,もう少し解説を下されば幸いです.
>結局,何かしら初期条件を与えなければ系の振る舞いは一意には決まりません.
もう少しブレイクをお願い出来ますか?
Re: 波動関数の量子数の決定
nomercy さんのレス (2007/05/12(Sat) 17:12)
カイさんの言うとおり,波動関数が
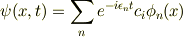
と与えられたとき,時刻t,位置xに粒子を見出す確率は
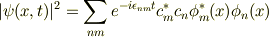
となります.
また 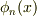 という状態が見出される確率は
という状態が見出される確率は
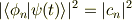
です.
これら二つは言っている意味が異なります.
後者について例を述べると,
「時刻  においてエネルギーが
においてエネルギーが 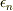 と測定される確率は,
と測定される確率は, 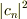 となる」
という感じです.
となる」
という感じです.
>古典振動の知識で推測すると おそらく,シュレディンガー方程式→変数分離→時間に依存しない方程式→境界条件→固有エネルギーとそれに対応する波動関数→初期条件→重ね合わせ→最終的な波動関数
これはまさしくその通りです. すると当然
>時間に依存しない方程式を解いて,基準振動を求めたところで終わっています.どの辺で重ね合わせの話が出てくるのでしょうか?
という疑問を感じると思います.
実際は固有値と固有関数を求めるところまでで十分なのです.
これが分かればその系は理解できた,と言えます.
初期条件を反映させるのは重ね合わせるだけなので.
逆に初期条件としては様々なものが考えられるので,普遍的なものである固有値と固有関数を求めるだけという最小限のことをしているだけです.
つまり,物理量を計算するには固有値と固有関数だけ分かっていれば良いのです.
例として(また統計力学になってしまいますが)自由粒子系の適当な物理量 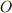 の統計平均を考えてみます.それは
の統計平均を考えてみます.それは
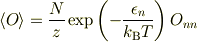
となります.固有関数が分かれば 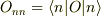 が計算できるので,固有値と固有関数が分かれば統計平均が計算できます.
が計算できるので,固有値と固有関数が分かれば統計平均が計算できます.
>>平衡状態においてはエネルギーが同じこれらの三つの状態は同じ確率,つまり確>率1/3で出現します.
1/3というのは間違いでした. 三つの状態がそれぞれ同じ確率で現れるというのは正しいですが. というのは熱平衡状態では第一励起状態だけ含んでいる,ということは起こらずに全てのエネルギーの状態がある割合で混ざっています. これに伴って
> |11c6c7c5315d7d87733843b62e68199a| が1/3
の間違いを直すと"大体" 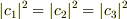 となります.
"大体"と言いましたが,この辺が繊細なところで,物理量の統計平均値に対しては,これら三つの状態がそれぞれ同じだけの寄与をする,というのがおそらく一番正しい表現になります.
この辺の微妙なところは統計力学を一通り学び終えてから考えてみた方が良いでしょう.今の段階ではあまり拘らない方が良いです.
となります.
"大体"と言いましたが,この辺が繊細なところで,物理量の統計平均値に対しては,これら三つの状態がそれぞれ同じだけの寄与をする,というのがおそらく一番正しい表現になります.
この辺の微妙なところは統計力学を一通り学び終えてから考えてみた方が良いでしょう.今の段階ではあまり拘らない方が良いです.
Re: 波動関数の量子数の決定
nomercy さんのレス (2007/05/12(Sat) 17:56)
zoroさん
>ところで多くの場合
これは今考えている"箱"の系以外の話ですね. 固体中の電子,とか自由空間での素粒子とか. 余談ということで.
>しかし,いま論議している「パケット」波の形状を意味している訳です.
実空間での波動関数の形ということですね. 確かにこれは十分時間が経った後に適当な定在波に収束すると思います. (実際に確認してみると面白いかもしれないと思った) さて,最終的な波動関数の形ですがこれが初期状態に依存する気がします. もちろん実際に確認してみないといけませんが. もしそうだとすると この観点では,初期条件に依存して系の振る舞いが異なる,ということになります.
これをモード分布の面から眺めると,先程言ったようにモード分布 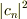 は時間に依存しないということから,モード分布は初期条件により異なる,ということになります.
は時間に依存しないということから,モード分布は初期条件により異なる,ということになります.
>やはり「純粋に量子力学の問題」を「統計力学」と直結して解釈するのには釈然としません.
ごもっともです. そこで一つの例をNo.15791にて示してみました. ちなみに何度も統計力学を論じていたのは,これが初期状態に依存しない物理量を論じているからでした. また,
>「初期状態として波束を用意しても,十分時間がたてば初期状態に依存しないモード分布に至る」
というのはいわゆる緩和現象というもので, 系に何かの偏りを起こしておいても,最終的には熱平衡状態に移行するというものです. 緩和が起こるにはどこかにエネルギーの逃げ道が必要ですが,これが外界との相互作用であったりします. これも余談ですね.
Re: 波動関数の量子数の決定
カイ さんのレス (2007/05/12(Sat) 20:37)
nomercyさん,ありがとうございます. よく理解できました. 時間を含まない波動関数がさまざまな電子状態の共存状態であるだけでなく さらに時間変化しながら,いろんな波動関数が混ざり合っているのですね.エネルギーも混ざり合ってるとなるとかなり複雑ですね^^; しかし,意外と古典的な振動と計算の流れは変わらないということが分かって良かったです.
>実際は固有値と固有関数を求めるところまでで十分なのです. >これが分かればその系は理解できた,と言えます. これで,いままでの疑問が晴れました. 教科書が一般的過ぎて,どうしても現実味というか,実際の現象が見えてこなかったのですが,ある特別な状態まで計算すること自体,必要なかったのですね.
質問に答えてくださった方々,どうもありがとうございました.