開放電圧について
開放電圧について
ポット さんの書込 (2007/05/09(Wed) 11:39)
初めて書き込みさせて頂く，ポットと申します．
開放電圧の求め方がよく理解できず（本を読んでも理解できていない）書き込みさせていただきました．
このなかに図形を書き込めなかったため，過去ログの文書（テブナンの定理）より，参考として載っていた回路図1-2-10について．無断ですみません．
ここで，開放電圧が V0=(V1*R2 + V2*R1)/(R1 + R2) と書いてありましたが，よく理解できませんでした． また，私の持っている本では同じ回路のV0が， V0=(V1 - V2)/(R1 + R2) + V2 となっていました．どちらも同じなのですが．
２つの式の作成までの考え方を教えていただけないでしょうか？ 初歩的な質問で申し訳ないのですが，よろしくお願いします．
Re: 開放電圧について
zoro さんのレス (2007/05/09(Wed) 13:52)
ポットさん，はじめまして．
２つの理想的な電源が内部抵抗を持って，それぞれが並列として計算すればいいですよね．
いま，2つの電源が並列になっているが，外部負荷には接続していないとします．
<pre>
┌──────────────○ A
│
i,→│i,→
┌───┴────┐
││
R1R2
││
│＋ 
│＋ 
─┴──┴─
┯┯
││
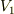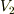└────────┴─────────○ G
</pre>
この時に，Gから見たAの電位，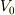 
を求めてみます．
仮に左の電源から，右の電源に流れ込む電流を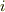 
とすると，理想的電源の両端電位差が，内部抵抗によって結合して，電流 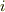が生じるのですから，
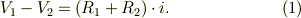
これを外の点Aで見ると，左の理想電位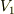 
から見れば， 
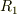による電位降下があるから；
となります．
これらの式から電流を消去すれば如何でしょう．
Re: 開放電圧について
ポット さんのレス (2007/05/09(Wed) 19:23)
zoroさん早速の返信有難うございます．
なんとなくですが判ったような気がします． 私が，電位と電圧降下の符号がよく理解できていなかったのが原因だったのだと思います．
理解が正しければ，（２）式のV0をもう一方のV2から見ると， V0 = +V2 + R2*i ということになるんですね．
zeroさんの解説非常に参考になりました． 慣れた人からは普通なのかもしれないけど，どこに視点を置くかなんかがまだ安定しない感じです；；
Re: 開放電圧について
zoro さんのレス (2007/05/09(Wed) 21:33)
＞ 理解が正しければ，（２）式のV0をもう一方のV2から見ると， V0 = +V2 + R2*i ということになるんですね． ＜
きっと，この方法でも合っていると思います．:-)
自分で作った関係式は，自分で解いて確認して下さい．今回のように，「式そのものを別解として出して，解いた結果を相互に比較する」のは一番いい方法だと思います．これは，試験でも，研究でも同じ事ですから...．
その意味では，外部に負荷を付ける為に，もう少し汎用性のある方法を書いてみます．
<pre> I3,→ ┌──────────────○ A │
I1,→│←,I2
┌───┴────┐ │J │ R1R2 ││ │＋V1 │＋V2 ─┴──┴─ ┯┯ ││ └────────┴─────────○ G
</pre>
といっても，各電源から出て来る電流の方向を，「電源から外向き」とし，電流の名前も電源ごとに換えて，更に，J点から外部に流れ出す電流を付け足しただけですが．
＊J点で「入る電流の総和＝出る電流＝０」の式を追加． ＊電位差の取り方にも工夫をする．
