ブロッホの定理 エネルギー
ブロッホの定理 エネルギー
しんす さんの書込 (2007/05/05(Sat) 21:04)
ブロッホの定理が適用できる系において,
E(k)=E(-k)
と,波数の符号を変えたものも同じエネルギーを持つことの証明をしたいのですが,どのように証明できるでしょうか?
『ハミルトニアンが時間反転に対して不変であるとき,波動関数の複素共役をとったものも同じエネルギーを持つ』ことを利用すると,
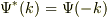
となると思うのですが理由がわかりません. 単純な見落としをしているだけかもしれませんが,何か気がつくことがありましたらよろしくお願いいたします.
Re: ブロッホの定理 エネルギー
nomercy さんのレス (2007/05/07(Mon) 05:09)
時間反転対称性からE(k)=E(-k)が言えるという観点は正しいと思います. それで
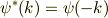
を言うにはブロッホ関数が
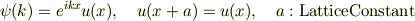
と書けるということを直接用いれば良いと思います. (簡単のためバンドは一枚だけとする) これより
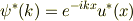
となります.これは結晶運動量が-kの状態に他なりません.つまり
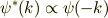
が言えました.
Re: ブロッホの定理 エネルギー
nomercy さんのレス (2007/05/15(Tue) 03:53)
しんすさん
>u(x)はkに寄らないということでいいのでしょうか?
依存します.
時間反転対称性からkと−kが同じエネルギーでなければならないという直感的な理解は納得していると思うので,以下では細かい数式を少し詳しく述べてみます. まず,現実とは違いますが理解するための最初の段階として, 「バンドは一枚だけ」 としてみます. そうすると一つの結晶運動量に対して 一つだけHamiltonianの固有状態があります.
周期境界条件の場合,結晶運動量は
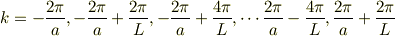
のN個の値をとり得ます.ここでLが結晶の長さ(周期境界条件の周期)であり,aが格子定数です.
以前の議論から結晶運動量がkの状態 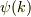 の複素共役
の複素共役 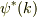 はエネルギーが同じ状態でした.
また,結晶運動量が-kであることも分かっています.
今,仮定から一つの結晶運動量に対して一つだけHamiltonianの固有状態があるので,
はエネルギーが同じ状態でした.
また,結晶運動量が-kであることも分かっています.
今,仮定から一つの結晶運動量に対して一つだけHamiltonianの固有状態があるので, 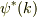 はエネルギーがE(k)の状態でなければなりません.
ここから逆に
はエネルギーがE(k)の状態でなければなりません.
ここから逆に
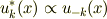
でなけれなならないことになります.
こうしてバンドが一枚しか存在しない場合にはkと−kは同じエネルギーを持っていることが分かりました.
「バンドが一枚という状況には納得出来ん!」
という場合には一般にバンドが沢山ある場合に上と同様に考えてみて下さい.