摩擦力の問題について.
摩擦力の問題について.
こうじろう さんの書込 (2007/05/02(Wed) 22:55)
こんばんは.浪人生です. 先日摩擦に関して質問をしたものです. その折は親切な回答ありがとうございました.
みなさまからわかりやすい解説をしていただき, その後摩擦力に関する類題を自分でといていました.
ところが,わからない問題がでてきてしまいました. よろしければ,解説お願いします. 出典は,河合出版浜島清利の物理のエッセンス力学45の問題です.
問題文は,滑らかな床上に,質量m,MのA,Bを重ねておき, 静止状態からBをF1の力で引くと,AはBの上を滑った. はじめAがBの左端からlの距離にあったとすると,何秒後にAはBから落ちるか. A,B間の動摩擦度係数をuとする.
この問題の解答では,AはBに対して左にすべるから,動摩擦力umgを右向きに受ける. すると,Bはその反作用を左向きに受ける.
この後の計算は運動方程式を立式をしてとくんですが,最初は間違っていましたが,その後の過程はあっていました. それで僕が間違えたところは,最初のところです.
皆さんの解説を参考にしながら自分なりにまず,左向きにAが動いた(滑った)ことから左に力がかかるような推進力があるはずだと考えて,Aに左向きの摩擦力がかかり,作用反作用の関係からBに右向きの摩擦力があるとしてときました. しかし,摩擦力はまったく逆でした.
僕の考えどこがおかしいんでしょうか? どうかお願いします.
Re: 摩擦力の問題について.
ミュフ猫 さんのレス (2007/05/02(Wed) 23:21)
>左向きにAが動いた(滑った)ことから左に力がかかるような >推進力があるはずだと考えて
これはBの観測系においてですよね?静止系(慣性系)で考えるべきでは? そうすれば,Aは右にしか動きようがないことが解かるのではないでしょうか. 私は,昔,摩擦力の向きは気にしませんでした. 正しい方程式さえ立てられれば,後から符号で向きが判別できますから.w でも,常にイメージを描こうとする事は,物理学を学ぶ学生としては, 絶対に必要な取り組みだと思います.
Re: 摩擦力の問題について.
zoro さんのレス (2007/05/03(Thu) 02:19)
確かに計算しようとすると,混乱しそうですね.
こういう場合,とりあえず絵を描きましょう.
<pre>
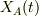 |
v___________
| |
| A: m=M_A |
______|__________|________
| |
| B: M=M_B |---> F1
|_________________________|
---------+--------------------------------------------->x
O(原点オウ) ^
|
|
v___________
| |
| A: m=M_A |
______|__________|________
| |
| B: M=M_B |---> F1
|_________________________|
---------+--------------------------------------------->x
O(原点オウ) ^
|
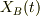 </pre>
</pre>
其々の物体の左端を,静止座標系(当然,慣性系)から計るとします.題意より,t=0で,

なお,計算間違えをなくす為に,質量を下付き添え字で区別します.
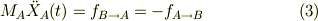
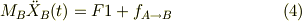
●F1が十分に小さい場合●
AとBにはすべりを生じないから,
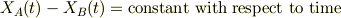
故に,
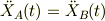
この式の為に,式 (3,4) を辺々加えると
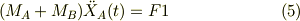
ここで
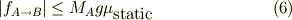
●F1が大きい場合●
Bに外力F1が加わりBが動くが,Aの摩擦により,Bの運動は減少するから,式(4)において,
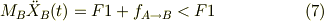
故に

当然,
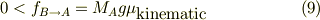
式(3)から
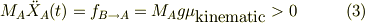
当然,
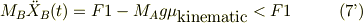
Bから見たAの相対座標を考える;
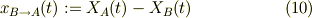
式(3,7')から
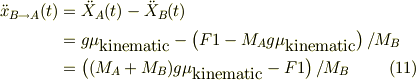
こんな感じでは?
Re: 摩擦力の問題について.
こうじろう さんのレス (2007/05/03(Thu) 13:53)
>>ミュフ猫さん レスありがとうございます.
>これはBの観測系においてですよね?静止系(慣性系)で考えるべきでは? >そうすうれば,Aは右にしか動きようがないことが解かるのではないでしょうか.
ここのところがよくわかりません. そもそも観測系と静止系の違いは何なんでしょうか. また,静止系でなぜ考えなければいけないんでしょうか. 静止系で考えたら,なぜ右にしか動きようがないんでしょうか.
もうすこし,この3点を解説願えないでしょうか
昔は摩擦力の向きを気にしてなかったんですか?笑 運動方程式を立てる場合でもどちらを引くかで答えがかわってくるんではないんですか? はい確かにイメージをわかせるために,図を描いたり,資料集をよくみたりしています. 資料集なんて特に日常生活との話をリンクさせていて面白いです笑
>>zoroさん レスありがとうございます.
わざわざ,図まで描いたりしてくださってありがとうございますw これ大変だったんじゃないんですか?w ここまでしてくださるとは,感謝感激です.
ただ言いにくいんですが,高校の物理の問題で座標系で考えたこともなく, そのように解説してくださった先生方もいなかったので, 式のいたるところで理解できないところがでてきてしまいましたw
Re: 摩擦力の問題について.
zoro さんのレス (2007/05/03(Thu) 15:28)
>ただ言いにくいんですが,高校の物理の問題で座標系で考えたこともなく, >そのように解説してくださった先生方もいなかったので, >式のいたるところで理解できないところがでてきてしまいましたw
貴重なご意見有難うございます.
高校の教科書,物理と数学の今年度用を手に入れたものの,まだ詳しく読んでいません.
もし宜しければ,「河合出版浜島清利の物理のエッセンス力学45」の入手方法を教えていただけませんか?
Re: 摩擦力の問題について.
ミュフ猫 さんのレス (2007/05/03(Thu) 17:14)
>そもそも観測系と静止系の違いは何なんでしょうか.
デカルト座標を設定する場合,原点に定めた位置が絶対静止空間に対して, 相対的にどのような運動をするかで,静止系(慣性系)か否かが決まると 思います.この辺の議論は,プロかセミプロの人にでも聞いてください. 私には荷が重いです.w
>また,静止系でなぜ考えなければいけないんでしょうか.
考えるべき(should think)と思うだけで,いけないことは無いかと. 非慣性系(加速度系)で考えると,慣性力を考慮しなければならず, イメージが取りにくくなるので,私は出来るだけ静止系で考えます.
>静止系で考えたら,なぜ右にしか動きようがないんでしょうか.
もし,静止系でAが左に動くと仮定すれば,作用反作用の法則から, BはAから右向きの動摩擦力を受けることになり,Bが受ける外力の 総和の右方向成分が,F1よりも大きくなるからです. F1で引っ張るのに,F1より大きな力で引っ張られたときのような 加速度運動をするのは,ニュートン力学の法則に反するかと.
どなたか,助け舟出してください.(ToT)
Re: 摩擦力の問題について.
toorisugari no Hiro さんのレス (2007/05/03(Thu) 18:29)
こうじろうさんは,摩擦を運動に対する抵抗と理解されているようですが,間違いです.
ただしくは「相対」運動に対する抵抗です.
「動いている」というとき「何に対して」動いているいるのかを言わないと意味がありません.
こうじろうさんは「Aの物体が動いている」というとき,地上にたった目で判断しています.「右向きにうごいている」と.
しかし,摩擦は接触する物体の相対的な速度(速度差)が大事なのです.
Bから見たAの速度(左向き)でかんがえないといけません.
右向きに等速度運動する物体Bの上に物体Aを同じ速度で置いたとき,Aには動摩擦力も静止摩擦力も働きません.こうじろうさんはAに静止摩擦力がかかっていると思っておられるのではないでしょうか?
摩擦は接触面の恒常的なズレ,あるいはズレを生む作用,に抵抗する力です.
Re: 摩擦力の問題について.
なんとなく さんのレス (2007/05/03(Thu) 20:06)
横やりですが,こうじろうさんの思考過程を振り返ってみると,やはり運動の3法則をもう一度押さえておく必要があると思います.迷うときは原点に戻るのが一番です.私の理解は下のようです. 以下で右左は止まって観測している私に向かって,とします.まず,問題設定の「滑らかな床」はいいですね.物体Bと床には摩擦が働かないことを言うわけですね.物体AはBの上にあり,かつ,つながっていないのですが,AはBにAの重さ分の力を鉛直(重力方向)に及ぼし,その結果,AはBから反作用で同じ大きさの垂直抗力を受けています.ここで,Bが水平に(右向きに)力F1で引っ張られ,動き始めたとします.もし,AとBに摩擦が無ければどうなりますか. AはBから(水平方向の)力を受けることができず,取り残されて(元の位置のまま)真下へ落下します.これは「慣性の法則」です.摩擦がある今の場合,F1がAとBの(間の)静止摩擦より小さければ,Aは(比喩的に言えば)止まっていたいのに,Bからの摩擦力(ここも間違い易いですが,相対的に静止していても,力を静止摩擦力によって互いに及ぼし合っています)によって同じ方向に力を受け,Bと同じ向きに動き始める筈です.Bにはその反作用でF1と反対向きの力を受けますが,このため,B(とA)の加速度はB単体であるよりも小さくなります.これはAとBが一体となってF1という力を受けたとして求めた加速度と一致します.それではF1が最大静止摩擦(力)より大きければどうでしょう.Aは右方向へ運動しているものの,Bにはついて行けず,Aが一端動き始めれば摩擦は動摩擦となり,動摩擦は静止摩擦より一般に小さいため,ますます取り残されます.これがBに対して逆向きに運動しているように見えるということです.問題設定はこれらのことが一瞬の内に起こった後のことであると見ていいでしょう.このとき,動摩擦(力)はAにとってAの(Bに対する)運動を妨げる方向(向かって右)へ働きます.なぜなら,それは上記の一体となって動くときと本質的には同じ力だからです.摩擦の向きが変わるわけではないのです.その反作用はやはりBの加速度をB単体のときよりは小さくさせるでしょう. 今までの中で,運動の第2法則,第3法則が一体となって使われているのに気づかれたでしょうか.この問題は摩擦という現象を通じた上記3法則の理解,特に慣性の法則の理解を問うているものと言っていいでしょうね. 蛇足ながら,「だるま落とし」はこの問題のF1が大きくかつ瞬間的に与えられた場合のケースに近いと言えると思います.
Re: 摩擦力の問題について.
komagatake さんのレス (2007/05/03(Thu) 21:43)
摩擦力の向きについてです.
座標系という考え方は高校生には難しいです.
摩擦がないとしたらどういう運動をするかを考えるといいと思います.
Bの上にAが乗っていてBだけを右にひっぱります.摩擦がなければBだけが動いてAはそのまま下に落ちます.下にあったBがなくなるので真下に落ちます. 摩擦があればいくらか引っかかるわけですから引きずられます.でもBの動きには付いていけません.いくらか遅れます.Bと一緒の運動をする場合は張り付いているときです. Bの動きには付いていけないのですから少し右に運動して下に落ちてしまいます.左に動いているのではありません.右に動いているBの上にいる人から見ると後ろに滑っているように見えますが机の上の人から見ると右に動いています.Bの動きに付いていけないので下に落ちるわけです. AもBも初速度はゼロです.右に動く加速度の大きさが違います.Bの方が大きいのです.Aに働く力は右向きに働いている摩擦力です.Bに働く力は右向きに加えられた力と左向けに働いている摩擦力です.Aに働いている右向きの摩擦力とBに働いている左向きの摩擦力は作用・反作用の関係にあります.
こういうので分かりますか.
Re: 摩擦力の問題について.
こうじろう さんのレス (2007/05/04(Fri) 17:19)
こんにちは. レスありがとうございました.
昨晩みなさんのレスを参考にしながら整理してみました まずは,おっしゃるように, Fが静止摩擦力より小さい場合→AとBがくっつく. これは前回僕が質問した問題だったんですが,相関性があったんですね.
Fが静止摩擦力より大きい場合→AとBがすべる
いろいろな説明があって混乱してしまいますが,まとめとしては, 摩擦力の向きを考えるときは,摩擦力をないものとして考えて他の力がない場合は題意の動くように摩擦力が形成されるはずだと考える. または,この問題のように重なっている場合は外から見た視点ではなく,AとBの接触面の動き,つまり右に動いているBの人からみてAが動いている方向の逆方向に擦力がかかる. これらのどちらかによって摩擦力の向きを決定した後は, 図を書いてみてイメージを膨らませる. という感じでいいでしょうか?
ちなみによく物理では,見る場所によって物体の動き方が違って見えますがこういう問題のときってどうイメージしているんですか? 自分は実際にはBの上にはいないじゃないですか…
それと,このような問題を解くときのみなさんの思考の流れをすこし箇条書きとはいいませんが,矢印などを使って書きあらわしていただけませんか. まとめとして参考にしたいんでどうかよろしくお願いします.
>>zoroさん このエッセンスという本は高校物理の参考書?としてはかなり有名な本なので,高校生用の参考書売り場にはどこでにもあると思います. 一応アマゾンへのリンクをはっておくでの,よろしかったらみてください.
ちなみに下もあって,そちらは原子物理・熱・電磁気になっています.
ともあれ,自分の考えをまとめ,みなさんの回答を考えながらこの文章をかいていたら,頭が悪いせいか1〜2時間時間ぐらいかかってしまいました笑 物理だけ考える日というのも何か乙なものですね,ぞっと疲れますがw
Re: 摩擦力の問題について.
zoro さんのレス (2007/05/04(Fri) 19:48)
こうじろうさん,
アマゾンへのリンクをご紹介くださり有り難うございました.
>出典は,河合出版浜島清利の物理のエッセンス力学45の問題です.
これを「物理のエッセンス力学45」とい本と勘違いしていました.本屋さんで眺めてみます.
まずは,正統的に教科書を拝見します.自分は,数学は教科書に従って勉強したのですが,物理は,ゴーイング・マイ・ウェイだったので,昔との差が判りません(泣).
Re: 摩擦力の問題について.
komagatake さんのレス (2007/05/04(Fri) 21:59)
>自分は実際にはBの上にはいないじゃないですか…
私はこの問題の場合,机と同じ場所でA,Bの運動を見ているという立場です.Bの上に乗った立場で見ると混乱します.A,Bを外から見ているというのが出来たうえでBの上に乗っている立場ではどの様に見えるかを考えます.見る立場を変えるとどの様に見えるかは力学では重要な考え方だと思います.実際に可能な立場は片方かも知れませんがその立場であればどの様に見えるかが分かるというのは大きいことです.地球が太陽の周りを回っている図を今では小学生でも書きます.誰も地球と太陽を見ることが出来る場所に行った事がないはずです.天動説と地動説です.どちらも間違ってはいません.見る立場によって違って見えるという運動の記述の違いでしかありません.見えたままが実体に近いかどうかは別問題です.
相対運動は見る立場の違いによって運動の表現がどの様に変わるかを表しています.その前提にどの立場も同等であるという考えが入っています.力学法則は等速度で運動しているものの間では違いは出てきません.地球が動いていることを意識しないで生活し,力学を考えることが出来るのです.ガリレオの相対性といいます.これは力学的世界観の一つだと言ってもいいくらいです.でもこの見方が出来るためには練習が必要です.
今でも表現の方法としては天動説を使っています.宇宙の中の地球という立場が必要なときは地動説を採りますが地球の上でのことしか問題にならなければ天動説で十分です.気象学がその代表だと思います.
今の高校の物理では運動全体を出来るだけ外から見ようとしています.円運動も外から見ていますから向心力しか出てきません.遠心力,向心力と2つ出てくれば混乱するのが目に見えています.
電車が加速するときにつり革が後ろに傾くというのも電車を外から見た立場で考えます.以前は電車の中の人が見たときという立場と両方出てきていましたが今は一つです.(これは今回の摩擦の問題と事情が似ていると思います.つり革は電車の動きに付いていけなくて遅れます.それが傾く理由なんですがそのように考えることが出来ますか.)
>ともあれ,自分の考えをまとめ,みなさんの回答を考えながらこの文章をかいていたら,頭が悪いせいか1〜2時間時間ぐらいかかってしまいました
1〜2時間考えるというのは普通です.考えながら文章を書いていれば時間がかかります.だから逆に文章を書くことによって考えがまとまってくるということも起こるのです. 私にしてもこれだけの文章を書くのにかなりの時間を使っているのですよ.ささっと書くことが出来るというものではありません.それだけ時間をかけていても意味不明な文章がまぎれ込んでいる場合もあるのです.
Re: 摩擦力の問題について.
なんとなく さんのレス (2007/05/05(Sat) 09:00)
>komagatakeさん
どういたしまして.逆に,同じ考えの方がいらして安心しました.
>こうじろうさん
イメージの多くは体験に基づく想像力です.この体験とは,読書や映像あるいは人の会話でさえも含む幅広いものを指しています.そのような素養をデータベースとして自分の中に蓄積していく,つまり普段から何でもないようなことを自分の発想で考えてみる訓練が大事であると思います.