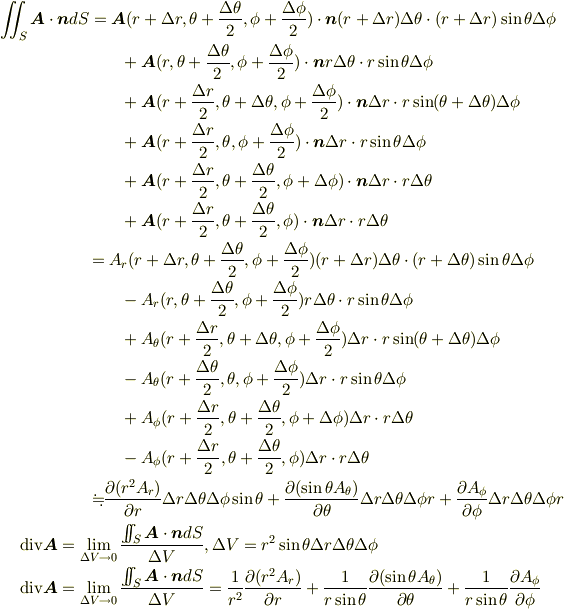divについて
divについて
tip★ さんの書込 (2007/05/02(Wed) 17:57)
直交座標系でのdivEの計算 1,divE=dE(x)/dt+dE(y)/dt+dE(z)/dtを証明せよ. 2,極座標系でのdivEを求めよ.
自分は,一応1番の問題は自力で解けたのですが,2番目の問題が分かりません. 1番では?V=?x?y?zを作って,各辺からの湧き出しを計算したのですが,2番目はどのような微笑体積を作って湧き出しの計算をしたらいいのか,混乱してしまって分かりません.
どのたか解説よろしくお願いします.
Re: divについて
toorisugari no Hiro さんのレス (2007/05/02(Wed) 18:40)
問題1.自体が意味不明なのですが....
完全な問題(  の正確な定義)を書いてください.
の正確な定義)を書いてください.
単に発散の極座標表示を求めよという問題でも,いろいろなやり方があり,しかも,長いので,tip★さんの予備知識を教えてもらえないと(ex. divはどのような定義で理解してるかとか,gradの極座標表示はできるとか,Gaussの定理は理解しているとか),説明できません.
とりあえず,予想して聞きますが,
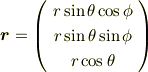
としたとき, 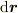 を
を
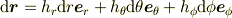
とできますか?これがわかれば,比較的簡単に計算できます.
# かぎしっぽに座標変換の解説,ありましたっけ?ぱっと見,探せなかったんですけど >staffさま
Re: divについて
tip★ さんのレス (2007/05/02(Wed) 19:07)
申し訳ありません.
この問題は大学の講義中,先生が自分でやっときないさいと言われた問題ですので,特にどの問題集からでたという問題ではありません.
Eは電場のことです.E(x),E(y),E(z)は,それぞれEのx成分,y成分z成分です. dE(x)/dtとなっていますが,偏微分のことです.
divE=(Eの面積分)/?V (?V→0) で習いました. gradVの極座標表示はできません. ガウスの定理は一応理解しているつもりです.
自分は,今工学部の大学2年生です.電磁気学は1年生のとき一通りマクスウェルの方程式までやっています.
よろしくお願いします.
Re: divについて
toorisugari no Hiro さんのレス (2007/05/02(Wed) 19:18)
つまり,こういう問題なのですね.
「
1. 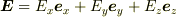 として
として 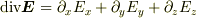 を示せ.(ただし,
を示せ.(ただし, 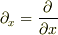 .
. 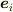 はi方向の単位ベクトル.)
2.
はi方向の単位ベクトル.)
2. 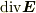 の極座標表示をもとめよ.
」
の極座標表示をもとめよ.
」
じゃ,先に聞いた
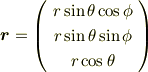
としたとき,
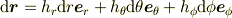
となるのはできますか?これがわかれば,それぞれの微小ベクトル( 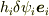 )が張る直方体で考えればよいです.
)が張る直方体で考えればよいです.
Re: divについて
tip★ さんのレス (2007/05/02(Wed) 19:38)
申し訳ありませんん.hというのがよくわかりません.
1番の問題は, 領域Vとして6つの平面を境界とする直方体について考える. V=?x?y?z (Eの面積分)=[Ex(x+?x,y,z)-Ex(x,y,z)]?y?z+・・・ →(dEx/dt)?x?y?z+・・・ (途中省略) divE=(1/?x?y?z)(Eの面積分) (?x?y?z→0)=dEx/dt+dEy/dt+dEz/dt というようなやり方をしました.今度はExがEのx成分です.
できれば,これと同じようなやり方で解説してくれたら,うれしいです.
よろしくお願いします.dE(x)/dt+dE(y)/dt+dE(z)/dt
Re: divについて
toorisugari no Hiro さんのレス (2007/05/02(Wed) 19:44)
> これと同じようなやり方で解説してくれたら,うれしいです.
そのつもりですよ.
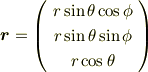
としたとき
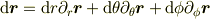
はわかりますか?
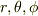 が
が  の関数として
の関数として
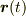 を
を  で微分してみてください.
で微分してみてください.
(時間がないのでここまでにさせてください.あとは他の方お願いします. 3個の微小変位ベクトルが直方体をなすことと各辺の長さがわかれば各面の面積積分を近似計算でだして,和(差)を直方体の体積でわれば目的のものが得られます.)
Re: divについて
tip★ さんのレス (2007/05/02(Wed) 20:06)
すみません.がんばってみましたが,ちょっと分かりません.
ベクトルの微分はまだしたことがありません.
そこのところを解説してもらえれば,うれしいです.
よろしくお願いします.
Re: divについて
Re: divについて
toorisugari no Hiro さんのレス (2007/05/02(Wed) 21:08)
出先のPHSからなので,あまり書き込めません.
先ほど「直方体」と書いたのは間違いです. 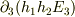 から
から 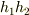 が出ては困りますね.
が出ては困りますね.
Johさんのページに書いてあることがやりたいことです.よろしくお願いします>Johさん.
Re: divについて
zoro さんのレス (2007/05/03(Thu) 03:05)
tip★さん,横から失礼します.
もし,極座標表示のパラメータ( 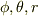 ) とその接線である基底ヴェクタ(
) とその接線である基底ヴェクタ( 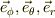 ) との幾何学的関係が把握できているならば,其々の基底ヴェクトルに垂直な微小断面が,微分変化をするとして力技で計算はできます.
) との幾何学的関係が把握できているならば,其々の基底ヴェクトルに垂直な微小断面が,微分変化をするとして力技で計算はできます.
図を書けば,容易に判りますが,デカルト座標では,相対する微小面積素は等しくなります.例えば 基底ヴェクトル, 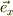 方向の微小面積素は
方向の微小面積素は 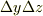 で,xの値によらず一定です.
で,xの値によらず一定です.
しかし極座標では,対応する基底ヴェクタ( 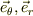 ) に対応する微小面積素は,それぞれの変数,(
) に対応する微小面積素は,それぞれの変数,( 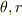 )の関数になるので,その分を考慮する必要があります.
)の関数になるので,その分を考慮する必要があります.
他方, 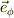 の方向にたいする微小面積素は,
の方向にたいする微小面積素は,  に依存しないので,デカルト座標と同じ扱いが出来ます.
に依存しないので,デカルト座標と同じ扱いが出来ます.
他の方々のようにエレガントな方法ではありませんが...(笑).でも,幾何学的に微量線素,微量面積素を出しているだけで,解析的な計算と,本質的には同じです.
Re: divについて
tip★ さんのレス (2007/05/03(Thu) 13:07)
ちょっと自分では理解できませんでした.
- http://radphys4.c.u-tokyo.ac.jp/~k-komaki/kougi/ans04-1a.pdf#search= '%E7%90%83%E5%BA%A7%E6%A8%99%20%20%E3%83%99%E3%82%AF%E3%83%88%E3%83%AB%E8%A7%A3%E6%9E%90%20div%20%E8%A8%BC%E6%98%8E'
↑ここに,自分が求めてる解答があるのですが, なぜ,このような微小体積を考えるのか,なぜ各辺の微小面積がこのようになるのか,が理解できません.
どのたか,解説お願いします.
Re: divについて
zoro さんのレス (2007/05/03(Thu) 13:38)
tip★さん,
どこが,どう,判らないかを示されないと説明しにくいですね.
例えば,上に示された回答は,先に自分が書いた概略説明と類似だと思います.そこで,tip★さんが極座標をどこまで理解しているかと,デカルト座標での証明を何処まで理解されているかが鍵になるように思いました.
もし極座標になれていない場合,上のpdfをいくら眺めても駄目ではないかと思います.
Re: divについて
tip★ さんのレス (2007/05/03(Thu) 15:57)
すみません.
ここで説明するには限界があるし,高等な数学を使っているので,本で調べることにしました.というか,なんかきちんと勉強してこないと,自分には敷居が高すぎるように感じました・・・
(多分この問題を出した先生は,上のような高等な数学を用いたやり方を求めていないと思います.)
Re: divについて
toorisugari no Hiro さんのレス (2007/05/03(Thu) 18:08)
もうたぶんいらっしゃらないとおもいますが,
> (多分この問題を出した先生は,上のような高等な数学を用いたやり方を求めていないと思います.)
というより,tip★さんが微分,特に偏微分を全然理解されていないのが一番の原因だと思います.
# divの記法を見る限り,そう思います.
正直,偏微分を理解せずにどうやってMaxell eq.を勉強されたと言えるのか興味がありますが,まず,微積の(簡単な)教科書で偏微分まで理解されることをおすすめします.
Re: divについて
tip★ さんのレス (2007/05/03(Thu) 18:37)
解決しました!みなさんありがとうございました.
上のような難しいやり方はしなくてもいいみたいです.
>># divの記法を見る限り,そう思います.
本当の記法はどのようなものになるのでしょうか?教科書には上のような式がありました.
>>正直,偏微分を理解せずにどうやってMaxell eq.を勉強されたと言えるのか興味がありますが,
大学1年生で,しかも工学部の学生が学ぶマクスウェル方程式というのはそんなレベルということでしょう・・・正直,偏微分は計算できれば,それでいいという感じに教えられているので,厳密な所の理解はできていません.もう1回勉強しなおしたいと思います.
Re: divについて
toorisugari no Hiro さんのレス (2007/05/03(Thu) 19:09)
> 解決しました!
よかったですね.
> 上のような難しいやり方はしなくてもいいみたいです.
今後の参考のため,その方法を教えてもらえないでしょうか?
>># divの記法を見る限り,そう思います. > 本当の記法はどのようなものになるのでしょうか?教科書には上のような式がありました.
あれが偏微分とはとても思えません.どう見ても  (時刻?)についての常微分です.
よく使われる記法は
(時刻?)についての常微分です.
よく使われる記法は 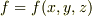 に対して,例えば
に対して,例えば
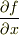 ,
, 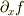 , ∂f/∂x
です.
, ∂f/∂x
です.
また,その教科書の書籍名と著者名および出版社名を教えてください. 本当に偏微分の意味であの記法を使っているのなら驚きです.
Re: divについて
tip★ さんのレス (2007/05/03(Thu) 19:31)
>>今後の参考のため,その方法を教えてもらえないでしょうか?
zoroさんのやり方と多分同じだと思います.ただよくわからない数学が出てきたので,何を言いたいのかよく分かりませんでした.
>>あれが偏微分とはとても思えません.どう見ても(時刻?)について常微分です. >>よく使われる記法はすでに示していますので見てください.
>>また,その教科書の書籍名と著者名および出版社名を教えてください. >>本当に偏微分の意味であの記法を使っているのなら驚きです.
えーーと,「divについて」のところを全部読めば分かると思うんですが,自分はTexの使い方がよく分からないので,dEx/dtを偏微分とみなしているだけです.
Re: divについて
toorisugari no Hiro さんのレス (2007/05/03(Thu) 19:42)
> zoroさんのやり方と多分同じだと思います.
たぶん, 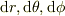 動かしたときにできる直方体の各辺が
動かしたときにできる直方体の各辺が 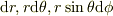 となることを絵で示したものじゃないですか?
それなら,みなさんおなじことをいっていますよ.
となることを絵で示したものじゃないですか?
それなら,みなさんおなじことをいっていますよ.
> 自分はTexの使い方がよく分からないので,dEx/dtを偏微分とみなしているだけです.
TeXの問題というより数学力の問題に思えます.
先に示したように div E= ∂Ex/∂x+∂Ey/∂y+∂Ez/∂z と書くか,せめて div E= dEx/dx+dEy/dy+dEz/dz (dは偏微分) と書くべきですね.
Re: divについて
tip★ さんのレス (2007/05/03(Thu) 20:10)
直方体??直方体じゃないですよ・・・直方体に近似してるんですか?
>>div E= dEx/dx+dEy/dy+dEz/dz (dは偏微分) >>と書くべきですね
よく読んでください!書いてますよ! 少なくとも普通の微分と偏微分は間違えないですよ!
Re: divについて
toorisugari no Hiro さんのレス (2007/05/03(Thu) 20:23)
> よく読んでください!書いてますよ! > 少なくとも普通の微分と偏微分は間違えないですよ!
> 1,divE=dE(x)/dt+dE(y)/dt+dE(z)/dtを証明せよ.
よく読みましたが,正しく書いておられないし,「普通の微分と偏微分は間違え」というより「微分」そのもの,あるいはdiv,を理解されていないようにお見受します.
Re: divについて
zoro さんのレス (2007/05/03(Thu) 20:29)
みなさん,
大昔,計算した方法をいま再現中です.ごり押し方式なので,式が複雑になり苦戦しています.
#昔は, 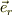 方向の微小面積素の計算だけでお茶を濁したのを思い出しました(笑).
方向の微小面積素の計算だけでお茶を濁したのを思い出しました(笑).
でも,私みたいに,数学が弱い人間にとって,幾何学的な関係を見ながら計算が進むのは,結構楽しい所でもあります.もうしばらく掛かりそうですが,出来たらアップします.しばらくご容赦を.
Re: divについて
toorisugari no Hiro さんのレス (2007/05/03(Thu) 20:43)
> 直方体??直方体じゃないですよ・・・直方体に近似してるんですか?
あ,バームクーヘン状の形状の事ですか?それなら直方体というよりそういった方が適切ですね.もっとも,体積の計算の時に直方体に近似しますが.
それとも,暗黙の対称性を導入して,輪とか殻状の幾何に対して計算しているのかな?
Re: divについて
tip★ さんのレス (2007/05/03(Thu) 20:54)
>>よく読みましたが,正しく書いておられないし,「普通の微分と偏微分は間違え」というより「微分」そのもの,あるいはdiv,を理解されていないようにお見受します.
下のほうに訂正をしているということです. あと,人の言っているのことをもうちょっと汲み取ってほしいです.たとえば,dE(x)/dtのところは偏微分の記号が見つけられなかったんだな,とか,げんにほかの人は汲み取ってくれてます. あと,厳密性を気にするのはわかるのですが,そんなことでバカ扱いされるのは心外です.
Re: divについて
zoro さんのレス (2007/05/03(Thu) 21:23)
tip★さん,
私は,この計算の一部を,1年生の後期に数学の出来る友人と論争した事があります.その人は,変数の変換として解析的に計算するように主張されました.今回の説明をされた方々と同じです.それに対して,幾何学的にやる方が,面倒だがイメージができるからといって,今回の計算をしました.当時はパソコンがなく,数式を手書きでするので,何度も間違えて,動径方向の計算だけ出来たと思います.
その計算結果を見せると,その友人は,物理的なイメージの大切さを理解してくれました.他方,彼は逆に,hパラメータの便利さを目の前で見せてくれましたが,私は,意固地に公式集を使えば良いと主張して,今日に至りました.
今回,このような計算をフルに出来たのは,パソコンから数式を書けたのがなんといっても一番の理由だとおもいます.書き出しは,ノートとの食い違いを確認するので混乱しますが,途中から整理が付き出すときの快調さは素晴らしいですね, LaTeXの強みを感じる一瞬です.
と,同時に,こんな計算は,二度としたくないので,解析的な方法論を習得しようと思います.tip★さんは,お若いのですから,夏休みなどに,解析的な方法を学ばれるのも良いかもしれませんね.
■■■■■■■■■■■■■■■■■■■■■■■■■■ ■■目標:ヴェクタ場の発散を極座標で表したい■■ ■■■■■■■■■■■■■■■■■■■■■■■■■■
直感的に論議を進めて見ます.極座標の図は書けませんが,Johさんが示された
の図に準じます.
まずは,この極座標で座標パラメータ( 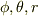 )を変えていくと,位置がどのように変わるかを考えます.
)を変えていくと,位置がどのように変わるかを考えます.
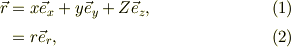
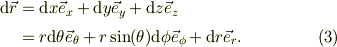
ここで極座標の基底ヴェクタ( 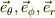 )は相互に直交して,単位長とします.
)は相互に直交して,単位長とします.
■■■ 微小6面体の要素 ■■■
計算の簡便性の為に,式(3)を見て,其々の基底の方向についての微小線素を定めます;
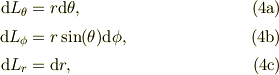
当然;
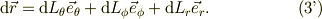
点 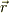 から上記の微小線素をがつくる微小体積の体積素;
から上記の微小線素をがつくる微小体積の体積素;
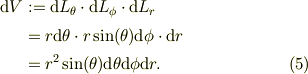
また,点 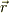 から上記の極座標の基底ヴェクタが向く方向の微小面積素を次に定める.
から上記の極座標の基底ヴェクタが向く方向の微小面積素を次に定める.
まず,  の増加方向,
の増加方向, 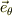 の微小面積素ヴェクタ;
の微小面積素ヴェクタ;
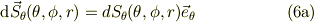
ここで,
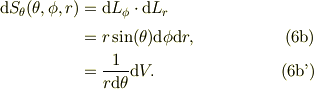
この微小面積素の対抗面は上式より,mbox{d}thetaの高次の項は切り捨てます.
#ある変数の微分は1次までとするわけです. #これは,外微分形式の計算の特徴でもあります.
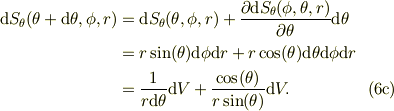
同様に,  の増加方向,
の増加方向, 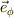 の微小面積素ヴェクタ;
の微小面積素ヴェクタ;
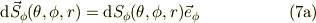
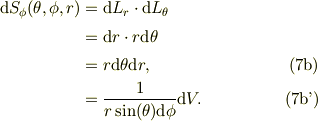
この微小面積素の対抗面は上式より,
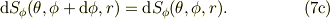
さらに,  の増加方向,
の増加方向, 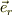 の微小面積素ヴェクタ;
の微小面積素ヴェクタ;
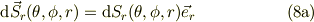
ここで,
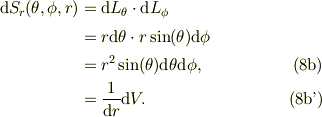
この微小面積素の対抗面は上式より,
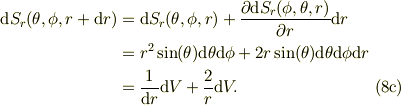
■■■ ヴェクタ場 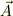 とその発散 ■■■
とその発散 ■■■
ヴェクタ 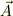 が,場を示すとすれば,位置のヴェクタ
が,場を示すとすれば,位置のヴェクタ 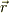 の関数で決まった値を持つことです.
の関数で決まった値を持つことです.
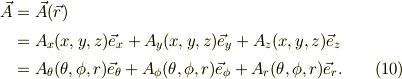
なお,極座標で計算する場合,簡略して;
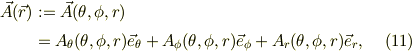
とも書く事にする.
このようなヴェクタが,先に述べた微小6面体の面を,内部から外部に向いて出るときに,微小6面との微小面ヴェクタとの内積の和を微小体積素で割ったものとする.
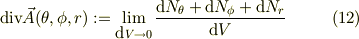
ここで,
![\mbox{d}N_{\theta} &:= +\vec A(\theta +\mbox{d}\theta, \phi, r)\cdot \left(\mbox{d}\vec S_{\theta}(\theta +\mbox{d}\theta, \phi, r)\right) +\vec A(\theta, \phi, r)\cdot \left(-\mbox{d}\vec S_{\theta}(\theta, \phi, r)\right) \\&= +A_{\theta}(\theta +\mbox{d}\theta, \phi, r)\mbox{d} S_{\theta}(\theta +\mbox{d}\theta, \phi, r) -A_{\theta}(\theta, \phi, r)\mbox{d} S_{\theta}(\theta, \phi, r)\\&= \left[A_{\theta}(\theta, \phi, r)+ \frac{\partial A_{\theta}(\theta, \phi, r) }{\partial \theta}\mbox{d}\theta \right] \left(\frac{1}{r\mbox{d}\theta}\mbox{d}V +\frac{\cos(\theta)}{r\sin(\theta)}\mbox{d}V \right) -A_{\theta}(\theta, \phi, r)\frac{1}{r\mbox{d}\theta}\mbox{d}V\\&= \frac{\partial A_{\theta}(\theta, \phi, r) }{\partial \theta}\frac{1}{r}\mbox{d}V +A_{\theta}(\theta, \phi, r)\frac{\cos(\theta)}{r\sin(\theta)}\mbox{d} V\\&= \frac{1}{r\sin(\theta)}\frac{\partial \left[ \sin(\theta)A_{\theta}(\theta, \phi, r) \right]}{\partial \theta}\mbox{d}V. \tag{13}](http://hooktail.maxwell.jp/bbslog/93be3aa466c60dd7a4691df1de374bc2.png)
また,
![\mbox{d}N_{\phi} &:= +\vec A(\theta , \phi+\mbox{d}\phi, r)\cdot \left(\mbox{d}\vec S_{\phi}(\theta, \phi +\mbox{d}\phi, r)\right) +\vec A(\theta, \phi, r)\cdot \left(-\mbox{d}\vec S_{\phi}(\theta, \phi, r)\right) \\&= +A_{\phi}(\theta, \phi +\mbox{d}\phi, r)\mbox{d} S_{\phi}(\theta, \phi +\mbox{d}\phi, r) -A_{\theta}(\theta, \phi, r)\mbox{d} S_{\phi}(\theta, \phi, r)\\&= \left[A_{\phi}(\theta, \phi, r)+ \frac{\partial A_{\phi}(\theta, \phi, r) }{\partial \phi}\mbox{d}\phi \right] \left(\frac{1}{r\sin(\theta)\mbox{d}\phi}\mbox{d}V \right) -A_{\theta}(\theta, \phi, r)\frac{1}{r\sin(\theta)\mbox{d}\phi}\mbox{d}V\\&= \frac{\partial A_{\phi}(\theta, \phi, r) }{\partial \phi} \frac{1}{r\sin(\theta)}\mbox{d}V\\&= \frac{1}{r\sin(\theta)}\frac{\partial A_{\phi}(\theta, \phi, r)}{\partial \phi}\mbox{d}V. \tag{14}](http://hooktail.maxwell.jp/bbslog/51a48b8602c3d84cbe798787653a8460.png)
最後に,
![\mbox{d}N_{r} &:= +\vec A(\theta , \phi, r+\mbox{d}r)\cdot \left(\mbox{d}\vec S_{r}(\theta , \phi, r+\mbox{d}r)\right) +\vec A(\theta, \phi, r)\cdot \left(-\mbox{d}\vec S_{r}(\theta, \phi, r)\right) \\&= +A_{r}(\theta , \phi, r+\mbox{d}r)\mbox{d} S_{r}(\theta , \phi, r+\mbox{d}r) -A_{r}(\theta, \phi, r)\mbox{d} S_{r}(\theta, \phi, r)\\&= \left[A_{r}(\theta, \phi, r)+ \frac{\partial A_{r}(\theta, \phi, r) }{\partial r}\mbox{d}r \right] \left( \frac{1}{\mbox{d}r}\mbox{d}V +\frac{2}{r}\mbox{d}V \right) -A_{r}(\theta, \phi, r) \frac{1}{\mbox{d}r}\mbox{d}V \\&= \frac{\partial A_{r}(\theta, \phi, r) }{\partial r}\mbox{d}V +A_{r}(\theta, \phi, r)\frac{2}{r}\mbox{d} V\\&= \frac{1}{r^{2}}\frac{\partial \left[ r^{2}A_{r}(\theta, \phi, r) \right]}{\partial r}\mbox{d}V. \tag{15}](http://hooktail.maxwell.jp/bbslog/02a56e5b2f7fe5a67fb611db54d0f075.png)
式(13,14,15)を式(12)に代入して,ヴェクタ場の発散は;
![\mbox{div} \vec A(\theta,\phi,r) &:= \lim_{\mbox{d}V \to 0}\frac{\mbox{d}N_{\theta} +\mbox{d}N_{\phi} + \mbox{d}N_{r}}{\mbox{d}V} \\&= \frac{1}{r\sin(\theta)}\frac{\partial \left[ \sin(\theta)A_{\theta}(\theta, \phi, r) \right]}{\partial \theta}+\frac{1}{r\sin(\theta)}\frac{\partial A_{\phi}(\theta, \phi, r)}{\partial \phi} +\frac{1}{r^{2}}\frac{\partial \left[ r^{2}A_{r}(\theta, \phi, r) \right]}{\partial r} \tag{16}](http://hooktail.maxwell.jp/bbslog/3a38cb86b2fd66b253ac24856fb53545.png)
終わり.
■■■ごり押し計算をしてみて■■■
大学の電磁気をならって,初めての関門は「ヴェクトル場の発散」だろうと思います.逆に言えば,初めてぶつかる本格的な場の持つ幾何的な性質に遭遇しているわけです.
そんな大事な事態にいるのを,サラッと数学的な関係を計算できるようにするだけで過ごすのは,あまりにも物理の自主性に欠ける様に思います.
しかし,誰にも,こんな面倒な計算を求めるのも惨いと思います.それこそ,極座標での具体例を示し,どこら辺に,デカルト座標との違いが隠されているかを見てもらうのは,大変に教育的だと思います.
こう感じるのは,自分が数学の落ちこぼれだからだと思います.
でも,こうして計算してみると,勾配・回転なども似たように計算することができる事が「実体験を通して理解」できるようになります.今回の原稿を元に,幾何学的な計算法を纏めて見たいと思うようになりました.
今回の計算では,敢えて「?」を使いませんでしたが,自ずと外微分形式の算法が取り込めたと思います.というか,このようなナイーブな計算から外微分形式が生まれたのだろうとおもいます.
2007-05-04 zoro記. ■■■■■■■■■■■■■■■■■■■■■■■■■
■■■一寸おまけ■■■
スケイラ(スカラー)場, 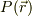 を考えて見ましょう.
を考えて見ましょう.
近接した2点間のポテンシャルの差分について,場の勾配を導入するのが素直かと思います.
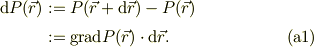
これに対して,極座標形式の位置の微分;
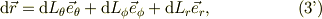
と,極座標表示でのポテンシャル
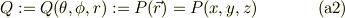
に注意すれば,極座標形式の勾配を出す事ができますね.
回転も手間ですが,計算できると推察しています(笑).
本当に終わり. ■■■■■■■■■■■■■■■■■■■■■■■■■ ■■■■■■■■■■■■■■■■■■■■■■■■■
Re: divについて
toorisugari no Hiro さんのレス (2007/05/03(Thu) 21:37)
>>よく読みましたが,正しく書いておられないし,「普通の微分と偏微分は間違え」というより「微分」そのもの,あるいはdiv,を理解されていないようにお見受します.
> 下のほうに訂正をしているということです. ::
> dE(x)/dtとなっていますが,偏微分のことです. > divE=(1/?x?y?z)(Eの面積分) (?x?y?z→0)=dEx/dt+dEy/dt+dEz/dt
これの事ですか?何故tが付いているのか相変わらず謎ですが,それならrot v(curl v)のz成分をこの記法でどう表すのでしょうか?
> あと,厳密性を気にするのはわかるのですが,そんなことでバカ扱いされるのは心外です.
バカにはしていません.理解されていないこと指摘した方が,tip★さんのためになると思っただけです.不愉快になられたのならお詫びします.
Re: divについて
tip★ さんのレス (2007/05/03(Thu) 21:52)
tはそれぞれx,y,zの間違えだなと汲み取ってくれれば,それでいいじゃないですか?多分みんな汲み取ってくれてますよ!
>>バカにはしていません.理解されていないこと指摘した方が,tip★さんのためになると思っただけです.
指摘の仕方が間違っていると思います.いきなり「理解してないのではないでしょうか?」というのはおかしいですよ.「tはそれぞれx,y,zの間違えではないでしょうか?」とか聞いて,そのあと,理解していないような返答があれば,「理解してないのではないでしょうか?」というべきです.
rot v・・・自分で言ってることとやってること矛盾してません?
vはベクトルとか,v=(v(x),v(y),v(z)) v(x)はvのx成分.ほかも同じ.とか 書くべきじゃないんですか?
これでは,あなたと同じになってしまいますので,汲み取って書かせていただきます.
(rot v)z={dv(y)/dx} - {dv(x)/dy}これは偏微分です.
Re: divについて
zoro さんのレス (2007/05/04(Fri) 22:02)
tip★さん,
こちらの数式掲示版の良い所は,簡易LaTeXが使えることです.
でも気分転換に,普通のテキストで書くときもあります.
>(rot v)z={dv(y)/dx} - {dv(x)/dy}これは偏微分です.
私だったら,次のように書きます;
(rot v)_z={∂v_y/∂x} - {∂v_x/∂y}.
・「_z」:下付きのz ・「∂」:偏微分記号
Re: divについて
佑弥 さんのレス (2007/05/04(Fri) 23:29)
たぶんtip★さんが習った発散の定義は,ガウスの発散定理
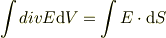
で左辺を微小体積の和に直して,極限をとった形
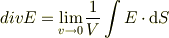
ではないですか?(僕の持ってる本でこの定義を使ってる本も結構 ありました.座標系によらない形という意味では便利かもしれません.)
tip★さんへ
汲み取ってくれるだろうという気持ちも分かりますが,それでも 戸惑ってしまいますよ.(tと見ると時間を思い浮かべてしまうこと にすっかり慣れてしまっていますから) 分かりやすくかけるところは分かりやすく書いていただけると, 返信する側としても読みやすいです.
と言いつつ,上式でベクトルの太字が打てなかったので,説得力が あまりないですが・・・
ちなみに,普通に分を打つ時は,TeXを使わない場合デルと打てば∂が 打てます.
Re: divについて
tip★ さんのレス (2007/05/05(Sat) 00:30)
>>zoroさん
これを期にTexのやり方を学びたいのですが,何からはじめたらいいですか? 今使っているパソコンは自分のではないので,ソフトとかは入れられないのですが,何かいい方法があったら教えてください.
>>佑弥さn すみません.ついあつくなってしまいました.
Re: divについて
zoro さんのレス (2007/05/05(Sat) 04:12)
tip★さん,
>これを期にTexのやり方を学びたいのですが,何からはじめたらいいですか?
とても良い着眼点だと思います.
>今使っているパソコンは自分のではないので,ソフトとかは入れられないのですが,
でも,ご心配無用です.現在,この掲示板にアクセスできる人は皆さん,この掲示板を使う限り,数式を書けますから.そして,ここには,練習用の「数式掲示板」もあります.
>何かいい方法があったら教えてください.
一番有効で,簡単なのは,以下に示すように,論議相手の表現を「まねっこ」する事です.
あと,お勧めは,LaTeXの解説書を1冊,手元に置かれると良いでしょう.例えば;
LaTeX2e 美文書作成入門 奥村 晴彦・著 技術評論社 ISBN4-7741-1940-7
など.もし,ご推奨の本があれば,お教え下されば幸いです.→皆様.
さて,本論です.
「toorisugari no Hiroさんの記事:2007/05/02(Wed) 19:18 No.15604」をコピーしてきます.
- 〜〜〜〜〜〜コピー&ペースト:はじめ〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜
- つまり,こういう問題なのですね.
「 1. bm{E}=E_xbm{e}_x+E_ybm{e}_y+E_zbm{e}_zとしてtext{div}bm{E}=partial_x E_x + partial_y E_y +partial_z E_z を示せ.(ただし,partial_x=frac{partial}{partial x}.bm{e}_iはi方向の単位ベクトル.) 2. text{div}bm{E}の極座標表示をもとめよ. 」
じゃ,先に聞いた bm{r}=left( begin{array}{c} r sintheta cosphi\ r sintheta sinphi\ r costheta end{array}right) としたとき, mathrm{d}bm{r}=h_r mathrm{d}r bm{e}_r + h_theta mathrm{d}theta bm{e}_theta + h_phi mathrm{d}phi bm{e}_phi となるのはできますか?これがわかれば,それぞれの微小ベクトル(h_ideltapsi_ibm{e}_i)が張る直方体で考えればよいです. 〜〜〜〜〜〜コピー&ペースト:おわり〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜
以上を「まねっこ」する方法を示します.
●●●1文章中での数式●●●
対象:
「 2. text{div}bm{E}の極座標表示をもとめよ. 」
数式の部分は「text{div}bm{E}」が文章中に埋め込まれています.これをLaTeX表現にするには,前後に<Tex>と</Tex>をつけ;
「 2. <Tex>text{div}bm{E}</Tex>の極座標表示をもとめよ. 」
「T」→「t」にしますと,
「
2. 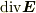 の極座標表示をもとめよ.
」
の極座標表示をもとめよ.
」
となります.
同様に,このように複雑な例でも;
「 1. bm{E}=E_xbm{e}_x+E_ybm{e}_y+E_zbm{e}_zとしてtext{div}bm{E}=partial_x E_x + partial_y E_y +partial_z E_z を示せ.(ただし,partial_x=frac{partial}{partial x}.bm{e}_iはi方向の単位ベクトル.) 」
それぞれの数式部の前後を<Tex>..</Tex>で包んで,
「 1. <Tex>bm{E}=E_xbm{e}_x+E_ybm{e}_y+E_zbm{e}_z</Tex>として<Tex>text{div}bm{E}=partial_x E_x + partial_y E_y +partial_z E_z</Tex> を示せ.(ただし,<Tex>partial_x=frac{partial}{partial x}</Tex>.<Tex>bm{e}_i</Tex>はi方向の単位ベクトル.) 」
「T」→「t」にしますと,式が表示される筈ですね.例題として,上をコピーして,テスト用の掲示板;
にペーストした上で,「T」→「t」すれば,その効果を見る事ができます.
●●●2独立した数式(別行立ての数式)●●●
例:
「 じゃ,先に聞いた bm{r}=left( begin{array}{c} r sintheta cosphi\ r sintheta sinphi\ r costheta end{array}right) としたとき, 」
この場合,<Tex>と</Tex>との間にリターンを一個以上いれます.私は,次のようにしています;
「 じゃ,先に聞いた <Tex> bm{r}=left( begin{array}{c} r sintheta cosphi\ r sintheta sinphi\ r costheta end{array}right) </Tex> としたとき, 」
「T」→「t」にしますと,
「 じゃ,先に聞いた
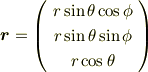
としたとき, 」
となります.列ヴェクタ表示のコマンドの為に,式が複雑ですが,参考書に説明は在るので,「まねっこ」する毎に確認して行けば,すぐにマスタできるとおもいます.
●●●3物理での数式表現●●●
物理だけでなく数学でもそうだと思いますが,「数式」はとても表現力が在るものです.
でも,本当に重要なのは,検討している対象のもつ「物理的な解釈」なり「数学的な解釈」だと思います.くれぐれも「数式」に振り回される事のないようにして下さい.
とは言え,LaTeXになれると,自分の考えを熟成するのがとても効率よくなります.
Re: divについて
zoro さんのレス (2007/05/05(Sat) 05:04)
佑弥さん,
〜〜〜〜引用:初め〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜 極限をとった形
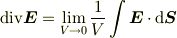
ではないですか?(僕の持ってる本でこの定義を使ってる本も結構 ありました.座標系によらない形という意味では便利かもしれません.) 〜〜〜〜引用:終り〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜
というのは面白い考え方だと思います.
自分の感触としては,もう少し詳しく書く;
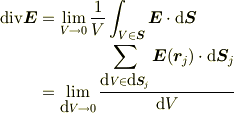
とかの工夫が欲しいとおもいます.しかし,通常は微分形式から習い始める訳で,そこに積分形式が出て来ると判り難くなると感じます.
でも,初学者に「積分形式から始まって,微分形式に至る」ような解説も在り得るようにも感じてきました.是非ともトライされると良いですね.
また,「座標系によらない形」という視点を取り入れた解説も素敵だとおもいます.是非とも新たな観点の展開が望まれます.
Re: divについて
佑弥 さんのレス (2007/05/05(Sat) 10:21)
zoroさんへ
僕もこの定義は面白いと思いました.この式のほうが 直感的にも湧き出す感じが出てる気がします.(ただ, 厳密にこの式が成立するのかを証明したことがないので, 便利な式ぐらいの認識しか持ってないですが・・・) 暇な時にでも証明を考えて見たいと思ってます.
大学の授業がそこまでいってないので,実際どのように 習うのかは分からないですが,本ではこの式から通常の 公式も導いてました. でも,確かに数学の本では微分から定義するのが普通み たいですね.
Re: divについて
toorisugari no Hiro さんのレス (2007/05/05(Sat) 16:14)
の定義
「 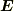 は(面密度)ベクトル場である.
は(面密度)ベクトル場である. 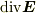 は
は
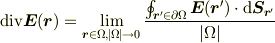
を満たす(体積密度)スカラー場である.
ただし, 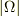 は領域
は領域 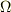 の体積,
の体積, 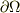 は領域
は領域 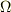 の境界である.
」
は最近のまっとうな教科書なら必ず載っています.(再定義という形を取ることもありますが.なお,上の定義は冗長に書きました.)これはイメージ的に理解しやすい形ですし,
の境界である.
」
は最近のまっとうな教科書なら必ず載っています.(再定義という形を取ることもありますが.なお,上の定義は冗長に書きました.)これはイメージ的に理解しやすい形ですし,
これを定義とするならばガウスの定理の本質部分は
「
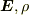 は領域
は領域 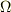 をふくむ領域で定義された(面密度)ベクトル場,(体積密度)スカラー場である.領域
をふくむ領域で定義された(面密度)ベクトル場,(体積密度)スカラー場である.領域 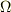 がふたつの領域
がふたつの領域 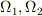 に分割されるなら,
に分割されるなら,
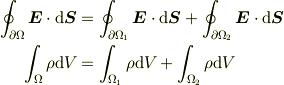
が成り立つ. 」 という「足し算則」になってしまうので,非常に理解しやすいですね.
なおzoroさんがおっしゃるように近似式までおとすべきかもしれませんが,そうすると座標系に依存しないという部分が消えてしまいます.
計算するときに適切な格子を設定して解くとした方が汎用的です.(この計算が,本質的にはガウスの定理の従来の証明に相当する部分です.)
Re: divについて
tip★ さんのレス (2007/05/05(Sat) 18:07)
ここの人は,みんなかなりレベルが高いですね・・・ちょっとついていけない部分があります.
こんなに自分の未熟さを思い知ったのは初めてです.一応大学ではできているほうなんですが・・・あっ!国公立ですが,旧帝大ほどレベルが高いわけではありませよ!
大学1年で習った電磁気学は何だったんだって感じです・・・厳密性にかけるというか何というか・・・時間の関係もあるんでしょうが・・・
そこでなんですけど,電磁気学をもう一度やり直したいと思っています. みなさんが2冊目に読んだ電磁気学の本なんでしょうか?ある程度難しめで,ある程度厳密性のある本が知りたいのですが,何かないでしょうか?
Re: divについて
toorisugari no Hiro さんのレス (2007/05/05(Sat) 19:37)
> みなさんが2冊目に読んだ電磁気学の本なんでしょうか?ある程度難しめで,ある程度厳密性のある本が知りたいのですが,何かないでしょうか?
2冊目というわけではないですが,このサイトで評判になっているのは 「マクスウェル方程式・電磁気のよりよい理解のために」北野正雄(数理科学臨時別冊SGCライブラリ39) です.ただし,4回生以上でないと難しいと思います.
- http://www.moge.org/okabe/temp/elemag/temp.html
- http://edmain.ed.kyushu-u.ac.jp/~hayashi/lecturenote.pdf
あたりから勉強されることをおすすめします.
Re: divについて
tip★ さんのレス (2007/05/05(Sat) 19:50)
ありがとうございます
Re: divについて
zoro さんのレス (2007/05/05(Sat) 22:02)
私の場合,反面教師としての事例として書いて見ます.
(1)The Feynman Lectures on Physics (World Student) (ペーパーバック) Richard Phillips Feynman , Robert B. Leighton , Matthew Sands・共著
電磁気の巻だけは,新刊のハードカバーで,1年の夏休みまでは勉強した. 夏休み後,友人達に,それで計算が出来るようになったの?,といわれギャフン.
(2)ベクトル解析,安達 忠次・著,培風館 (1961/09)
(1)の反省を踏まえ,数人の友人と,勉強会をしてベクトル解析を操れるようになったものの,物理的な解釈が出来ず,ファインマンさんの本とのギャップが埋まらなかった.
(3)理論電磁気学 初版,砂川 重信・著,紀伊国屋書店
当時は,とても感激して読みました.でも行き過ぎて他の分野まで,この本から解釈するようになりました.
この本は,ある意味で,わが国の宝と言っていいでしょう.しかし,より現代的な電磁気学の本が望まれるとも思います.これに付いては現役の方々のご意見をお聞きくださるとよいですね.
〜〜〜〜 (4)電磁気学の考え方,砂川 重信・著,岩波書店
こちらのサイトに来るようになり,手元に本が無かったので買ってみた.自分には(3)の印象が強すぎて,この本にはなにか違和感があります.きっと,初心者の方にも好みが分かれるかもしれません.ご自分の目で確認される事をお勧めします.
このp131に,「さらに勉強したい人のために」を参考にされるのもよいでしょう.
ただ,同著者による「物理の考え方シリーズ 全5巻」なので,辞書代わりにして見るといった勉強用の書として面白いかもしれません.
Re: divについて
zoro さんのレス (2007/05/05(Sat) 23:34)
toorisugari no Hiroさん,
>は最近のまっとうな教科書なら必ず載っています.(再定義という形を取ることもありますが.なお,上の定義は冗長に書きました.)これはイメージ的に理解しやすい形ですし,
このご発言を見落としていました.ご存知の教科書をなるべく完全にお教え下さいませんか.
また,その様な本ですと,回転の論議も類似の方法で解説しているとは思いますが,もし上記の本以外があれば,それもお教え下さいませんか.
なお,これらの教科書は,日本語・英語に限る事にします.以上,お手数ではあると思いますが,宜しくお願い申し上げます.
Re: divについて
zoro さんのレス (2007/05/06(Sun) 09:02)
toorisugari no Hiroさん,
昨晩にお願いした教科書についてのお願いは取り下げさせて頂きます.
昨日は幾つかの話が並行的に進み,睡眠不足の中で,こちらのスレッドもよく読めないで勝手に混乱していました.
今日よく寝て見ると,各所で支離滅裂の論議をしていて恥じています.上のお願いもその一つでした.
今回,極座標で,「 grad」,「div」と来たのだから,「rot」でも似たような論議をすれば良さそうだが,どうだろうかと思い質問してしまったのです.
冷静になれば,「積分形式の式で,その積分範囲を微小領域に押し戻せば微分形になる」という精神に従えばよい事に気づきまして, 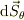 の微小面積素について予備計算をしてみると,確かに
の微小面積素について予備計算をしてみると,確かに 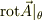 が計算できているようです.
が計算できているようです.
このように具体的な「ごり押し計算」をしているうちに,「grad」,「div」,「rot」の定義にはヴェクタの内積という形が共通に出てきていると思い至りました.こういう肝心な点を今頃気づくというのが,素人の怖さでしょうね.
おそらく,佑弥さんが書かれた
>(僕の持ってる本でこの定義を使ってる本も結構ありました. >座標系によらない形という意味では便利かもしれません.)
とも関係しそうです.私としては,極座標という具体的な計算過程をもうすこし眺める事で,何かを感じられそうだと思います.
#rotの導出は,昨年 Johさんが解説記事をかかれたと思います. #当時は生半可に面白く感じましたが,漸くあの解説の本当の面白さを実感しています.
今度は,自分でも考えて見たいと思います.
>(面密度)ベクトル場,(体積密度)スカラー場
というのも,おぼろげに判るような気がしてきました.敢えて「回転はなんていうの」という質問はホールドしておきます(笑).
Re: divについて
toorisugari no Hiro さんのレス (2007/05/07(Mon) 13:40)
> 敢えて「回転はなんていうの」という質問はホールドしておきます(笑).
あえて体積で定義してみましょうか.
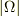 は領域
は領域 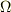 の体積,
の体積, 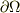 は領域
は領域 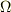 の境界とする.
の境界とする.
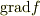 の定義
「(点)スカラー場
の定義
「(点)スカラー場  に対して,
に対して,
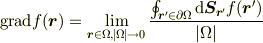
を満たす(線密度)ベクトル場 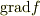 を勾配という.
」
を勾配という.
」
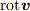 の定義
「(線密度)ベクトル場
の定義
「(線密度)ベクトル場 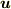 に対して,
に対して,
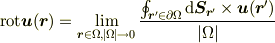
を満たす(面密度)ベクトル場 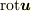 を回転という.
」
を回転という.
」
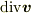 の定義
「(面密度)ベクトル場
の定義
「(面密度)ベクトル場  に対して,
に対して,
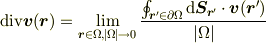
を満たす(体積密度)スカラー場 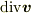 を発散という.
」
を発散という.
」
これらはガウスの定理を変形したもの
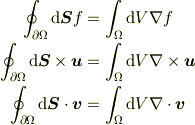
からでてきます.証明は左辺に定ベクトル 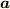 を内積でかけて,通常のガウスの定理と公式
を内積でかけて,通常のガウスの定理と公式
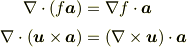
を使えば証明できます.使われている例として
を挙げておきます.
左辺がそのまま微分形になっているし,幾何学的にもイメージしやすいのですが,反面,座標変換の計算はかえって面倒です.^^;
計算のためなら普通に
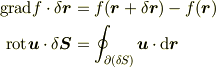
がいいでしょうね.
Re: divについて
zoro さんのレス (2007/05/07(Mon) 16:57)
>あえて体積で定義してみましょうか
なるほど,勾配や回転をヴェクタとして直に定義するのは面白いです.でも,直感に裏打ちされた説明でないと,物理系の初心者,とくに私のように頑固で,数学が苦手な者には著しく抵抗が高いと思います.
しかし,約1年に渡り,物理数学の周辺を見直し,今回の極座標での発散を完全に書き下し,一部回転も計算した現在の視点では,上記のような「gradやrotなどのヴェクタ演算子を直接定義する方法」が心に響きます.当面,折に触れて考えてみようと思います.
ご紹介のサイトは,近くのスレッドで「SI単位系」の論議の時に,拝見しました.物理教育に於けるインターネットと活用の一法を示されていて,更に内容が充実していると思います.自分も,一部だけでも「自分で作った解釈」を書いて行ければいいな,と思います.
極座標での計算は,tip★さんが,予習か復習かを兼ねて書いて下さると素敵だとおもいます.勿論; >計算のためなら普通に で,結構ですよ.
これにて,お爺さんの出番は終わりにします.
Re: divについて
zoro さんのレス (2007/05/28(Mon) 10:25)
労作を拝見させて戴きました.この事は,何十年先にも思い出せる事を保証します(笑).
ちょっと,細かい所をコメントします.
- 左辺の面積分:
私もかっては,面積分で,2次元だから積分記号も二重にしていました.でも,toorisugari no Hiroさんに「面積という一つのパラメータの積分だから,積分記号は一つ」と教えられました.以来,私は,その定義に従っています.
ところが, 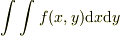 では,2つのパラメータの積分なので,積分記号も2ついると考えるようです.
では,2つのパラメータの積分なので,積分記号も2ついると考えるようです.
#勿論,数学的な記号は,自分の好きに使っていいので,自分のノートでは,変梃な記号が跋扈しています. #上の積分の例でも,自分のノートでは,
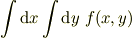
ですし, 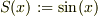 です.
外に出す時は,勿論修正します.
です.
外に出す時は,勿論修正します.
- 右辺の第一項
左辺の積分で,Sが微小である事から,積分を内積の和にしたのだと思いますが,法線ベクトルが,それぞれどこを向いているかの表示が欲しいように思います.例えば,( 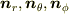 )とか.
)とか.
- >図とかなくて分かりにくいと思いますが,自分ではこれが限界です.
LaTeXは数式を文によって書き出すことを可能にしてくれた訳ですよね.同じように,説明図を文によって書き出してくれる簡単な方法が欲しいと思います....
とにかく,紙のノートでも,PCでのノートでも,書いてみない事には巧くならないので,ガンガンと書いて下さいね.
Re: divについて
toorisugari no Hiro さんのレス (2007/05/28(Mon) 14:25)
tip★さん,ご苦労様です.
いくつかはzoroさんが指摘されましたが,一つだけ.
図形の中心を 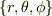 にされた方が式は最終的にきれいになります.
にされた方が式は最終的にきれいになります.
これは微分 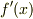 を
を 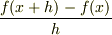 (前進差分)で近似するのでなく,
(前進差分)で近似するのでなく, 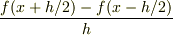 (中心差分)で近似することに相当します.
(中心差分)で近似することに相当します.
************************************
なお,divは他にも求め方があります.
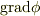 の表現がわかっているとします.(ここで,
の表現がわかっているとします.(ここで,  は無限遠で速やかに0になる任意関数とします.)
公式
は無限遠で速やかに0になる任意関数とします.)
公式
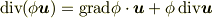
を全空間で体積積分してガウスの定理を使うと(  が無限遠で消えるから),
が無限遠で消えるから),
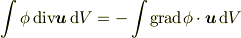
この式の右辺に具体的な表現( 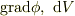 )をいれて部分積分をすると
)をいれて部分積分をすると 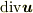 の具体的な表現が得られます(面積を考慮しなくて良い分楽だと思います).
時間に余裕があれば試してみてください.
の具体的な表現が得られます(面積を考慮しなくて良い分楽だと思います).
時間に余裕があれば試してみてください.
Re: divについて
zoro さんのレス (2007/05/30(Wed) 18:33)
こういうのは,「趣味的な勉強」の側面があります.正規な勉強で,時間が余った時に日常的な常識からすこしエスケイプして「ああだ,こうだ」と自分の感覚の示す方向を探索する事だと思います.
勉強すれば,するほど,疑問点はでてくるので,その中でも「特に大きな疑問」を対象に趣味的な探索をされると面白いですね.
そして,その結果が正しそうだったら,色々な機会(この数式掲示板もその一つ)にそれを書いて,他の人に説明すると,とても力が付くように思います.こんなに面白い事を,教師・教官の方々に独占させて置くのは,もったいない事だと思います.