熱伝導について

まささんの書込 (2007/04/30(Mon) 04:17)

こんにちは．大学学部3年ですが，熱伝導の問題で躓いておりますのでご助力をお願いいたします．

厚さ ,熱伝導率の平板をマイクロ波で加熱する．この時，単位体積，単位時間あたり以下の熱量が生じるとする．

$H(x)=H_0\left(1-\frac{x}{L}\right)\mathrm{[W/m^3]}\quad H_0=\mathrm{const}$

ここで, |d41d8cd98f00b204e9800998ecf8427e|x|d41d8cd98f00b204e9800998ecf8427e| はマイクロ波の入射する表面から内部への距離である．

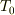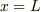物体の表面は温度 T_0 の気体に熱伝達率 $\alpha$ で伝熱し，平板は x=L で断熱されているとする．

定常状態として，温度分布を求めよ．

と言う問題です．

以下は自分で考えた解答です．この場合の定常1次元熱伝導方程式は

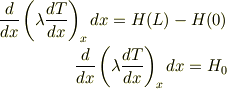
$\frac{d}{dx}\left(\lambda\frac{dT}{dx}\right)_xdx=H(L)-H(0)\\\frac{d}{dx}\left(\lambda\frac{dT}{dx}\right)_xdx=H_0$

よって平板内の温度分布の一般解は

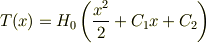
$T(x)=H_0\left(\frac{x^2}{2}+C_1x+C_2\right)$

上もかなり不安ですが,ここからが更に分かりません．境界条件

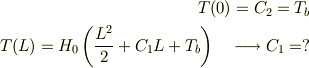
$T(0)=C_2=T_b\\T(L)=H_0\left(\frac{L^2}{2}+C_1L+T_b\right)\quad \longrightarrow C_1=?$

となり,どのように境界条件を求めたらよいのでしょうか．ご助力の程お願いいたします．

すこし考え方だけ書いてみます．間違っているかもしれませんが．

求めるべき温度は，時間的に変動のないものとします：温度T(x).

熱エネルギ流Jは単位面積あたりに，単位時間内の量として，J(x) = -kdT/dx.(1)

いま物体の内部で，面積S，位置(x, Δx)の部分で，時間幅Δtでのエネルギ収支は，時間的に定常だから；

０ = J(x)SΔt +H(x)SΔxΔt -J(x+Δx))SΔt,

故に dJ/dx = H(x).(2)

両端での熱エネルギ流の境界条件；

[a] x=0で； -α{T(0) -T_0}SΔt = J(0)SΔt←加熱された分は，(J < 0)となり表面にむかい，熱伝達率によって，気体に奪われるから．

[b] x=L で；０ = J(L)SΔt←断熱面に接しているので，エネルギを放出できない．

従って J(L) = 0.(4)

以上を(1)〜(4)連立して求めるような気がしましす．符号などは，間違えているかもしれませんから，ご確認のほどを．特に(3)の使い方は初めてなので，自信がありません．