原子モデルについて

原子モデルについて

早弥 さんの書込 (2007/04/28(Sat) 23:53)

こんばんはー．最近量子力学について勉強し始めたんですけれど，質問していいですか？ ボーアの原子モデルで残った問題をシュレーディンガーの方程式は説明したんですよね？ボーアの原子モデルとシュレーディンガーの方程式によって導かれた原子モデルの違いっていうのは，ボーアの原子モデルでは，とびとびに存在する天体型の軌道を電子がまわっているしているのに対して，シュレーディンガーの方程式から導かれるのは，電子はその存在領域が確立分布によってしか決まらないってことでよいのでしょうか？

Re: 原子モデルについて

zoro さんのレス (2007/04/30(Mon) 02:34)

早弥さん，初めまして．

大雑把に言えば，ボーア模型では「とびとびのエネルギ順位を出す事はできて，順位間のエネルギ差として水素のスペクトルを出せるようになった」事が凄かったのだろうと思います．

ところが，輝線スペクトルの強度比，順位間の遷移規則など，定量的な予測に手も足も出なかったので，「新たなダイナミックな量子モデル」の探求が行われたのだとおもいます．

その一つとして，シュレディンガーさんの波動力学と，ハイゼンベルグさんの行列力学が出て来たのだと思います．両者は，一見すると違うようですが，数学的には同等であることが判明し，イメージしやすい波動力学が主流になったと思います．

私の私見ですが，この両者の良いとこ取りをしたのが，ディラックさんのブラ・ケット表示だとおもいます．

Re: 原子モデルについて

toorisugari no Hiro さんのレス (2007/05/01(Tue) 14:51)

スレ主さんの質問には関係ない話ですが，

> その一つとして，シュレディンガーさんの波動力学と，ハイゼンベルグさんの行列力学が出て来たのだと思います．両者は，一見すると違うようですが，数学的には同等であることが判明し，イメージしやすい波動力学が主流になったと思います．

最後の文は疑問ですが，まあ問題ないとしますが，

> この両者の良いとこ取りをしたのが，ディラックさんのブラ・ケット表示だとおもいます．

でたらめです．ディラックが両描像の等価性を示したのは事実ですが，ブラ・ケット表示とは直接の関係はありません．

ブラ・ケット表示は，単に，双対ベクトルをわかりやすく便利に使うための表示方法にすぎません．

Re: 原子モデルについて

zoro さんのレス (2007/05/01(Tue) 15:19)

＞でたらめです．ディラックが両描像の等価性を示したのは事実ですが，ブラ・ケット表示とは直接の関係はありません． ＞ブラ・ケット表示は，単に，双対ベクトルをわかりやすく便利に使うための表示方法にすぎません．

記憶だけで書いているので，根拠は示せません．しかし「双対ベクトルをわかりやすく便利に使うための表示方法」とまで言い切れるとは驚きです．出典をお教え下されば，将来勉強したいと思います．

＞最後の文は疑問ですが，まあ問題ないとしますが，

疑問点があるなら，対立意見をお書きにならないと訳が判りませんね．色々な角度からの論議がでて，そのなかからより正しそうな解釈に進む事ができると思います．

Re: 原子モデルについて

toorisugari no Hiro さんのレス (2007/05/01(Tue) 17:19)

> 出典をお教え下されば，将来勉強したいと思います．

Dirac 「量子力学」朝永他 訳 24ページ 「§6ブラベクトルとケットベクトル どんな数学理論においても，一組のベクトルがあるときにはいつでも必ずもう一つ別の組のベクトルを作り上げることができるが，これを数学者はdual vectorと呼んでいる．dual vectorを作る手続きを，元のベクトルがいま考えているケットベクトルである場合について述べる．(以下略)」

> 疑問点があるなら，対立意見をお書きにならないと訳が判りませんね．

「初心者向けにはシュレンディンガー表示が使われることが多い」という意味と，好意的に解釈したまでです．

> 波動力学が主流になったと思います．

ハイゼンベルグ描像もよく使われています． (というか，どちらの描像も演算子とベクトルで記述できるということを示し，時間発展演算子をどちらに作用させるかが，ふたつの表示法の差異であると喝破したのがDiracです．中間的な相互作用描像という考え方もあります．場の理論までいくと演算子を中心にした考え方が主流であるという意味では，むしろハイゼンベルグ流(演算子法)が主流といえなくもないです．)

Re: 原子モデルについて

zoro さんのレス (2007/05/01(Tue) 17:41)

＞Dirac 「量子力学」朝永他 訳 ＞24ページ ＞「§6ブラベクトルとケットベクトル ＞どんな数学理論においても，一組のベクトルがあるときにはいつでも必ずもう一つ別の組のベクトルを作り上げることができるが，これを数学者はdual vectorと呼んでいる．dual vectorを作る手続きを，元のベクトルがいま考えているケットベクトルである場合について述べる．(以下略)」

双対性について正確に理解していませんが，上の記述は，ある1組の完全直交系があったら，それを線形変換してたの別の1組の完全直交系に変換する事ができるとくことではありませんか？ 同じ事は，波動関数でもできるのであって，双対性とブラ・ケット表示とが本質的な関係をもつのですか？

私は，ディラックさんの量子力学は理解できなかったのですが，一度は読んでみたいと思い出しています．

＞ハイゼンベルグ描像もよく使われています． ＞(というか，どちらの描像も演算子とベクトルで記述できるということを示し，時間発展演算子をどちらに作用させるかが，ふたつの表示法の差異であると喝破したのがDiracです．中間的な相互作用描像という考え方もあります．

自分の関係した分野では，時間依存のある量子力学を必要としなかったので，なるほどな，と思います．ここら辺も含めて，ディラックさんに挑戦したいと思います．

＞場の理論までいくと演算子を中心にした考え方が主流であるという意味では，むしろハイゼンベルグ流(演算子法)が主流といえなくもないです．)

ここまで含めてお書きになっているとは，思いもしませんでした．最初の質問を考えると，唐突な感じを持ちます．ある問題や疑問にアタックするときには，一挙に問題点を羅列して，正面突破をする事もあるでしょう．しかし，この掲示版では，そのようなプロフェッショナルな方法論は誤解を生む危険性が高いと思います．

また，数学的手法等にお詳しいのは，よく判りますが，あくまで物理的解釈を明確にするための一法であるように思います．まあ，余談ですが ...．

Re: 原子モデルについて

toorisugari no Hiro さんのレス (2007/05/01(Tue) 21:42)

> 上の記述は，ある1組の完全直交系があったら，それを線形変換してたの別の1組の完全直交系に変換する事ができるとくことではありませんか？

引用した部分が短いので，そうともとれますが，違います．ベクトルからスカラーへの線形関数を定義し，その関数に対応する「ベクトル」をブラと定義しています．スカラー積を頭に入れて考えればブラが双対ベクトルであることは自明だと思いますが．．．

# dual vectorを調べられましたか?

Re: 原子モデルについて

zoro さんのレス (2007/05/01(Tue) 22:58)

＞引用した部分が短いので，そうともとれますが，違います．ベクトルからスカラーへの線形関数を定義し，その関数に対応する「ベクトル」をブラと定義しています．スカラー積を頭に入れて考えればブラが双対ベクトルであることは自明だと思いますが．．．

今のレベルの自分では，「自明」とは程遠い状態です．恐らく，学部の前期課程での量子力学を終えた方でもそうではないでしょうか．

推定ですが，そのような対応物は，普通の波動方程式でも類似の論議は成り立つのだろうと思います．自分は現在のところ，古典的な力学・電磁気学をほぼ思い出し，特殊相対性理論を復習中です．すこし前衛的なヴェクタ解析を学びたいですが，数学色の薄い本がなく，偶然に岩波の「理工系の基礎数学 Vol.10 微分・位相幾何」を知り，手を出し始めたところです．というわけで，量子力学の再勉強は，数年先になりそうです．

でも，なんのかんの言っても，ディラックさんの本がいまもって多くの読者を引き付けているのを拝見し，例えば，アクティヴなクロメルさんの本棚；

にもあり，私も再挑戦してみたいと思っていました．

# dual vectorを調べられましたか?

上に述べたように，まだ調べる段階ではありませんが，ご紹介の後者には，それほど違和感無く拝見できました．

先にお示しした「微分・位相幾何」でも，p9に双対空間がチラと出ますが，その後， p212のコホモロジー群の「双対性」までは影を潜めているようです．

まあ，頭の硬い私が，どれ程，この本を理解できるか判りません．当面，量子力学分野での伸展は望むべくもないと思われます．

とんだところで「双対性」の関連を教えていただき有難うございました．

〜〜〜〜 早弥さん，

私の書き込みが不十分な為に，とんでもない話に発展して申し訳ありませんでした．

これに懲りずに，「不思議だな」と感じた点を質問されると宜しいかと思います．

Re: 原子モデルについて

toorisugari no Hiro さんのレス (2007/05/01(Tue) 23:14)

> 恐らく，学部の前期課程での量子力学を終えた方でもそうではないでしょうか．

そうです．だからこそ，双対空間という簡単な割にはイメージしづらい概念をブラとケットという表示で表現したDiracは偉いわけですね． # もちろん縦「成分表示」と横「成分表示」でも同じですが，美しさが．．．．

> そのような対応物は，普通の波動方程式でも類似の論議は成り立つのだろうと思います．

はい．

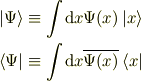
\left|\Psi\right\rangle &\equiv \int\mathrm{d}x \Psi(x)\left|x\right\rangle\\\left\langle\Psi\right| &\equiv \int\mathrm{d}x \overline{\Psi(x)}\left\langle x\right|
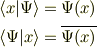
\left\langle x|\Psi\right\rangle &= \Psi(x)\\\left\langle\Psi|x\right\rangle &= \overline{\Psi(x)}

完全性をつかえば

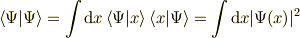
\left\langle\Psi|\Psi\right\rangle &=\int\mathrm{d}x \left\langle\Psi|x\right\rangle \left\langle x|\Psi\right\rangle = \int\mathrm{d}x |\Psi(x)|^2

ただし 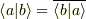\left\langle a|b\right\rangle = \overline{\left\langle b|a\right\rangle} です．(複素ベクトル空間)

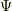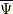つまり，波動関数は状態ベクトルの，位置(演算子の固有)ベクトルを基底としたときの，成分表示にすぎません．そして \Psi の双対は \overline{\Psi} だと思っても良いです．(成分の話なので無理があるのは承知．)

Re: 原子モデルについて

zoro さんのレス (2007/05/02(Wed) 09:54)

早弥さん，

中途半端な記憶に基づいて書き込みをして，すいませんでした．

toorisugari no Hiroさんのような現役の方の解説により，量子力学のもつ「数学的な一面」に触れる事が出来て，私も，もう少しべんきょうしたいな，と思いました．

＃それにしても，ディラックさんの頭の中を見る事ができたら，面白いでしょうね．

きっと，早弥さんが後期課程の量子力学を取られる頃に，私も，そのレベルの勉強すると思われます．その頃には，もう少しましな論議が出来るようになれたら嬉しいです(笑)．

Re: 原子モデルについて

早弥 さんのレス (2007/05/06(Sun) 23:37)

ありがとうございました． 量子力学って奥が深いんですね！お二人の議論を読んでて実際頭くらくらしますけど(笑)がんばって勉強したいと思います．