グラディエントとは

みちるさんさんの書込 (2007/04/26(Thu) 18:36)

電磁気学を通じてそれなりに分かったつもりの「勾配grad」ですが，最近悩むようになりました．というのも，偏微分の授業を今受けているのですが，その授業で突然「gradは法線ベクトルを表す」と言われました．私の感覚だと，例えば電気のポテンシャルに対してgradを取れば電場を示すように，勾配という文字の通り，接線のベクトルを表すものなのですが．ただこちらのサイトのベクトル解析のページにも「∇φは法線ベクトルになる」と掲載されています．私が今のところ予想しているのは， ?y=ax+bなどの陽関数なら，微分して接線の方向を示すけれど ?f(x,y)=ax+by+cなどの陰関数なら，偏微分して法線の方向を示すといった感じなのですが…イマイチつかめませんし，（すごく）間違っている気もします．

どなたか，ご教授お願いいたします．

P.S. 最近テンソルとやらも出てきて，数学ばっかり詰まるようになりました．またしばらくお世話になるかもしれません．

Re: グラディエントとは

toorisugari no Hiro さんのレス (2007/04/26(Thu) 18:55)

地図を眺めて，等高線と傾きが一番大きい方向の関係を調べてください．

傾きベクトルは「その地点で傾きが一番大きくなるような方向(+向き)，その方向に進んだ時の傾きを大きさ」とするベクトルです．

なお，地図における傾きベクトルは2次元平面(水平面)内のベクトルであることに注意してください．

Re: グラディエントとは

yama さんのレス (2007/04/26(Thu) 22:38)

電場のポテンシャルの勾配は，電気力線の接線ベクトルであると同時に等電位面の法線ベクトルでもあります．単に接線とか法線とかではなく，何の接線か，何の法線かを理解しておくことが大切です．

Re: グラディエントとは

みちるさんさんのレス (2007/04/28(Sat) 01:58)

＞toorisugari no Hiroさんその意味では，「接線方向」ですよね．

＞yamaさんえっ…

電気量をＱとすると，そこからｒの位置における電位ポテンシャルは V=kQ/rと書けるのに対し，電場の大きさは E=kQ/r^2と書けますよね．ポテンシャルを位置で微分すれば，とりあえずマイナスはおいといて，電場になりますよね．

これはすなわち等電位面の微分が電場を意味することから，接線方向となるのではないでしょうか？

もっと単純に考えて，「電位の山があるときに，ボールが下っていく向きが電場」というイメージではないでしょうか．長年この感覚で生きてきたのですが．

Re: グラディエントとは

zoro さんのレス (2007/04/28(Sat) 04:30)

横から失礼します．

＞電気量をＱとすると，そこからｒの位置における電位ポテンシャルは＞V=kQ/rと書けるのに対し，電場の大きさは

せっかくここまで来たのですから，スカラー(スケイラ)で止めないで，ベクトル(ヴェクタ)として計算してみませんか．とくに球対称での計算を，デカルト座標から計算するのは，指の練習にも好適で，イザ公式を忘れた時にも有用です．

さて，

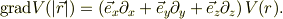
$\mbox{grad} V(|\vec r|) =\left( \vec e_{x} \partial_{x} + \vec e_{y} \partial_{y} + \vec e_{z} \partial_{z} \right) V(r).$

ここで，ポテンシャルは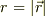， $r=|\vec r|$ の関数で，球対称関数である事に注意します．

ピタゴラスの関係で，

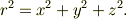
$r^{2} = x^{2} +y^{2} + z^{2}.$

陰関数の偏微分の関係式,たとえばxについては，

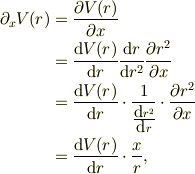
$\partial_{x}V(r) &= \frac{\partial V(r)}{\partial x}\\&= \frac{\mbox{d} V(r)}{\mbox{d} r}\frac{\mbox{d} r}{\mbox{d} r^{2}}\frac{\partial r^{2}}{\partial x}\\&= \frac{\mbox{d} V(r)}{\mbox{d} r} \cdot \frac{1}{\frac{\mbox{d} r^{2}}{\mbox{d} r}}\cdot \frac{\partial r^{2}}{\partial x}\\&= \frac{\mbox{d} V(r)}{\mbox{d} r} \cdot \frac{x}{r},$

を利用すれば良いかもしれません．

「このように出した場の強度ベクトルの方向」と「ポテンシャルV＝一定が描く面の法線の方向」とを比較するとどうなるでしょうか？

具体的な問題をナイーブな力仕事で解くのは何度もするべきとは思いませんが，一度は指を動かして，計算する事で，「指が理論を覚えてくれる」ように感じます．自分が数学に弱いので，そう感じるだけかもしれませんが...．

Re: グラディエントとは

yama さんのレス (2007/04/28(Sat) 09:45)

>電気量をＱとすると，そこからｒの位置における電位ポテンシャルは >V=kQ/rと書けるのに対し，電場の大きさは >E=kQ/r^2と書けますよね．ポテンシャルを位置で微分すれば，とりあえずマイナスはおいといて，電場になりますよね．

その電場の方向は半径方向なので球面（等電位面）に垂直です．すなわち等電位面の法線ベクトルになっています．正確には，zoroさんのおっしゃるように３次元として計算すべきですが・・・．

>これはすなわち等電位面の微分が電場を意味することから，接線方向となるのではないでしょうか？

等電位面の微分ではなく，電位の勾配が電場になります．

簡単のため２次元の場合を考えましょう． XY平面上に電場があるとします．そのポテンシャルをφ(x,y)とし，ｚ=φ(x,y) で表される曲面を考えます．この曲面上で z=一定の点を結んだものが等電位線です．正確には，それをXY平面に射影したものというほうがいいかもしれません．要するに等高線のようなものですね．この曲面をY軸に垂直な平面で切ると切り口は曲線になりますが，その曲線の接線の傾きの符号を変えたものが電場のx成分 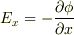$E_x=-\frac{\partial\phi}{\partial x}$ です．y成分についても同様です．電場を２次元ベクトルとして考えると，その方向は曲面の傾斜が最大になる方向なので，等電位線に垂直です．また，この方向の傾斜（曲面の傾き）が電場の大きさになります．地表の傾斜が最大になる方向が等高線に垂直であることを考えれば分かりやすいかもしれません．２次元の場合を考えたので電場は等電位線に垂直ですが，３次元の場合は等電位面に垂直になります．

なお，念のために書いておきますが，ここで扱った２次元の例では，電場はあくまでもXY平面内にあります．zは空間座標ではなく電位を表しており，長さではなく電位の単位を持ちます．

Re: グラディエントとは

みちるさんさんのレス (2007/05/02(Wed) 01:09)

みなさんのおかげで，理解ができました．「電位の山の勾配が電場」ということは，「等電位面と電場は直行する」のはある意味当たり前ですね．本当にありがとうございました．

[home] [掲示板] [ページの先頭]