無題

home > 掲示板 >

このページのPDF版

サイトマップ

無題

ハラダさんの書込 (2007/04/19(Thu) 20:02)

はじめまして，大学で現在量子の授業をとっています，レポートがでているのですが，全くわかりません．分かる方がおられましたら，教えていただけないでしょうか．よろしくお願いします．

直行系→完全系＜m|n＞＝δmn →Σ｜n＞＜n|=単位演算子

直行系から完全系の証明なんですが，わかりますでしょうか．．．どうぞよろしくお願いいたします．

Re: 無題

zoro さんのレス (2007/04/19(Thu) 21:36)

ブラケット表示は，便利なものの，馴染み難かった記憶が朧げに在りますね．

この系の任意の状態を波動関数，｜ψ＞とすると，題意より系の固有関数である規格直交系，｜n＞によって展開可能である，

｜ψ＞＝ΣAn｜n＞.

＜m｜との内積（｜m＞の共役関数との積を空間について積分）をとると，規格直交条件により，

＜m｜ψ＞＝＜m｜ΣAn｜n＞＝ΣAn＜m｜n＞＝ΣAnδmn＝Am，

となるから，任意の状態は次のように書ける；

｜ψ＞＝ΣAn｜n＞＝Σ＜n｜ψ＞｜n＞＝Σ｜n＞＜n｜ψ＞. (1)

ここで，目を閉じて，もう一度，上の右端の式を見ていると，「心の清い」あなたには；

Σ｜n＞＜n｜ψ＞＝ Σ｜n＞＜n||ψ＞＝Σ｜n＞＜n｜｜ψ＞＝{ Σ｜n＞＜n｜}｜ψ＞, (2)

と見えてきませんか？

＃うろ覚えですが，始めてこの手の話を見て；『ブラケットから「ブラ」と「ケット」に分解した造語を考えた』のは，この時では無いかと思った事があります．＃ディラックさんの興味深いのは，物理的に直截な表現が「ポット」出てくる事ですよね．まだ，幾つもの「ポット」に驚いてください．

すると，それが任意の状態｜ψ＞に式(1,2)が成立するのだから，

1＝Σ｜n＞＜n｜.

以上．

勿論，正しい証明は，ディラックさんの得意な方にバトンタッチします．

〜〜〜〜これは，厳密な解法では在りませんが，困ったら思い出してみて下さい．「完全性」の不完全な説明というべきか(笑)．

完全性

toorisugari no Hiro さんのレス (2007/04/19(Thu) 23:26)

(加算)無限次元空間は難しいので(収束とか，完備とか．．．)，厳密には関数解析を勉強してもらうか，図書館でフォン・ノイマン「量子力学の数学的基礎」，あるいは新井朝雄「物理現象の数学的諸原理―現代数理物理学入門」

http://www.amazon.co.jp/%E7%89%A9%E7%90%86%E7%8F%BE%E8%B1%A1%E3%81%AE%E6%95%B0%E5%AD%A6%E7%9A%84%E8%AB%B8%E5%8E%9F%E7%90%86%E2%80%95%E7%8F%BE%E4%BB%A3%E6%95%B0%E7%90%86%E7%89%A9%E7%90%86%E5%AD%A6%E5%85%A5%E9%96%80-%E6%96%B0%E4%BA%95-%E6%9C%9D%E9%9B%84/dp/4320017269/

を勉強してもらうしかないですが．．．

有限次元なら，一年生の範囲内のことなので簡単ですから，これで完全性を理解して，次に無限次元の完全性をおおざっぱに理解しましょう．

いま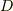次元のベクトル空間を考えます．互いに直交する単位ベクトルの組を 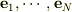$\mathbf{e}_1,\cdots,\mathbf{e}_N$ としましょう．

もし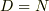，『 D=N なら，ベクトルの組 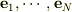$\mathbf{e}_1,\cdots,\mathbf{e}_N$ は「完全」である』といいます．これが「完全」の初等的な定義です．

例えば，3次元空間を考えましょう，3個の互いに直交する単位ベクトルの組は完全なのですが，この組があれば，高校でも習ったとおり，「任意の $\mathbf{a}$ に対して

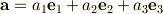
$\mathbf{a}=a_1 \mathbf{e}_1 +a_2 \mathbf{e}_2 +a_3 \mathbf{e}_3$

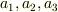となる実数の組 a_1,a_2,a_3 が存在」しますね．これはベクトルの成分そのものです．

つまり「互いに直交する単位ベクトルの組が完全なら(次元と個数が同じなら)，任意のベクトルを成分表示できる．」ということですね．(逆も成り立つのは自明ですね．)

さて，量子力学の空間は無限次元です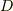．は無限だから完全な組の要素数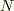も無限です．いま，ベクトルの一個足りない組を考えると N-1 も無限となり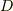，より少ないと判定できないですね．でも，明らかに不「完全」です．

個数で完全かどうかを判定するのは不適切です．つまり，初等的な定義は使えません．そこで，完全性を別の表現に変えます．先ほど，逆も成り立つと言いましたが，これを使います．

『組 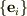$\{\mathbf{e}_i\}$ が「完全」とは任意の $\mathbf{a}$ に対して

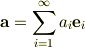
$\mathbf{a}=\sum_{i=1}^{\infty} a_i \mathbf{e}_i$

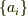となる $\{a_i\}$ が存在すること(成分表示できること)』

これが完全性の一般的な定義です．

ただ，このままでは扱いづらいので 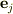$\mathbf{e}_j$ で内積をとると，直交性から，

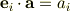
$\mathbf{e}_i\cdot\mathbf{a}=a_i$

が得られます．これを上の式に代入して，

『任意の $\mathbf{a}$ に対して

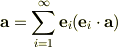
$\mathbf{a}=\sum_{i=1}^{\infty} \mathbf{e}_i(\mathbf{e}_i\cdot\mathbf{a})$

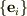なら組 $\{\mathbf{e}_i\}$ は完全．』を完全性の新しい定義とします．

この表示をブラ・ケットで書き換え，右辺の $\mathbf{a}$ をのぞいた部分を演算子とみれば，題意の式になりますね．

Re: 完全性

ハラダさんのレス (2007/04/25(Wed) 03:04)

ありがとうございました．なんとか，解決しました．

量子力学を勉強し始めたばかりで，分からないところが多いですが，なんとか理解できるようになりたいと思います．

[home] [掲示板] [ページの先頭]