あの有名な式
あの有名な式
盾矛 さんの書込 (2007/04/19(Thu) 09:16)
アインシュタインの有名な式
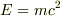 がありますが,
この式の導き方が詳しく載っているサイトはありませんか?
本を買って勉強したのですが,
「なんでいきなりこの式が出てきたの?」とか
「この式からこの式へはどんな理由で変換できたの?」
とか多々疑問がわいてしまいました.
がありますが,
この式の導き方が詳しく載っているサイトはありませんか?
本を買って勉強したのですが,
「なんでいきなりこの式が出てきたの?」とか
「この式からこの式へはどんな理由で変換できたの?」
とか多々疑問がわいてしまいました.
もしも簡単に説明可能ならここで解答をいただけると嬉しいですが, きっと簡単なわけないでしょうから サイトをじっくり読んで勉強したいと思います.
宜しくお願いします.
Re: あの有名な式
盾矛 さんのレス (2007/04/20(Fri) 09:40)
ありがとうございます.
教えて頂いたサイトも以前見たことがあったのですが,
「右辺の第2項は運動エネルギーの式に似ている…」
と言う内容から導き出しているようですが
「第2項だけで安易にエネルギーとしてしまっていいの?」
と疑問がわいてしまいました.
最初に 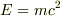 を見つけた人はどのような手順で導き出したのでしょうか?
を見つけた人はどのような手順で導き出したのでしょうか?
Re: あの有名な式
イレフト さんのレス (2007/04/20(Fri) 22:06)
アインシュタインの関係式は特殊相対性理論でニュートン力学を4次元に拡張した結果得られるものです. 詳しく知りたいんでしたら,やっぱり本を開くのが一番でしょう.
式の変換がわからないんでしたら,どこがどうわからないのか,具体的に質問したらどうでしょう? ローレンツ変換がわかって4元運動量が理解できているなら話はわりと簡単かと..
Re: あの有名な式
盾矛 さんのレス (2007/04/21(Sat) 13:23)
ありがとうございます.本を買い漁ってみます. そこでまたわからない式があった場合に質問させていただきます
Re: あの有名な式
盾矛 さんのレス (2007/04/21(Sat) 14:33)
いきなりなのですが,
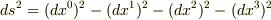 で,なぜ
で,なぜ 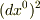 だけ符号が逆なのでしょうか?
だけ符号が逆なのでしょうか?
Re: あの有名な式
イレフト さんのレス (2007/04/22(Sun) 01:14)
その式は光速度不変の原理を表すために導入されたものです.
光速度不変の原理はまあ,あらゆる慣性系で光の速度Cが変わらないというものでしたね.なので原点に置いたライトから出る光の波面は二つの慣性系 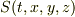 と
と 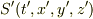 ではともに
ではともに
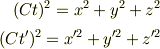
となるはずです. ここで
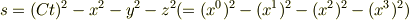
というsを考えると要するに光速度不変の原理を満たすには慣性系 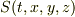 と
と 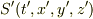 でこのsの値が一緒ならいいわけです.そこからローレンツ変換を導いていくわけですが…
だからsの中で
でこのsの値が一緒ならいいわけです.そこからローレンツ変換を導いていくわけですが…
だからsの中で 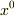 と
と 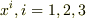 で符号が違うのはもともとが
で符号が違うのはもともとが
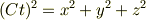
から出発しているからです. ここから超弦理論なんかでは時間と位置の違いは位置は実数,時間は虚数の方向に進んでいる…なんて考えるらしいですが,まあそのへんを突き詰めるときりがないので..
Re: あの有名な式
盾矛 さんのレス (2007/04/22(Sun) 02:38)
ありがとうございます.
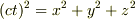 なら
なら
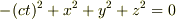 にはならないんでしょうか?
僕の頭の中では半径ctの球があって,
にはならないんでしょうか?
僕の頭の中では半径ctの球があって,
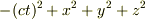 は常に0というイメージがあります.
光ではなく止まっている物質に対してはct軸のメモリだけが爆発的に増えて,
は常に0というイメージがあります.
光ではなく止まっている物質に対してはct軸のメモリだけが爆発的に増えて,
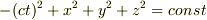 にはならない気がします.
理解できてない状態で質問してるので質問が伝わるかどうか不安ですが
よろしくおねがいします.
にはならない気がします.
理解できてない状態で質問してるので質問が伝わるかどうか不安ですが
よろしくおねがいします.
Re: あの有名な式
佑弥 さんのレス (2007/04/22(Sun) 14:40)
はじめまして,佑弥と申します.
エネルギーに似ているから,安易にエネルギーにしてよいか,という 質問のところが少し気になったので,コメントさせてください.
相対性理論はニュートンの力学理論を光速に近い状態でも成り立つように 書き直したものですから,相対性理論以前の理論体系から何の飛躍もなし に導くことはできません.(その飛躍を行ったことで私たちに新しい理論 が与えられるのです.) やはり,最後はその理論で予測されることが実験に一致するかどうかによっ て確認しなければ,物理としては無意味なものとなってしまいます.
逆に言えば,速さが遅い状態では,ニュートンの力学で現象の予測ができた わけですから,新しい理論もその極限でニュートンの力学にほぼ一致する はずだ,という信念を持つことができるわけです.
実際に特殊相対論の創始者たちが,いかに考えていたのかは僕にはわかりま せんが,古典理論との対応関係などを元にこれはエネルギーに対応するだろう, 運動方程式はこの形になるだろう,等と予測しながら理論を構築していった のではないかと僕は思います.
Re: あの有名な式
小林@那須 さんのレス (2007/04/22(Sun) 15:37)
>最初に E = m c^2 を見つけた人はどのような手順で導き出したのでしょうか?
本や有名なサイトに書いてあるだけで分った気になるのではなく,自分で納得 できるまで考え抜こうとする姿勢が,私は好きです.
さてエネルギーではなく運動量で考えることと,静止している物体は,四元 時空間では光速度で時間軸方向に進んでいると見なすことで盾矛さんの問題 提議に対し直感的な説明が可能です.
時空間:Minkowsky 空間では時間と空間を同じ単位次元で理解すべきです. 距離を `meter で捉えるならば,時間も `meter で捉えるべきです.私自身 は相対論の時間は `lMeter(light meter の意味で,1`meter の距離を光が進 む時間) と捉えています.こう捉えることで,位置の時間変化 x(t) は時空 間での幾何学と見なせます.そのとき時間軸を純虚数と捉え,光の速度を無 次元の i と捉えるべきだと私は主張します.(ここらになると異論も出てき そうですが)
こう捉えることにより Lorentz 変換は無次元の回転変換行列になります. Lorentz 変化を虚数角度の回転変換と捉えることができます.時計が遅れた り,物差しが縮んだりする現象は,直角三角形のピタゴラスの定理を虚数も 含んだ時空間まで拡張したものと見なせます.
ここで,四元運動量を考えます.そして質量 m の物質が静止していることを 時間軸方向に m `c の運動量成分で走っていると見なしてやります.即ち静 止している物体などないと考えてやるわけです.後は,それで整合性が取れ るか否かの問題になります.
時間成分を <c t, x> から <t,x> のように `c の単位次元の差を付けた状態 にすると四元運動量の時間成分はエネルギーの単位次元隣 <m c^2, 0,0,0> と なります.一つ整合性が取れました.
2`kg の物体が,光速度の 1e-8i の遅い速度で動いているときの運動量を, 先の虚数角度と,無次元の Lorentz 変換虚数回転から計算させて見ましょう. 下のように四元運動量ベクトル -2e-8 の空間速度成分が出てきます.この意 味でも静止している質量 m の物体は <m `c i, 0,0,0> の四元運動量を持つ と解釈できます.ここでも整合性が取れます.
v = 1e-8i, θ = !atan(v )
v = 1e-8i, m=2`kg, θ = !atan(v ), @Rt(θ)<m 1`meter/1`lMeter,0> v = 1e-8i, m=2`kg, θ = !atan(v ), @Rt(θ)<m i `meter/1`lMeter,0> < 2i, -2e-008 >
ここで Rt は下のような回転行列を返させる関数です type Rt.sf θ @= _prm{1} _rt =[[2]] _rt[0,*] = <!cos(θ),-!sin(θ)> _rt[1,*] = <!sin(θ), !cos(θ)>
ここで,何でエネルギーが 1/2 m `c^2 ではなく m `c^2 なのだという疑問が 出てくると思います.一方で E = ∫v dp ( v が c に近づくと速度は c で 飽和するから E ≒ p c )です.静止質量とは時間軸方向に光速度で飛んでいる 状態での質量と解釈できます.ここでも整合性が取れています.
静止している質量の大きな物体を動かし難いのは,時間軸方向に光速度で m `c の運動量で飛んでいる物質の運動量の向きを変化させるときに抵抗があ るからだと解釈できます.ここでも整合性が取れます.
静止していることを光速度 `c で走っているとすると,質量が無限大になら ないかとの矛盾点も指摘できます.でも,元々質量が 0 だったものが何らか の機構で光速度で時間を止めたまま空間を飛んで行くようのになった,即ち 時間軸方向に飛んでいくために質量が付与されたと考えれば,質量が有限で 時間軸方向に光速度で飛んでいくのも矛盾しません.どのみち質量なんて, 未だ明確に説明されているものではないのですから.
私自身も盾矛さんと同じように特殊相対論が解らんと思っていた時期があり ました.今は,ここに書いたように解釈して納得しています.このよに解釈 してから,特に矛盾点に突き当たっていません.まだ途中ですが下の拙稿も 読んでいただければと思います.
Re: あの有名な式
イレフト さんのレス (2007/04/22(Sun) 18:43)
ながながとなってしまっているところ恐縮ですがとりあえず2007/04/22(Sun) 02:38 No.15407の質問の答えを.. そのとおりですね.
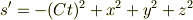
と考えても別にかまいません.本によってはこっちのものもあるんではないでしょうか?ただ,この場合,光より遅く運動する物体を考えたときにs'<0なんでめんどくさいですね.ので普通こちらを取らないのでしょう.
さて,このsは盾矛さんのいうように当然光のとき(s=0)以外一定ではありません. このsが意味を持つのは二つの慣性系で比較したときだけです. 二つの慣性系での
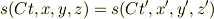
が成り立っていることが大事であってその値は普通一定にはなりません.
Re: あの有名な式
佑弥 さんのレス (2007/04/23(Mon) 08:46)
ちなみに,世界距離を
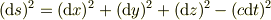
と定義することによるメリットもありますので,少し補足をさせてください. すぐに思いつくのは,ある慣性系で同時におこったことの距離をユークリッド的な距離として 表せることでしょうね.そのとき,ローレンツ変換しても世界距離の値は変化しませんから, 距離を正として表すことができます.
もちろん,運動を記述しようとすると値が負となって気持ち悪いですが,固有時の自乗を世界距離の
自乗に 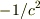 をかけたものと定義することで,通常通り記述できます.
をかけたものと定義することで,通常通り記述できます.
Re: あの有名な式
盾矛 さんのレス (2007/04/24(Tue) 09:06)
熟読していたため,返答が遅れました. みなさんありがとうございます.感動しました.
>佑弥さん もちろん飛躍は必要ですが, その飛躍を他人に納得させるためには確固とした証明が必要だと思いました. その証明方法は何かなぁ?と思い質問させて頂きました.
>小林@那須さん 激しく難しいです… でも,ありがとうございます. ゆっくり,かつ,じっくりと読ませて頂きます.
>イレフトさん なるほど.表現が難しいですが, 「ある瞬間の四次元的な長さ」が等しい… みたいな感じでしょうか… とても表現が難しいですが,なんとなく理解できた気がします.