のんたん さんの書込 (2007/04/13(Fri) 17:25)

熱力学についての質問です． 風と温度についてどうも分からないことがあります．

【例】 室温：20℃の中で，風を起こします（極力発熱しない機械やうちわなどで）室内の空気には運動エネルギーが与えられ移動します（これが風）． そのときの温度は上昇するのでしょうか？

どなたかご回答とその理由をお願いします．

クロメル さんのレス (2007/04/15(Sun) 08:00)

空気は粘性流体ですから，風を起こすと粘性摩擦によりマクロな風の動きは散逸しミクロな分子の速度になります．よって温度は上がると思います．どの程度上がるか見積もってみます．

まず，分子の速度ｖをどの程度か計算します．

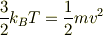
空気分子は分子量３０くらいですから，一分子あたりの重さｍ（ｋｇ）は，５×１０＾‐２６くらい．室温は，T=３００（K）ボルツマン定数は，１．３×１０＾−２３ですから，ｖ＝√４×１０＾５＝５×１０＾２（ｍ）くらいになります．（これは３０１．５（℃）にあたります．） 速度のx方向成分は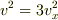， より２．８８×１０＾２（ｍ）です．

ｘ方向に風をおこすとき，速度のx方向成分が＋５（ｍ）くらいされるとすると， 速度はｖ＝√（２８８＾２＋２８８＾２＋２９３＾２）＝５０２（ｍ）

再び

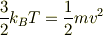
の式にｖ＾２を代入して，Tを何度に相当するかもとめてみると， ３０４（ｍ）になりました．

２．５℃上昇するという結果がでましたが，実際には５ｍ/ｓ加速されるのは ，一部の分子であってそれが温度上昇した分子と交じり合うことから実際の温度上昇はもっと少なくなると思います．

ちなみに風でものを冷やすことができるのは，全体として重心が移動する風はまだ速度が散逸する前なので，温度は室温のままであるからです．２．５℃上昇するのは，散逸が起こった後であることに注意してください．

とここまで書きましたが．本当にそんなに温度があがるものなのかというのが私の感想です．頼りない意見ですいません．

クロメル さんのレス (2007/04/15(Sun) 08:12)

すいません．よく考えたら平均速度５００（ｍ）というのは，正の方向と負の方向両方に向かう分子があるので，正の方向に５（ｍ）加速しても一方は５０５（ｍ） になり加速されますが，もう一方は４９５（ｍ）に減速されるので，結局平均は５００（ｍ）のままです．

ということは，もうちょっと厳密に計算してやらないといけません．（二次の微小量まで考慮）上で言ったことは，間違ってます．ほとんど温度は上昇しないと思っていいでしょう．

分子速度を大雑把に見てみると，

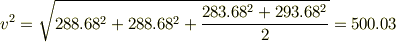
より ０．０４℃上がるっていうことになりますね．

小林＠那須 さんのレス (2007/04/15(Sun) 09:27)

元の計算の方が正しいと考えます．絶対零度で 5`meter/sec の速度を与えた ときを考えれば良いでしょう．500`meter/sec と -500`meter/`sec の二つの 粒子に 5`meter/`sec の速度を追加したときの差でも下のように計算できま す．

sf "v=500`meter/`sec, Δv=5`meter/`sec, 1/2(v+Δv)^2 + 1/2(-v+Δv)^2 - ( 1/2 v^2 + 1/2(-v)^2 ) == 2 (1/2 Δv^2)" < 0 >

>本当にそんなに温度があがるものなのかというのが私の感想です．

空気の比熱が小さいので正しいと思います．蛍光灯の中のプラズマが 10 万 度というのと似たような話です．

水素原子で計算し直してみました．

sf "T=273, v=!sqrt(3 `kB T/`HM)" < 2599.4 > # 単位は `meter/`sec です

sf "T=273, T (5`meter/`sec) / v" < 0.525122 >

0 度C で 2600`meter/`sec の速度であり，5`meter/`sec の追加で 0.5 度の 上昇です．

なお上の計算は拙作の sf.exe と名付けたソフトで行っています．ウィンド ウズ・コンソールで上の "...." 文字列を引数に実行させます．日常使う数 式計算にできるだけ近づけてあり積演算子 * は省略可能です．上のように変 数文字列や 単位文字列付きで計算式を扱えるのが自慢です．sf.ini という ファイルに変数を登録しておくことで任意の文字列変数値を使えます． `kB： ボルツマン定数，`HM：水素原子の質量を登録済みだったので，水素原子で計 算しました．

下にマニュアルがあります．

• http://www.nasuinfo.or.jp/FreeSpace/kenji/sf/fastTour/sfFastTour.htm

単なるコマンド・ライン・プログラムであり，エディタのマクロに組み込ん で使うことを想定しています．私自身は Wz Editor マクロに組み込んで Wz コンソールで実行させています．

sf はギリシャ文字変数，行列の加減乗除算，fft やグラフ表示も可能です． パウリ行列`σx, `σy, に対して，下のような計算も可能です．

sf "t=0.13`sec, ~expM(t `σx + (3+i) `σy)" < 5.46048 +8.44666i, 8.80736 -5.16525i > < -8.16353 +5.68605i, 5.46048 +8.44666i >

上の水素空気の計算では，左値変数 v を置くことで v.val という計算結果 の入った変数ファイルをカレント・ディレクトリに作らせています．それを 二つめの式で利用しています．物理の計算のように試行錯誤しながら色々と 試すのに便利にしてあります．物理の計算でしたら Mathematica より重宝す るはずです．こちらも見てやってください．

小林＠那須 さんのレス (2007/04/15(Sun) 11:23)

すいません，温度・エネルギーの線形加算性からすれば下のようになります． 単位を付けていないと計算間違いをやらかしてしまいます．

1/2 `HM Δv^2 == 3 1/2 `kB ΔT より温度上昇 ΔT は下のようになります．

sf " Δv = 5`meter/`sec, ΔT = `HM Δv^2/(3 `kB)" < 0.00101008 >

温度上昇は 1/1000 度でした．

質量 m = 5e-26 `kg, のときは sf "m = 5e-26`kg, Δv = 5`meter/`sec, ΔT = m Δv^2/(3 `kB)" < 0.0301788 >

です．0.03 度の温度上昇でした．