積分の平均値の定理
積分の平均値の定理
けん(大学新2年) さんの書込 (2007/04/13(Fri) 16:22)
ふと思い浮かんだ疑問です.
a<bとします. 積分の範囲は(a,b)とし,以下では略します.
a<c<bを満たすあるcが存在して,
∫f(x)dx=(b-a)f(c)
である.(証明は略します.)
このとき,上式を変形して,
f(c)=∫f(x)dx/(b-a)
です.これは,f(c)が,(a,b)でのf(x)の平均値であることを意味しているのでしょうか.
よろしくお願いします.
Re: 積分の平均値の定理
クロメル さんのレス (2007/04/15(Sun) 06:55)
けんさんのおっしゃる通りだと思います. 高校のときにその微分形はならいましたよね. aからbの間のグラフを書き,さらに平均の値を引くと,そのグラフは少なくとも一回以上交わるってことになると思います.
Re: 積分の平均値の定理
けん(大学新2年) さんのレス (2007/04/16(Mon) 13:00)
レスありがとうございます.
(a,b)でのf(x)の平均値は,
f(c)=∫f(x)dx/(b-a)
で定義されるということでよろしいのですか?
Re: 積分の平均値の定理
toorisugari no Hiro さんのレス (2007/04/16(Mon) 14:08)
言葉の問題にすぎませんが,
「
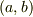 での
での 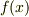 の平均値
の平均値 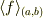 は,
は,
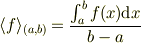
で定義される.
平均値の定理とは,
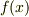 が連続なら,
が連続なら, 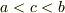 で
で
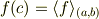
となる  が存在する事を指す.
」
が存在する事を指す.
」
定義と定理をごっちゃにされているような..
Re: 積分の平均値の定理
けん(大学1年) さんのレス (2007/04/18(Wed) 23:02)
>定義と定理をごっちゃにされているような..
ごっちゃになっていたようです.でも,おかげさまで理解できました. toorisugari no Hiroさん,ありがとうございました.