∞
∞
touy さんの書込 (2007/04/08(Sun) 05:27)
数学の質問なんですが,教えていただけないでしょうか?
lim{n→∞}a_n=∞,lim{n→∞}b_n=∞のとき lim{n→∞}(a_n+b_n)=∞,lim{n→∞}(a_n×b_n)=∞
これを数学的に証明することは可能でしょうか?可能ならば証明の方法を教えてください.お願いします.
Re: ∞
佑弥 さんのレス (2007/04/08(Sun) 15:30)
touyさん,はじめまして.佑弥と申します.
解答をしたいと思うのですが,どのレベルでの 解答を期待されていますか?(高校レベルでいい のか,厳密に証明してほしいのか等々)
Re: ∞
佑弥 さんのレス (2007/04/08(Sun) 15:45)
一応証明しておきます.
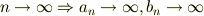
であるが,この式を以下のように言い換えることができる.
任意の正の実数a,bに対して
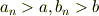
となる整数nが存在する.
このとき,
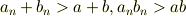
となりますから,a+b=c,ab=dと書き直せば,任意の正の実数c,dについて
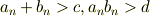
となるnが存在しますから,題意が示されます.
Re: ∞
touy さんのレス (2007/04/08(Sun) 20:29)
佑弥さん,返信ありがとうございます. 自分は高校生なので,上の説明は非常にわかりやすかったです. 厳密的な証明は,ε-N法と呼ばれる方法を使うのでしょうか?
Re: ∞
佑弥 さんのレス (2007/04/08(Sun) 22:06)
分かっていただけてよかったです. 上の証明で十分だと思いますよ.∞の定義そのものを使っていますからね.後は論理記号を使ってきちんと書けば曖昧さが回避できるぐらいでしょうか. といっても僕は大学に入ったばかりなので変なことを言っていないかドキドキしています(笑)
Re: ∞
yama さんのレス (2007/04/08(Sun) 23:45)
定義がちょっと違っているように思います.
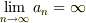 というのは,「任意の正の実数
というのは,「任意の正の実数  に対して,整数
に対して,整数 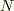 が存在し,
が存在し, 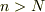 のとき
のとき 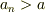 になる.」ということだと思います.
佑弥さんの証明をこの定義に合うように修正することは容易でしょう.
になる.」ということだと思います.
佑弥さんの証明をこの定義に合うように修正することは容易でしょう.