早い物
早い物
盾矛 さんの書込 (2007/04/07(Sat) 14:29)
ローレンツ変換した際,
![x^{'} = \frac{x-Vt}{\sqrt[]{\mathstrut 1-V^{2}/c^{2}}},](http://hooktail.maxwell.jp/bbslog/92dd2c0db792c08cc0ebf63f1c5919bb.png)
![t^{'} = \frac{t-Vx/c^{2}}{\sqrt[]{\mathstrut 1-V^{2}/c^{2}}}](http://hooktail.maxwell.jp/bbslog/ebc3b1a4a43b69a24c34b376ab16f3a6.png)
になるのですよね? だから,Vが逆方向(向かってくる)場合は, V<0 になって,x'はxに比べて大きくなる,t'はtに比べて大きくなる (物は伸びて,時間は早く進む) で合っていますか?
Re: 早い物
ミュフ猫 さんのレス (2007/04/07(Sat) 15:02)
こんにちは. 長さや時間の比を比較するなら,微分係数で比較すべきではないでしょうか? 例えば,
dx'/dx ,dt'/dt
というように.良くわかりませんが.w
ローレンツ収縮(Re: 早い物)
toorisugari no Hiro さんのレス (2007/04/07(Sat) 20:55)
原点に一端がある「静止」した長さ  の棒を考えましょう.
の棒を考えましょう.
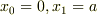 とおくと,同時刻
とおくと,同時刻 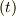 におけるそれぞれの端はローレンツ変換で
におけるそれぞれの端はローレンツ変換で
![x_0^{'} = \frac{x_0-Vt} {\sqrt[]{\mathstrut 1-V^{2}/c^{2}}},\,t_0^{'} = \frac{t-Vx_0/c^{2}}{\sqrt[]{\mathstrut 1-V^{2}/c^{2}}},\\x_1^{'} = \frac{x_1-Vt} {\sqrt[]{\mathstrut 1-V^{2}/c^{2}}},\,t_1^{'} = \frac{t-Vx_1/c^{2}}{\sqrt[]{\mathstrut 1-V^{2}/c^{2}}}](http://hooktail.maxwell.jp/bbslog/a74aad11a5b15270f79023a5a1088c4a.png)
に移ります.
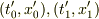 の世界線は
の世界線は  を消去して
を消去して
![x_0'+Vt_0'&=0\\x_1'+Vt_1'&=a\,{\sqrt[]{\mathstrut 1-V^{2}/c^{2}}}](http://hooktail.maxwell.jp/bbslog/766ecfd2bcaffbffeb0c0df7ede477e2.png)
となるので,「動いている」系からは世界線の空間的距離は ![a\,{\sqrt[]{\mathstrut 1-V^{2}/c^{2}}}](http://hooktail.maxwell.jp/bbslog/3a2cb508e4835b1e344cae57ed6ea5da.png) となり縮んで観測されます.これは速度の符号によりません.
となり縮んで観測されます.これは速度の符号によりません.
時間に対しては
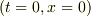 は
は 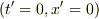 に,
に,
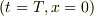 は
は ![(t'=\frac{T}{\sqrt[]{\mathstrut 1-V^{2}/c^{2}}},x'=\frac{-VT} {\sqrt[]{\mathstrut 1-V^{2}/c^{2}}})](http://hooktail.maxwell.jp/bbslog/ae2612b6eae6cf9e9b578f900204014a.png) に,
移るので,時間の進みが遅く
に,
移るので,時間の進みが遅く ![T\to\frac{T}{\sqrt[]{\mathstrut 1-V^{2}/c^{2}}}](http://hooktail.maxwell.jp/bbslog/e7d2eeb26db29818cad461e3fff661ff.png) 観測されます.これも速度の符号によりません.
観測されます.これも速度の符号によりません.
Re: ローレンツ収縮(Re: 早い物)
盾矛 さんのレス (2007/04/07(Sat) 22:49)
ありがとうございます.
xの方は理解できました. tの方について,もう少しだけ質問させて下さい.
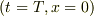 という条件は,原点について論じていますが,
原点から離れた場所
という条件は,原点について論じていますが,
原点から離れた場所
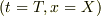 で速度
で速度 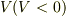 では
では
![(t^{'} = \frac{T-VX/c^{2}}{\sqrt[]{\mathstrut 1-V{^2}/c{^2}}}),](http://hooktail.maxwell.jp/bbslog/de460744caaa4dcf6dea59a0a4bf72db.png)
![(x^{'} = \frac{X-VT}{\sqrt[]{\mathstrut 1-V{^2}/c{^2}}})](http://hooktail.maxwell.jp/bbslog/c654d642ee65b60f66ede9fcee219ed0.png) で,
で, 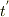 は
は 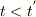 になり,やはり時間が進む気がします.
になり,やはり時間が進む気がします.
上記に関してどのようになるでしょうか.
Re: ローレンツ収縮(Re: 早い物)
toorisugari no Hiro さんのレス (2007/04/09(Mon) 12:14)
「時刻」が原点方向に変化することと,「時間」が短くなることを混同されています.上の式は時刻の式です.ローレンツ収縮を考えるためには時間で考えてください.