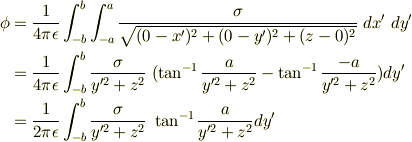電磁気学の問題

$\phi &= \frac{1}{4 \pi \epsilon} \int_{-b}^b \int_{-a}^a \frac{\sigma}{\sqrt{(0-x^\prime)^2+(0-y^\prime)^2+(z-0)^2}}\ dx^\prime \ dy^\prime\\&= \frac{1}{4 \pi \epsilon} \int_{-b}^b \frac{\sigma}{y^{\prime2}+z^2}\ ( \tan^{-1}\frac{a}{y^{\prime2}+z^2} - \tan^{-1}\frac{-a}{y^{\prime2}+z^2} )dy^\prime\\&=\frac{1}{2 \pi \epsilon} \int_{-b}^b \frac{\sigma}{y^{\prime2}+z^2}\ \tan^{-1}\frac{a}{y^{\prime2}+z^2} dy^\prime$

ですから，これが，計算できるかどうかですね．

Re: 電磁気学の問題

zoro さんのレス (2007/04/04(Wed) 21:32)

横から失礼します．

少なくとも，zが小さくて，x,yも其の長方形の中心の近くなら電場は一定値に漸近しますね．また，其の長方形のサイズよりも十分に遠方なら全電荷，σab，をもった点電荷の振る舞いに漸近しますね．検算に使えます...，てご存知ですよね，こりゃまたしつれいしました(植木等さんを偲んで)．

電場は，ｙamaさんの方針で出すのが最速と思いますが，その積分は初等関数では表現できないと思います．クロメルさんの処方で，zの偏微分を取ると簡単になると良いですが...，最近，指に力が入らなくなってしまった．

＝＝＝＝ｙamaさん，便乗質問です．

このページは"Mac"で書いています．HNを前のところからコピー＆ペーストしています．この場合，「ｙ」と「a」には半角の空白があるように見えます．ところが，"Windows"で見ると，「yama」にしか見えません．恐らく，"Mac"での全角の「ｙ」が正しいと推測しております．

ブラウザは両者とも"Firefox 2.0.0.3"を使用しております．もし宜しければ，どちらか正しいかをお教え下されば幸いです．もし個人情報の関係で問題があれば，この便乗質問部分は撤回いたします．

Re: 電磁気学の問題

yama さんのレス (2007/04/04(Wed) 23:09)

yは半角ですが・・・全角でも別に差し支えはありません．

Re: 電磁気学の問題

zoro さんのレス (2007/04/04(Wed) 23:20)

ご回答有り難うございました．以後は，半角で記入致します．

[home] [掲示板] [ページの先頭]