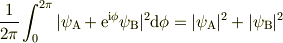電子の波動性について

home > 掲示板 >

このページのPDF版

サイトマップ

電子の波動性について

あすかさんの書込 (2007/04/02(Mon) 12:47)

量子力学で疑問に思ったので質問させていただきます．よろしくお願いします．

１つのスリットがあるところに１つの電子を飛ばすとスリットの後ろの検出版には電子が１点検出されて，それを多数回行うと ψの２乗の模様を描き出すと習いました．

２つのスリットがあるところに電子を１つ飛ばすと同じようにスリットの後ろの検出版には電子が１点検出されて多数回行うと(ψA＋ψB)の２乗の模様を描き出すと習いました．

では，２つのスリットのうち，片方(B側)にだけ検出装置を設置しておき， Bを通ったものは無視して， Bを通らなかったものだけを多数回検出するとどのような模様になるのでしょうか？１つのスリットのみを通っているのでψの２乗になるのでしょうか？それともスリットは２つあるので(ψA＋ψB)の２乗に近い模様になるのでしょうか？教えて下さい．お願いします．

Re: 電子の波動性について

zoro さんのレス (2007/04/03(Tue) 02:37)

あすかさん，始めまして．

あまり自信がありませんが，一つの考え方を書いてみます．

所謂，「マクスウェルの悪魔」見たいに都合のいい番人がいて，Bのスリットに来る電子を何の撹乱も無しに検知して，その結果をスリットの後ろの検出側に意味のある情報，言い換えれば「今の電子はスリットBを経由して来たから，データ蓄積をするな」と検出系に伝達でき，さらに検出系が「この情報を元にデータ蓄積をしないこと」が原理的に可能かどうかに因るのではないでしょうか？

Re: 電子の波動性について

あすかさんのレス (2007/04/03(Tue) 10:41)

お返事ありがとうございますそしてはじめまして

検出装置の影響をうけても構いません．電子１つを飛ばして後ろの検出版に検出されたとき，スリットの検出装置に反応した場合は記録せず，スリットの検出装置に反応しなかった場合は逆側のスリットを通ったことになるため記録しますその実験を多数回繰り返して検出版のデータを全て重ね合わせるとどのような模様になるのでしょうか？

Re: 電子の波動性について

EMAN さんのレス (2007/04/03(Tue) 12:26)

はじめまして．なかなか良い質問だと思いました．

私なりの考えですので，おかしいと思ったら遠慮なく反論して下さい．

電子がBを通ったら，必ず分かる．よって，ターゲットに当たる電子は必ずAを通ってきた．よって，ψAの模様になる・・・．

それとも，「Bを通ろうとしてまだ検出器につかまる前の波」との間で干渉を起こすので，像は影響を受けるのか？そんな疑問かと思います．

しかしそもそも，このような装置を組む事が可能か？ Bを通れば必ず分かるということは，Bを抜けたところからは，必ず検出器に当たるように，検出器ですっぽり包まなくてはならない．つまり，仕切りとなっている．すると，Aとは元から干渉しようが無いから，スリットBは無かったも同じ．

思考実験の図に良くあるように，仕切りなど設けずに光を当てて調べるとしたら，その光はスリットAを通ってきた電子にも当たりはしないか．

つまり，現実的にこの実験は出来ないのでは？という答えですが，いかがでしょう？

Re: 電子の波動性について

あすかさんのレス (2007/04/03(Tue) 14:50)

お返事ありがとうございますはじめまして疑問はまさしくおっしゃった通りですここに投稿する前に本や他サイトを使用して調べたのですが， B側に検出機を置いた時は波動が乱れるとありました Bに検出機を置いた影響だと思います具体的にはこのサイトを参考にしました

http://homepage2.nifty.com/einstein/contents/relativity/contents/relativity3156.html

乱れるからには，Bを通った電子も後ろの検出版には到達できていると思いましたサイトに書いてあることを自分が理解しきれなかったのかもしれませんが．ならば，Aだけを検出した場合は，１つだけのスリットの場合と同じになるのか， Aを通った電子がBのスリットをあることを知って干渉の模様を描くのか知りたかったのです宜しくお願いします

Re: 電子の波動性について

zoro さんのレス (2007/04/03(Tue) 17:08)

横から失礼します．

ご紹介のサイトの資料，ないしはそこで引用されている本などを勉強したいと思います．それを確認して，自説と合わせてから出直したいと思います．

なお，上記のサイトは，他の論議でも引用させていただきました．興味深いのですが，ここまで詳しく引用するのには，いささか抵抗を覚えます．これも検討したいと思います．

論議を続ける事が出来ず，ご免なさい．

Re: 電子の波動性について

EMAN さんのレス (2007/04/03(Tue) 18:21)

なるほど，先ほど，現実的には実験は無理と書きましたが，スリットに通す前の段階で電子を二通りの道に分けておいて，一方の経路で測定してから，二つの経路をそれぞれのスリットへと導けば良いわけですね．

このとき，もし，Bで検出された場合のみを集めれば，スクリーンには ψB のみの模様が映りますね．

ではBで検出されなかった時にはどうなるか．二通りに分けた瞬間に，どちらかに分かれるのではありませんね．量子力学では途中の運動を論じることが出来ません．

B経路を通ったから検出器に掛かるわけではなく，検出器に掛かった時点でB経路を通った事が確定するわけです．

すると，途中で検出されなくても，電子は両経路の存在は感じ取っているわけですね．すると，ψAではなく，少し撹乱をうけるだろうと予想は付きます．

書いている途中で分からなくなって少し迷いましたが，これが私の考えです．

Re: 電子の波動性について

あすかさんのレス (2007/04/04(Wed) 08:55)

みなさん大変ありがとうございます検出機にかからなくても両方の経路を感じているということは測定結果はψAの２乗のから少し乱れた波形ではなく，(ψA＋ψB)の２乗が乱れた波形になると思っていいでしょうか？

Re: 電子の波動性について

MXK さんのレス (2007/04/04(Wed) 11:57)

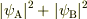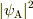まず，Bに検出器を置いた段階で， $|\psi_{\rm A}|^2+|\psi_{\rm B}|^2$ となって干渉縞が消えます．検出結果を利用して，Bを通った場合を除くということは，スリットBを閉じた場合と同じことなので， $|\psi_{\rm A}|^2$ となります．

Re: 電子の波動性について

EMAN さんのレス (2007/04/04(Wed) 12:55)

MXKさんのように断言されてしまうと続けづらいのですが，あえて挟ませてください．私以外にも参加してくださってほっとしています．間違いがあったらご指摘願います．

もしBに検出器があっても，感度がゆるゆるであったなら，ほとんどBの検出器は無いも同然だということになり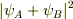， $|\psi_A + \psi_B|^2$ に近付く気がします．例えば，検出のための光の照射を非常に弱くするとかして「見逃し」を許せば，そうなるのではないでしょうか．

で，感度を上げていけば，そのためにはB経路を完全に塞がざるを得なくなり， MXKさんの言われる通りに，（また最初に私も言ったように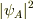） $|\psi_A|^2$ となる，という考えです．

本当は別の内容を書き込むつもりで用意していたのですが， MXKさんの書き込みを見て少し意見を修正しました．これでどうでしょう．

Re: 電子の波動性について

MXK さんのレス (2007/04/04(Wed) 14:53)

> もしBに検出器があっても，感度がゆるゆるであったなら， > ほとんどBの検出器は無いも同然だということになり問題の設定からして，まずは完全な検出器の場合を考えるのが適当だと思います．つまり，透過率も1，検出確率も1，という検出器です．

>で，感度を上げていけば， > そのためにはB経路を完全に塞がざるを得なくなり，経路を塞がなくても，Bを通過したことを確実に知る仕組みは（少なくとも原理的には）ありますから，ここはちょっと違うと思います．

Re: 電子の波動性について

あすかさんのレス (2007/04/05(Thu) 12:10)

貴重なご意見ありがとうございます

B側に設置した検出機で検出を行った際，電子が後ろの検出版に到達できる検出方法があれば，検出しなかった電子(A側を通ったではず)の描く模様は (ψA＋ψB)の２乗の乱れた波形を描き， Bを通った事を検出するためにB側を塞がなければならない場合は ψAの２乗に近い波形を描くということでよろしいでしょうか？

Re: 電子の波動性について

zoro さんのレス (2007/04/05(Thu) 14:09)

＞経路を塞がなくても，Bを通過したことを確実に知る仕組みは（少なくとも原理的には）ありますから，

このように主張される場合は，「どのような原理的構成により検出可能である」かを示さないと，論議にならないようにおもいます．

私には，「A」を通る場合にはなにもせず，「B」をとおった場合，100%検出し，スリット後方の記録系にその情報を伝達することは想像できませんでした．

ぜひとも，その様な仕組みをお教え下さいませんか？

Re: 電子の波動性について

MXK さんのレス (2007/04/05(Thu) 14:27)

あすかさん，

いえ，どちらの場合も $|\psi_{\rm A}|^2$ です．

この辺りは朝永先生の「光子の裁判」でも読んでいただくのが，早道かと思います．

Re: 電子の波動性について

ＥＭＡＮさんのレス (2007/04/05(Thu) 22:44)

しばらく考え込んでおりました．

MXKさんの言われる，「経路を塞がなくても，Bを通過したことを確実に知る仕組み」はありそうですね．

ただ私に思いつくのは厳密に100%ではなく，「ほぼ確実に」くらいのものです．

検出器を，経路Ａと経路Ｂの両方に設置して，電子を一つ飛ばしたとき，ほぼ100%でどちらかが必ず反応するくらいまで感度を上げておけば，それは，ほぼ確実にどちらかを通過したことを知ることの出来る装置だと言っても良いでしょう．

誤解のないように繰り返しておきますと，これは，「電子が通ったら確実に分かる」のではなく，「検出された時点でそちらを通ったことが確実になる」のです．

このような装置を使うと， MXKさんの言われる通りになることに同意します．

Re: 電子の波動性について

zoro さんのレス (2007/04/07(Sat) 09:43)

あすかさん，

私の検討は進んでいないのですが，私の意見を保留している理由は，ご紹介のあった資料の先頭部にある；・検出器の効果を見る第二段実験での「分波器」と「通過検出器Da」に納得がいかない為です．

特に「通過検出器Da」の作用をどのように考えるか判らなかったので，出典もとの本を読むか，最近の参考書を拝見してから考えようと思ったからです．

一般に，通過検出器というものは，古典的粒子の測定を考えてみても面倒な事がわかります．粒子が検出器に近づいただけでは駄目で，「通り抜けた」という事実を100%完全に測定によって証明することは出来ないように思います．

＃「通りぬける」を知るには，前後に時間差と空間の位置差が出来たことを，同時に知るという困難が起ります．＃入射側の粒子のエネルギとか，空間の制限で，ある程度問題を緩和できるとは思いますが...．

まして，考察対象が，量子力学的なミクロの対象あった場合，その通過挙動を通過検出器がマクロな通過情報として出力し，其の結果を後方におかれた検出器に，同時計測のアンチ・コインシデンスとして処理できる事を意味します．たとえ原理的にだとしても，100%の確度でこのような操作が可能とは思えません．

ご紹介のサイトが引用されているのは，岩波新書ですが，その他の参考図書をご存知でしたら，お教え願えませんか？

Re: 電子の波動性について

あすかさんのレス (2007/04/07(Sat) 10:45)

＞zoroさん申し訳ありません．他の参考資料はわかりません．見つけたら記載します．

＞ＥＭＡＮさん「検出された時点でそちらを通った事が確実になる」と言うことは，「検出されなければ50％ずつ両方の経路を通っている」という事でよろしいのでしょうか？と，言うことは，検出されない(Aを通った？)場合は Bにも検出機をつけなかった場合同様 (ψA＋ψB)の２乗ですか？それとも検出されない→Aを通った→Aに収縮→Aから電子を発射した場合と同じ現象→ ψAの２乗になるのでしょうか？

MXKさんの意見の理由は後者でよろしいですか？まだ勧められた文献を見てない状態で質問してすみません

Re: 電子の波動性について

MXK さんのレス (2007/04/07(Sat) 23:38)

はい，一方だけを見張ることも「不在の測定」として有効です．

ところで，そもそも，装置を置いただけで，干渉項が消えて， |ψA|の２乗＋|ψＢ|の２乗になるという点は大丈夫でしょうか？

Re: 電子の波動性について

ＥＭＡＮさんのレス (2007/04/07(Sat) 23:42)

後者の方で，MXKさんと同じです．

私は最初，B で検出されなければ A を通ったのだと確実に言えるのか？という点で悩みましたので，意見がふらついてしまいました．

B の感度が十分であることを，前に話した方法で予め試しておけば，「B で検出されなければ A を通った」と言えると思います．

Re: 電子の波動性について

あすかさんのレス (2007/04/08(Sun) 02:10)

ありがとうございます．

もう少しだけ質問をいいでしょうか．数式の表示の仕方がようやくわかりました(^∀^*)／

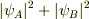$|\psi_{A}|^{2} + |\psi_{B}|^{2}$ になるというのは，実験結果でしょうか．それとも理論上の思考結果でしょうか．

B側に検出器を置かない場合は 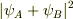$|\psi_{A} + \psi_{B}|^{2}$ になり，B側に検出器を置いた場合は 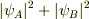$|\psi_{A}|^{2} + |\psi_{B}|^{2}$ となる要因とは，

１．「人間が認知」したからでしょうかそれとも２．検出器Bの影響（電磁波や，光学的，空間的な何か）でしょうか

１は物理学に持ち込んではいけない思想だと思っています．これが要因の場合，このスレッドは終了させて，別スレッドにてご意見を伺いたいと思います．

２の場合，検出器の影響がAに(物理的に直接)影響を及ぼしているとは考えられないため， Aを通る電子は，何かしらの手段にて B側に検出器があり，かつ，電源が入っており，かつ，十分に検出可能な能力を知っていることになります．

１，２のどちらの要因で 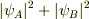$|\psi_{A}|^{2} + |\psi_{B}|^{2}$ になるのでしょうか．

最後の質問になるかもしれませんが，よろしくお願いします．

Re: 電子の波動性について

MXK さんのレス (2007/04/08(Sun) 13:41)

どうも，話を神秘的な方向に誘導されているようですが... 1でも2でもありません．干渉が消えるのは量子論に限った話ではなく，波なら一般に生じることです．スリットBで波の位相をかく乱すれば，古典的な波でも干渉縞は消えます．光の場合だと，スリットBで偏光を90度まわすような操作をしても干渉しなくなります．量子の場合は測定系との量子相関の形成が干渉消失の原因ですが，この辺りはよい教科書で勉強してください．

Re: 電子の波動性について

zoro さんのレス (2007/04/08(Sun) 19:30)

あすかさん，私は観点の違うコメントとします．

というのも，量子力学の勉強したころから40年の月日が経ち，用語すら忘れていた私が，このスレッドを拝見して，とても興味をそそられたからです．という訳で，回答するレベルにありませんが，自分で，今回気になっている事をメモしておきます．今後，ご検討される時の軽いヒント程度です．

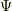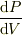
(1)波動関数 $\Psi$ と確率密度 $\frac{\mbox{d} P}{\mbox{d}V}$

今回お示しになったサイトの資料で，驚いたのは波動関数があたかも実数関数として扱われていた事です．原理的に，波動関数は虚数関数ですから，特に原理的な話の時には，面倒でも丁寧に記述する方が良いとおもいます．

いま，電子は位置の関数だけで記述されているとして；

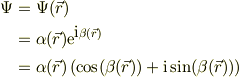
$\Psi &= \Psi(\vec r) \\&= \alpha(\vec r)\mbox{e}^{\mbox{i}\beta(\vec r)}\\&= \alpha(\vec r)\left( \cos(\beta(\vec r))+\mbox{i} \sin(\beta(\vec r))\right)$

ここで，波動関数の絶対値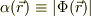， $\alpha(\vec r) \equiv |\Phi(\vec r)|$ ，波動関数の位相角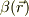， $\beta(\vec r)$

このとき，ある位置に見いだされる確率密度；

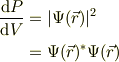
$\frac{\mbox{d} P}{\mbox{d}V}&= |\Psi(\vec r)|^2\\&= \Psi(\vec r)^{*}\Psi(\vec r)$

絶対値記号の方が簡単に書けますが，今回のようにクロス項が強く意味を持つ場合には複素共役記号の方が間違え難いと思います．また，任意の複素数について，

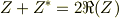
$Z + Z^{*} = 2\Re (Z)$

ですね．

電子が１スリットの量子系に入ったらどうなるのか？

電子が「ミクロの量子状態」にある限り，波動関数で記述されています．ところが其の電子に対して位置とか速度を計測する装置（今の論議での後方の検出器）と相互作用した段階で，其の波動関数は収縮すると理解しています(うろ覚え)：これをすこし説明してみましょう．

ある一つの電子を考える時に，その波動性と粒子性は「同時に共存しない」と言う点が大事だと思います．

私が学生の頃は，今回の論議での「1スリット」系の振る舞い自体が，波動的な振る舞い，中心の前方にピークがくるものの，左右に谷・山が出るのは驚きでした．きっと頭が固かったのでしょうね．

当時は，ドブロイ波と考えて，スリットの左右からの位相差を取れば，云々・・・と苦しんだのを思い出しました．学部１年の夏の頃と思いますが．

さらに，この波動性と測定された場合に，荷電粒子として計測器に掛かったばあいで，紛糾したと思います．結局，マクロな計測段階に入った電子の波動は収縮して，量子系から離れると考えていたと思います．

では２スリットが開いたらどうなるのか？

この手の問題にぶつかる頃は，量子力学は不得意ながら，シュレディンガー方程式を知りだしていたので，電磁気の得意な私としては，

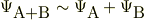
$\Psi_{\mbox{A+B}} \sim \Psi_{\mbox{A}} + \Psi_{\mbox{B}}$

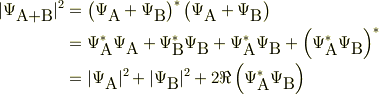
$|\Psi_{\mbox{A+B}}|^{2} &= \left(\Psi_{\mbox{A}} + \Psi_{\mbox{B}}\right)^{*}\left(\Psi_{\mbox{A}} + \Psi_{\mbox{B}}\right)\\&= \Psi_{\mbox{A}}^{*}\Psi_{\mbox{A}} + \Psi_{\mbox{B}}^{*}\Psi_{\mbox{B}} + \Psi_{\mbox{A}}^{*}\Psi_{\mbox{B}} +\left( \Psi_{\mbox{A}}^{*}\Psi_{\mbox{B}} \right)^{*}\\&= |\Psi_{\mbox{A}}|^{2} + |\Psi_{\mbox{B}}|^{2} +2\Re \left( \Psi_{\mbox{A}}^{*}\Psi_{\mbox{B}} \right)$

と言われても，波動現象についてのしごく一般的な「物理的仮定」と思ったと思います．ただ，当時は，多数回の測定も本質的だろうとおもっていました．

＃なお，完全な等号としないのは，＃スリットが新たに出来た事の摂動は含まれていない筈だからです．＃事実上は等号でも良いでしょうが，原理的には近似と考えた方が良いと思います．

ところが，こちらの掲示板に来て，以前，「２スリットに１フォトンが入射する」問題を拝見して，1フォトンと謂えども，全てのパスを反映して散乱している事に驚きました．ですから，上記の線形結合で状態が表せるというのは，量子系の本質的な性質であろうと感じています．でも，まだ納得できていないのも事実です．

そのような経緯から，私は，今回のご質問に，いまだ正攻法で回答できません．当面，時間が取れるごとに，量子力学を自分なりに見直したいと思います．そのような動機付けを戴いたことに感謝します．

Re: 電子の波動性について

あすかさんのレス (2007/04/10(Tue) 13:17)

二人の返信をじ〜っくり読ませていただきました．

混乱してました．難しいですね…

普通の波も 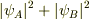$|\psi_A|^{2} + |\psi_B|^{2}$ になるんですか？波は難しいです．

でも，ここで教えて頂いたことを頭に入れながら参考書等を読むと，以前より理解できるようになりました．ありがとうございます．

Re: 電子の波動性について

zoro さんのレス (2007/04/10(Tue) 18:53)

＞普通の波も 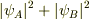$|\psi_A|^{2} + |\psi_B|^{2}$ になるんですか？

すこし誤解をされていると思いますが...．普通の波だったらこうならず，むしろ，普通に 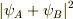$|\psi_A +\psi_B|^{2}$ となるのではないでしょうか？

量子力学の初期には，それこ観測問題について，多くの論議や実験を経て，量子状態にある粒子の波動性が検討されたのだろうと思います．お恥ずかしいことに，不勉強の結果，これらの論議を覚えていませんが．やはり，歴史的な観測問題の解説書を探して勉強されるのも一法と思います．

また，あすかさんが，ご自分で引用されたサイトの下の方に，その文献の筆者方のグループによるシミュレーション結果として書かれている「測定過程の数値実験（Ｎは検出器（候補）内の構成要素の数々，εは秩序変数の値）」の詳しい結果を追跡されたほうが，下手な解説を聴かれるより，よほど為になると感じます．

以上，じっくりとご検討されるとよいですね．

Re: 電子の波動性について

MXK さんのレス (2007/04/16(Mon) 00:25)

相対位相 $\phi$ がゆらぐと，古典的な波でも干渉項はきえます．

$\frac{1}{2\pi}\int_0^{2\pi}|\psi_{\rm A}+{\rm e}^{{\rm i}\phi}\psi_{\rm B}|^2{\rm d}\phi=|\psi_{\rm A}|^2+|\psi_{\rm B}|^2$

多分，大丈夫だと思いますが，念のため．

[home] [掲示板] [ページの先頭]