小林＠那須 さんの書込 (2007/04/01(Sun) 09:20)

皆様は SI 単位系で 1`kg を 1 とする理由をどのように説明されるでしょう か．1`sec, 1`meter を基本単位とするならば，1`g を基本単位に選択するの が単純です．1 Kg は 1000`gram であり，これを質量の単位ユニットとする のは不合理です．

皆様は 1`kg を 1 単位とするのを どのように説明されているでしょうか

zoro さんのレス (2007/04/01(Sun) 11:02)

小林＠那須さん，

私もそのように考えるのが自然だとおもいます．単位系と指数部の分離を認めておけば，「1g」でも十分だと考える為です．

世界各国の思惑の交錯する中，曲がりなりにも決めた規格に敬意は払いますが，もうすこしザックバランで明快な説明がいると思います．私は，「c(m) g s」との対比の為に「m k(g) s」としたのではなかろうかと推測しています．

話が逸れます．天文学的な計算をするときに気が付いたのですが，距離については；

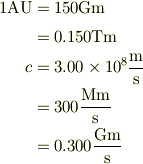
とか結構うまく表記できます．ところが，質量となると，木星の第一衛星イオについてさえ，

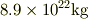
となってしまいます．其の為に，SI系は,天文学的質量の表記に目を瞑ったのではないでしょうかと推測します． 恐らく，太陽とか地球の質量を単位にして表現するのではないでしょうか？

なお，自分は，天文学的な質量を自分の報告書に書く機会がありません．物理・化学の関係で書く時は，ng, ug, mg, g, kg, を適宜，使っています．

小林＠那須 さんのレス (2007/04/01(Sun) 12:57)

私は SI 単位系は `ampere と `volt 単位に妥協した単位系だと考えています． `volt と `ampere の単位を使い続けるために，他の基本単位をどうするかの 妥協案として出来上がった単位系だったと考えます．妥協の結果として 1`kg を基本単位に選択したのだと考えます．

1 watt == 1 `volt * 1`amper == 1`joule/`sec == 1`newton `meter/`sec

== 1 `kg `meter/`sec^2 `meter/`sec == 1 `kg `meter^2/`sec^3

上の関係式で 1 watt == 1 `vold `ampere の電磁エネルギーの単位を，ニュー トン力学での質量と`meter `sec の基本単位の組み合わせで表現するとき， 上のように質量の基本単位を `kg に選択せざるをえなかったのだと思います． 長さや時間の単位の側で調整しようにも，べき乗が入り込んでいるきて嫌ら しいくなりすぎます．

上の経緯が明確に書かれた文献を見たことがありません．でも SI 単位系， 特に その電磁単位系を冷静に見直してみれば間違いないと思います．私は SI 電磁単位系が複雑すぎて誰も書かないのだと思っています．

zoro さんのレス (2007/04/01(Sun) 13:23)

＞私は SI 単位系は `ampere と `volt 単位に妥協した単位系だと考えています．

私も，これはそうだろうと思います．

＞べき乗が入り込んでいるきて嫌らしいくなりすぎます．

でも，其の為に接頭語「k」が導入されているのですから，質量の基本単位は「kg」でなくて「g」であり，「N」とか「W」の定義にでてくる質量に「kg」を用いるのはかまわないのではないでしょうか？

＞ SI 電磁単位系が複雑すぎて

というのは，どんな点でしょうか？

小林＠那須 さんのレス (2007/04/01(Sun) 14:34)

この投稿には，下の「解りにくい MKSA 単位系となった経緯」を より解りや すく書き直す方向を探る目的もあります．

• http://www.nasuinfo.or.jp/FreeSpace/kenji/sf/ElMgUnit.html

私は SI 単位系における電磁気学の単位系は非常に捻くれた単位系だと主張 します．電磁気学を学ぶためには夾雑物が入り込みすぎて不適切だと考えま す．もちろん SI 単位系を定めた委員たちが このような単位系を選択せざる を得なかった歴史的背景も理解できます．当時 `ampare や `volt を使わな い新しい合理的な単位系を作ったとしても誰も使わなかったと思います．実 際 SI 電磁単位系のつじつま合わせとして導入された磁荷の単位 weber の浸 透は遅いままです．未だもって磁束密度:gauss のほうに馴染んでいる方のほ うが多数派です．

逆に `ampere や `volt に馴染みすぎてしまっているため，私が 「SI 単位 系の電磁単位系は捻くれる過ぎていて理解するのが非常に難しい」と言って も，なかなか通じません．「何を変なことを言っている」「とんでもか」と 思われてしまうことも多くあります．

皆様には先の「 `volt, `ampere があったから，SI 単位系では 1`kg を基本 単位にせざるをえなかった」との説明で納得してもらえますでしょうか．

>＞ SI 電磁単位系が複雑すぎて >というのは，どんな点でしょうか？

物理学科の卒業生でありながら， 1`colomb の電荷どうしを 1`meter の距離 だけ離したときの力は < 8.98755e+009 > `newton という凄まじい力である ことを知らな馬鹿がいます．(私のことです．でも私だけでは有りません．) これは電流 `ampere の基本単位の定義から `ε0, `μ0 の値と単位次元を誘 導できていないからです．物理学科の人間でも「電流定義から `ε0, `μ0 の値と単位次元が導出する過程を説明せよ」と問題を出したとき何パーセン トが答えられるでしょうか．

また `weber なんて誘導単位を基本単位から導出できる者がどれ位いるでし ょうか？物理学科の学生でも殆どが導出できないと思います．私が先の web page を書いたのは，これが自分で解らなくて，また納得できる説明が無 くて不満だったからです．やっと解ったことをまとめてみたのですが，自分 でも下手な説明しかできていないと感じます．でも説明が難しいから誰も書 かないのだとも思います．

こんな捻くれた単位系を「複雑すぎ」と評しても許されるでしょう．

MXK さんのレス (2007/04/07(Sat) 23:42)

1クーロンの電荷同士に働く力が大きいのは，単位系の問題というより， 磁気の力が一般的な状況では電気力に比べて非常に小さいことにあります． 電荷の単位を小さくとれば，今度は電流による力がとても小さくなって しまいます．

1グラム，あるいは１キログラムの質点同士を1メートルの距離に置いたときの 重力を計算してみたらどうでしょう？ この小ささも，どこか単位系がおかしいからでしょうか？

小林＠那須 さんのレス (2007/04/09(Mon) 07:45)

>磁気の力が一般的な状況では電気力に比べて非常に小さい

同意します．私の言葉で言い直すと，3e+8 `meter/`sec という大きな光速度 定数が入り込んでくるためです．

>この小ささも，どこか単位系がおかしいからでしょうか？

違います．極端に大きな数や小さな数が入り込んでも複雑にはなりません． 現在は平気で `G `Hz, `n `meter などの言葉が新聞で書かれる時代です．歴 史的にも ampere, volt はこの桁数の別名でした．emu 単位系でのユニット 電流の 10^-1 の意味で ampere が使われ，emu 単位電圧の 10^8 の意味で volt が使われていました．私が おかしいと主張したのは，物理学科の卒業 生でさえ 1`meter 1`coulomb の電荷どうしに働く力が 90 億ニュートンであ ると知らないことです．自分の五官の感覚と結びつけて理解することを難し くしている電磁気学の教科書です．その難しさの理由が SI 電磁単位系です．

私は，SI 単位系を複雑にしているのは ε0 μ0 という物理的に必然性のな い定数を導入したことだと考えます．それに人間の都合で単位次元さえ持た せててしまったことが SI 電磁単位系の理解を困難にしています．これによ り基本単位から誘導単位を順次導入していく電磁気学の教科書を書けなくし ています．weber の誘導単位を `ampere 基本単位から誘導できる方は物理学 科の卒業生でも殆どいないと思います．ε0 μ0 には `coulomb/(`volt `meter), `weber/(`ampere `meter) の単位次元が人間の都合で導入されまし た．この ε0， μ0 の単位次元が定まる理由を説明できる方は殆どいないで しょう．私は その説明を見たことがありません．電磁気学を学ぶためには真 空の誘電率・透磁率は単位次元を持たない 1 としておくほうが話を単純にで きます．実際 Gauss 単位系では そうなります．

私は SI 単位系は歴史の経緯により解り難い単位系になっていると主張しま す．その単純な例が，掲題の 1`kg を質量の単位ユニットにしたことです． キロの桁数表記を使いながら 1`kg を 質量単位ユニットの1000倍にできなか ったことです．MXK さんには，No.15156 で書いた 1`kg をユニット単位にす る理由の説明で納得できますでしょうか．

小林＠那須 さんのレス (2007/04/11(Wed) 05:20)

>emu 単位系でのユニット電流の 10^-1 の意味で ampere が使われ，emu 単位 >電圧の 10^8 の意味で volt が使われていました．

すいません，間違えました．逆でした．emu 単位電流の 10^-1 が ampere で あり，emu 単位電圧の 10^8 が volt です．この経緯が英文ですが下で書か れています．参考にしてください．

• http://alpha.montclair.edu/~kowalskiL/SI/SI_PAGE.HTML

ｋｏｍａｇａｔａｋｅ さんのレス (2007/04/11(Wed) 10:25)

話が難しくて付いていけないのですが． ボルトとクーロンのイメージの部分についてだけ書かせて頂きます．

＞歴史的にも ampere, volt はこの桁数の別名でした．emu 単位系でのユニット 電流の 10^-1 の意味で ampere が使われ，emu 単位電圧の 10^8 の意味で volt が使われていました．

これは本当でしょうか．

電圧単位のｖｏｌｔは電池を初めて作ったボルタの名前に由来するというのはたいていの本に載っていますのでよく知られていることです．でも名前だけのことだと思っている人が多いようです．１Ｖという大きさ自体もボルタ電池に由来するという風に考えている人は少ないのではないのでしょうか．皆さんはどうでしょうか．

ボルタ電池は起電力が安定していませんでした．ダニエル電池で初めて実用的になりました．私が作ったものではボルタ電池でソーラーモータを回すと数分で出力が落ちてしまいます．ダニエル電池では数時間回り続けます．電極は同じですが溶液の種類と構造をかえるとこれだけ変わってきます． このダニエル電池を直列にすれば電圧を増やしていくことが出来ます．ダニエル電池１個分，２個分，・・・となります．１Ｄ，２Ｄ，・・・と呼べばよかったと思うのですが当時（ごく最近まで）ダニエル電池はボルタ電池の改良版と理解されていましたので１Ｖ，２Ｖ，・・・となりました．ダニエル電池の理論起電力は１．１Ｖです．銅と亜鉛の酸化・還元電位から求めることが出来ます．ダニエル電池１個分の起電力が１Ｖの基準だと言ってよいと思います．オームがオームの法則を調べたのもこのダニエル電池だと思います． 注ダニエル電池とボルタ電池は反応物質，反応機構が異なりますので別のものです．ずっと極板が電池の主役であると誤解されていました．同じ極板が使われているので同じだと扱われていたのです．いまでもそう思っている人とが多いです．ＴＶでの説明もほとんどがそうです．以前は教科書の記述もそのようになっていました．

ｅｍｕから１０＾８で変換してＶを出すのが歴史的な由来だというのはちょっと「？」を感じます．

＞私が おかしいと主張したのは，物理学科の卒業生でさえ 1`meter 1`coulomb の電荷どうしに働く力が 90 億ニュートンであると知らないことです．自分の五官の感覚と結びつけて理解することを難しくしている電磁気学の教科書です．その難しさの理由が SI 電磁単位系です．

イメージの食い違いは色々あります．

１クーロンという値がとんでもなく大きなものであるということがピンと来ない理由は別にあると思います． 乾電池で豆球を点灯したときにも１Ａ前後の電流は流れます．１Ａで１秒間，０．１Ａでだと１０秒間流れたときに１クーロンの電気量が移動するということの方が馴染みがあるのです．これがとんでもない値であるとイメージできる人はいないと思います．クーロンの法則の式を習って，値を当たってみて初めて分かることなのです．でも数字として分かっても量として実感できないという場合が多いです．昔はｅｍｕ単位でした．そこから力をｄｙｎｅに直して見ていました．元々のｅｍｕ単位がＶ，Ａ，Ｃと違うのですから何のことかピンと来ません．クーロンから力をＮで出した値を見て初めて分かることです．恥ずかしながら私は高校の教科書を教える立場で見るまでは分かりませんでした．それまではｅｍｕ，ｄｙｎｅでした．クーロンの引力の式が簡単になるということだけで値としての実感は取りようがありませんでした． １クーロンがとんでもない大きさだということはコンデンサーの容量に何故あれだけ小さな単位が出てくるかとつながっているのですがこれのわかっている人もまた少ないでしょう．なぜｐ（ピコ）Ｆという小さな値が出てくるかが分からなかったのです．

電磁気学の入門書で上の２つのクーロンのイメージの食い違いを説明しているのを見たことがありません．そもそもイメージが食い違っているということ自体意識されていないのです．

電気分解で出てくる電気等量（電子１モルに相当する電気量）の値は９６５００クーロンです．化学で入試を受けた大学生ならまだ覚えているかもしれない値です．でもこれがとんでもない値であるとは誰も思っていないでしょう． 電解精錬で銅３２ｇを取り出す電気量です．銅３２ｇなんてわずかな量です．皆多分「たいしたことはない値だ」と受け止めていると思います．電線の銅は全て電気銅であるということからすると９６５００クーロンにビックリする方がおかしいかもしれません． 水の電気分解で泡が発生したとします．ぼこぼこと泡が見えたらもう数クーロンの電気が移動しているのですからこれも大した電気量ではないと考えるでしょう．水の電気分解なんて小学校でやることです．

イメージの食い違いの理由は単位系とは別のものではないでしょうか．

上で挙げたイメージの食い違いの理由の一つは静電気と動電気によるものです． 私はバケツリレーで運んだ水とその結果たまった水との違いで説明しました．たまった水とリレーで運んだ水の量は同じです．でもたまった水を持つことはもう出来ません．

１Ｖという電位の大きさもエネルギーとして実感するのが難しいです． 電圧の１Ｖはそれほど大きい値だとは思われていないのが普通です．でもその１Ｖで電子を加速したときのエネルギー１ｅＶはとんでもなく大きな値です．イメージが食い違います．化学反応のエネルギーがｅＶのレベルであるということと電池の起電力が１Ｖの近辺にあるということはつながっています．電池の中での化学反応のエネルギーレベルもｅＶであるということです．それが外にＶとして現れてきています．

１ｅＶは１万度と聞いて乾電池の１．５Ｖとつながる大学生は少ないと思います．

zoro さんのレス (2007/04/11(Wed) 20:35)

＞電圧単位のｖｏｌｔは電池を初めて作ったボルタの名前に由来するというのはたいていの本に載っていますのでよく知られていることです．でも名前だけのことだと思っている人が多いようです．１Ｖという大きさ自体もボルタ電池に由来するという風に考えている人は少ないのではないのでしょうか．皆さんはどうでしょうか．

ズバリご指摘を受けた一人です．でも，今回の論議を拝見していて，電池の起電力は「 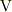」のオーダですし，何となく電気化学的な経緯が入っていると推測していました．それは，以前この掲示板で「電気抵抗を考える」といったスレッドで，ダニエル電池が出来てから，電気抵抗が正確に知られるようになった，と言った記事があった事を思い出したからです．

私は，40年ほど前に，学部生でした．入学後すぐに，電磁気の本をそろえた所，たしかガウス単位系の本の為に，力やエネルギを出そうとすると，とても混乱したのを思い出します．また，光速がやたらと方程式に出て来て，とても不自然な印象をお持ちましたので，その本はお蔵入りにしました．

でも，電磁単位系(cgs-emu)の電位差，起電力の単位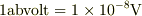， を使えば，最近の乾電池の起電力は；

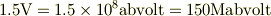
とかになるだけで，日常感覚と乖離するとも思いません．むしろドル・円の換算みたいに見えるだけではないでしょうか．極論する限り，十の冪は，慣れてしまえば，皆同じ，とか．

＞１ｅＶは１万度と聞いて

という見方は初めて拝見しました．ディスプレイの色温度を5500Kと低めの設定をしているので，その2倍の温度なんですね．

私の場合は，逆に室温でのエネルギをeVに換算していました．

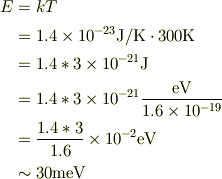
ここで

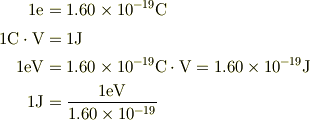
やはり，MKSAの醍醐味は，力学量が簡単に出てくるので，記憶の負担が少ない事ではないでしょうか．また，光速が電場・磁場の波動方程式になって，こつ然と表舞台に出てくるのは，歌舞伎のどんでん返しを彷彿として，嬉しく感じました．

結局，私は，MKSAを「MGSA」にしてくれるなら，SI単位系には妥協できるタイプのようです(笑)．

小林＠那須 さんのレス (2007/04/12(Thu) 08:47)

御指摘ありがとうございます．

>＞歴史的にも ampere, volt はこの桁数の別名でした．emu 単位系でのユニット >>電流の 10^-1 の意味で ampere が使われ，emu 単位電圧の 10^8 の意味で >>volt が使われていました．

>これは本当でしょうか．

自分の説明の都合を優先して単純化しすぎました．詳しく書いてみます．で も どうしても面倒な説明になってしまいます．

1863 年に emu 単位系が Maxwell を中心に定められました．単位電流を 1`cm 話した二本の直線電流に流したとき 2`dyne の力が働くことから定めま した．emu 単位系は光速度定数を含む Maxwell 方程式を前提とした奇麗な理 論体系を持つ単位系でした．しかし光速度が入り込むため，電流は良くても 抵抗や電圧は標準抵抗や標準電池とは 10^8 -- 10^9 も大きな値となりまし た．しかも，このような電流定義では基準となる単位電流を実験室で実現す るのが困難です．結果として広く使われるには至りませんでした．理論分野 で，emu 単位系の単位電流/単位電圧/単位抵抗/ は absolute ampere/aobsolute volt/absolute ohm と区別されて使われました．

そのため 1884 年から実用的な International System of Electrical and Magnetic Units が構築されていきました．単位抵抗を 1`cm^2 106`cm の水 銀の抵抗で定義しました．単位電流(以下 international ampere)を銀の電気 精錬で定めました．1 秒間に 0.00118`gram の銀を析出する電流を単位電流 と定義しました．この二つを基本単位にすれば，他の電磁単位は誘導できま す．単位電圧は単位抵抗に単位電流を流すことで定まります． International Sytem Of Electrical and Magnetic の単位抵抗，単位電圧は， 既に存在していた標準電池や標準抵抗とも近い値でした．理論的に明晰な emu 単位系とは電流で 10^-1 倍だけ異なるるように，電圧で 10^8 倍だけ異 なるように定められました．

1948 年に SI 電磁単位系を定めるとき，この International ampere と `volt を使いつづけることを選択しました．というより既に広く使われてい る電流や電圧の単位を変えられなかったのが現実です．ただし単位電流は emu での電流定義を流用しました．

この経緯が下に書かれています． History of the ampere;; http://www.sizes.com/units/ampHist.htm International System of Electrical and Magnetic Units;; http://www.sizes.com/units/int_ENMsys.htm

ちなみに SI 単位系の単位電流の定義に出てくる 2e-7`newton は上の経緯 から導かれています．1`meter 離れた二本の直線電流に 1`meter あたり 2e-7 `newton の力働く電流は，2`dyne == 2e-5 `newton に (10^-1)^2 を 掛けた数値として導入されました．10^-1 は international ampere が absolute ampere の 10^-1 であったことから来ています．二本の平行直線電 流に働く力は I^2/r に比例することより，1/10 の自乗が 1e-5 `newton に 掛かります．

SI 単位系は電流定義に emu の考え方を使いましたが，internatinal ampere, volt に妥協するため，物理的に必然性のない μ0, ε0 の比例定数 を導入しました．しかも この定数には物理的に必然性のない単位次元まで導 入してしまいました．10^8 と大きな値となる absolute volt ではなく，広 く使われるいる volt を使いつづけるため， ε0 に coulomb/(volt meter) の単位次元を与えてしまいました．この意味で MKSA 単位系は MKS `ampere `volt 単位系と言うべきです．`volt を隠してしまっては，単位系 の構成が解らなくなってしまいます．基本単位から誘導単位を導けなくなっ てしまいます．例えば `gram ではなく `kg を質量の単位ユニットにとしな ければならない必然性が解らなくなってしまいます．

>結局，私は，MKSAを「MGSA」にしてくれるなら，SI単位系には妥協できるタイプのようです(笑)．

もう少し複雑です．M gram S ampere 単位系とするためには M gram S amper milli-volt 単位系にせねばなりません．そうしないと 電荷*電圧 C*V と M gram S で表したエネルギーの間に比例係数が必要になってしまい ます．zoro さんが Gauss 単位系で味わった嫌らしさが出てきてしまいます． この意味で SI 単位系を MKS `ampere `volt 単位系と理解しておく必要があ ります．

MXK さんのレス (2007/04/12(Thu) 11:30)

アンペア × ボルト ＝ ワット で力学的な量になるので，電磁的な単位としては，どちらか を基本単位とすれば十分だと思います．MKSA, MKSVのどちらでもいいわけです．歴史的には MKSΩを考えていた時期もあるようです．

キログラムのキロについては，今問題にされている電磁単位系(MKSA)ではなく， 力学的な単位系(MKS)の問題だと思います． Wikipedia(英語版) によれば， 当初 1キログラムに相当する 1グラーブという単位が準備されていたが， フランス革命によって，爵位を意味する言葉は不適切(politically incorrect)ということで， 急遽キログラムになったという経緯が書いてあります．なんと政治的理由なのですね． もう少し早い時期にMKS単位系が確定していれば，キロなしで済んだのかもしれません． いずれにせよ，電磁的な単位系が議論されるよりずっと前の時代のことです．

小林＠那須 さんのレス (2007/04/13(Fri) 07:52)

MXK さん，レスありがとうございます．

>キログラムのキロについては，今問題にされている電磁単位系(MKSA)ではなく， >力学的な単位系(MKS)の問題だと思います．

meter と sec と `gram の範囲内だけで決めるならば，1`gram を単位ユニッ トに選択するのが合理的です．でも SI 単位系の作成者たちは 1`kg を単位 ユニットに選択しました．何か理由があるはずです．

私は `volt * `ampere == watt == `joule/`sec == `kg `meter^2/`sec^3 と できるように 1`kg を選択せざるを得なかったのだと何度も主張しています． `これが納得できない理由を聞かせてもらえないでしょうか．

MXK さんのレス (2007/04/13(Fri) 16:43)

MKSの原型であるメートル法の発案が18世紀末， SIは1950年代（その原型までさかのぼっても20世紀初頭）ですから， SIを決めるに際しては，既存の力学単位系を拡張する以外の 道はなかったのだと思います．電磁気の都合で力学の単位， それも基本単位を変えるなどということは論外だったに ちがいありません．

まともな力学単位系としては MKS と cgs しかなかったので， 国際的な標準としての整備と普及の進んでいた前者を採ったのは， きわめて当然のことだと思います． （もし，仮に cgs を採用していたとしても，基本単位にセンチと という接頭語がついていたことになります．）

「なぜ MKS 単位系で 1キログラムを基本単位としたのか」という 問なら分かりますが， 「なぜ SI 単位系で 1キログラムをユニット単位とするのか」は かなり的外れな感じがします．

小林＠那須さんの記事を拝見していると，アンペアとボルトを 独立に定めることができるという印象を受けますが，

1. 力学的な基本単位とその大きさはすでに確定している． メートル，キログラム，秒 2. したがって，力学的な誘導単位の大きさもすべて決まっている． ワット，ジュール，ニュートン，...

という前提に立つと，電磁的な単位として，アンペアとボルトの大きさを 独立に決めることはできません．アンペア×ボルト＝ワットだからです． ですから，ボルトとアンペアはどちらかの大きさを決めると 他方は自動的に決まってしまいます．

実際にはSI以前の実用単位の段階でアンペアとボルトはたまたま(?) その積がワットになるように，定められていたので，気づきにくいことですが， 論理的には上のように考えるべきだと思います．

もし，そのようになっていなかった場合には，例えばアンペアとワット （つまりキログラム）を温存して，ボルトの大きさを変えざるを 得なかったと思います．

小林＠那須 さんのレス (2007/04/13(Fri) 22:05)

>実際にはSI以前の実用単位の段階でアンペアとボルトはたまたま(?) >その積がワットになるように，定められていたので

私も以前は watt と `joule/`sec と「たまたま」一致していたと思っていま した．でも逆だ watt==`kg `meter^2/`sec^3 とするため `kg を選択したの だ．そうすれば納得できる・辻褄が合うと考え直したので今回の投稿をして みました．

>まともな力学単位系としては MKS と cgs しかなかったので

MKSA 単位系の前にあったのは Internatinal System です．そして Internatinal System は cgs です． MKS はなかったはずです．MKS が両立 していたとする根拠は？

ちなみに http://www.sizes.com/units/int_ENMsys.htm で下のように書かれています． The absolute units on which the International System was based are those of the cgs electromagnetic system.

>小林＠那須さんの記事を拝見していると，アンペアとボルトを >独立に定めることができるという印象を受けますが，

誤解です．私は光速度 `c と `ampere と `volt の三つの内から二つを基準 として選択できると主張します．emu 単位系は `c と absolute ampere を基 準に定めた単位系です． MKSA 単位系は `ampere と `volt を選択しました． この二つは，時刻と長さの時と同様に，`c で結び付けられます．(length = `c time ほどに単純ではありませんが）

ちなみに下のように電磁気の単位次元を MKSA 四つで【抵抗ならば m Kg s^-3 a^-2など】と表してあることが多くあります．，これは物理的に無意味 です．抵抗は `volt/`ampere の物理次元と考えるべきです．この認識でなけ れば回路設計できません．

電気抵抗:オーム:Ω,`volt/`ampere,m Kg s^-3 A^-2

そして，この意味で電磁気の基本単位として `ampere と `volt の二つが必 要となります．MKSA 単位系では `volt は電流と同様に基本単位です．誘導 単位ではありません．

>電磁的な単位として，アンペアとボルトの大きさを >独立に決めることはできません．アンペア×ボルト＝ワットだからです．

この話の展開の仕方からすると MKK さんは ε0 の単位次元が `coulomb/(`volt `meter) であることを導けないはずだと思います．ε0 の 単位次元は人間の都合で人為的に決められたものです．物理的・自然科学的 な必然性からではありません． MKK さんは電流の定義から循環論法に陥るこ となく `ε0 の単位次元を誘導できますか？

私が SI 単位系が MKS `ampere `volt 単位系だとするのは，歴史的な経緯の 他に， `ε0, `μ0 の単位次元の説明を付けるられるからです．

MXK さんのレス (2007/04/13(Fri) 23:17)

MKS単位系については "MKS unit" ぐらいのキーワードで 検索してください．

電磁的な単位系に囚われすぎているように思います． 当初は電流や電圧は勝手に決められていましたが， 次第に力学的量との比較で定義されるようになりました． その結果, esu, emu, gauss では電磁気的基本単位の数が ０に，MKSAでは１個にまで減ったわけです．

繰り返しになりますが，ワットやジュールは電磁気とは独立に 力学的に定義された量です．

力学的エネルギーと電磁気学的エネルギーの等価性を利用して， それらを電磁気にも転用していると考えることができます． ですから，アンペアを決めると，ボルトは自動的に決まって しまいます．

> MKSA 単位系では `volt は電流と同様に基本単位です．誘導
> 単位ではありません．

そんなことは，どこにも書いてありません．ぜひ，SIの文書

• http://www.bipm.org/utils/common/pdf/si_brochure_8_en.pdf

を読んでください． まちがった理解に基づいて批判すると，無用の混乱を招くだけです．

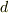隔たった平行な電線に 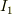, 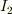の電流が流れているときに，長さ の部分に働く力は 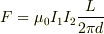なので

つまり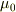， の次元あるいは単位は

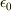です． の次元は 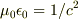から 求まります．もちろんクーロンの法則から上と同じように出すことも できるでしょう．

小林＠那須 さんのレス (2007/04/14(Sat) 00:43)

>MKS単位系については "MKS unit" ぐらいのキーワードで >検索してください．

だめです．SI 単位系について引っかかるばかりです．SI 単位系が定まるよ り前に MKS 単位系が広く使われているとされるものはあったとしても埋もれ てしまいます．

cgs が広く使われていたことは emu 単位系の話や 1cm^3 の水が 1g である ことなどからも納得できます．それに比較して MKS にする必然性がないと思 います．MKS にするぐらいなら M `gram S にするでしょう．

具体的な URL で示してもらえますでしょうか．

F = μ0 I1 I2 /( 2 π d)

から μ0 の単位次元を `kg `meter/(`ampere^2 `sec^2) とするのは循環論 法です．二本の直線電流に働く力から単位電流を決めるときの μ0=2e-7 の マジックナンバーは emu の時と同様に無次元の定数でなければなりません． ここで `ampere の次元を含ませてしまっては循環論法です．emu の単位次元 のときと同様に μ0 は無次元とし I の次元を {F d]^(1/2) = (`kg `meter^2/`sec^2)^(1/2) としておくべきでしょう．真空の透磁率は 1 のま まにしておくべきでしょう．

また SI 単位系での透磁率は `weber/(`ampere `meter) = `volt `sec/(`ampere `meter) の単位次元です．`kg `meter `kg `sec^-2 `qmpere^-2 には物理的意味はありません．先に書いた抵抗の単位次元を `meter `kg s^-3 A^-2 とする誤りです．抵抗の単位次元は `volt/`ampere です．

もちろん私だけが MKS `ampere `volt 単位系だと言っており，他に書かれて いないことは承知しています．でも抵抗の単位は `volt/`ampere です．抵抗 の単位次元を`meter `kg s^-3 A^-2 と認識して回路設計者はいません．これ は SI 単位系が定まる以前からの回路設計者の共通認識です．実際 SI 単位 系が定まる以前から `volt と `ampere 使われていました．だからこそ SI 単位系の作成者たちは 旧来の `volt と `ampere を使い続けざるを得なかっ たわけです．この `ampere と `volt に妥協したことから ε0 と μ0 の単 位次元が導入されています．MXK さんの導入の仕方では，SI 単位系が定まる 以前の `volt と `ampere の存在を無視しています．回路設計者にとって抵 抗が `volt/`amper の次元であったこと(現在でも)を無視しています．

まったく新規に単位系を定めるのだったら，相対論の <φ, A>:電位とベクト ル・ポテンシャルの四元ベクトルを元に電磁単位系を定義し直したと思いま す．その方が合理的で直感的な単位系にできます．そして物理的必然性のな い ε0 や μ0 などは導入しなかったでしょう．1948 年当時の物理の専門家 ならば，そのような単位系にしたはずです．MXK さんも同様に考えませんか？

>そんなことは，どこにも書いてありません．ぜひ，SIの文書 > http://www.bipm.org/utils/common/pdf/si_brochure_8_en.pdf

こちらは知りませんでした．有難うございます．腰を落ち着けて読んでみます．

小林＠那須 さんのレス (2007/04/14(Sat) 02:51)

>そんなことは，どこにも書いてありません．ぜひ，SIの文書 > http://www.bipm.org/utils/common/pdf/si_brochure_8_en.pdf

飛ばし読みですが電磁気の単位に関連しそうなところを見てみました．この 文章は Candera なども含めた SI 単位系一般の広範な説明です．電磁単位系 を決めた経緯，背景にある考え方までには踏み込んでいないと読めます． MXK さんは，この文章のどこを読むべきと考えているのか具体的に指摘願え ないでしょうか

MXK さんのレス (2007/04/14(Sat) 12:07)

単位系のことを議論しているのに，"MKS単位系" をご存じないというのは ちょっと驚きです．

>>MKS単位系については "MKS unit" ぐらいのキーワードで >>検索してください．

> だめです．SI 単位系について引っかかるばかりです．SI 単位系が定まるよ
> り前に MKS 単位系が広く使われているとされるものはあったとしても埋もれ
> てしまいます．

不思議ですね．何かフィルタでもかかっているのでしょうか． わたしのところは，

• http://www.unc.edu/~rowlett/units/cgsmks.html

を筆頭に541,000件にヒットしますけどね．

"MKS unit french-revolution","MKS MKSA" とかでもいいと 思いますが．

> cgs が広く使われていたことは emu 単位系の話や 1cm^3 の水が 1g である
> ことなどからも納得できます．それに比較して MKS にする必然性がないと思
> います．MKS にするぐらいなら M `gram S にするでしょう． ::

> 具体的な URL で示してもらえますでしょうか．

以前(No.15282)，ご紹介した，

• http://en.wikipedia.org/wiki/Kilogram

も読んでおられないようなので，URLを書いておきます．

> また SI 単位系での透磁率は `weber/(`ampere `meter) = `volt
> `sec/(`ampere `meter) の単位次元です．
> `kg `meter `kg `sec^-2
> `ampere^-2 には物理的意味はありません．

物理的意味がないとされる根拠は何でしょうか．

>  先に書いた抵抗の単位次元を
> `meter `kg s^-3 A^-2 とする誤りです．抵抗の単位次元は `volt/`ampere
> です．

ここで認識が完全に誤っています．ここの誤解が 「私だけが MKS `ampere `volt 単位系だと言っており，他に書かれて いない」という事態に至っている理由です．

例えば，WIkipediaのボルトの項

• http://en.wikipedia.org/wiki/Volt

にある，

The volt (symbol: V) is the SI "derived" unit of electric potential difference or electromotive force.

The volt is defined as the potential difference across a conductor when a current of one ampere dissipates "one watt" of power.

が理解できない，あるいは根拠なく間違いだと断定されるのであれば， これ以上議論しても無駄だと思います．

小林＠那須さんは，ボルトは誘導単位ではなく基本単位とすべきだと主張されているの ですが，その場合，1ボルトの大きさはどのように決められるのでしょうか． 基本単位はその大きさを実際に作ってみせる方法を示す必要があります．

先に示した SI文書を先入観を完全に排除して，力学的単位にも注意を 払いながら，（1章, 2章だけでも）熟読されることを強くお勧めします．

また同じ名前の単位でも，その定義，大きさ，種別(基本単位か誘導単位か)など は，単位系や時代によって変化しているので注意が必要です．

無理解や曲解に基づいて，SIを「捻くれている」と評するのはどうかと思います．

zoro さんのレス (2007/04/15(Sun) 00:21)

私は，電磁気学での単位系の変換は難しすぎて，MKSA単位系だけで考えてきました．しかし，質量の基本単位に「g」が使われていないのに，以前から不満で，今回の論議を興味深く拝見しています．

そこで，幾つかの論議で，出て来るサイトをフォローしているうちに，歴史的な問題点として捉えるよりも，「電磁気学の表現問題」と考えたらどうなるかと思って，検索をしておりました．その中で，下記のサイトに出会いました．

このサイトは，日本語で書かれていて，その中に「単位系」の考察が在ります．特に学生さんの中には，MKSA単位系だけで講義を受けており，今回の論議について行かれない方も多いのではないかと思い，下記の紹介をさせていただきます．

＝＝＝＝紹介＝＝＝＝

放送大学教授の岡部 洋一さんの「電磁気学」というサイト

• http://www.moge.org/okabe/temp/elemag/temp.html

のなかで，「単位系について」という項があり，複数の単位系； ・SI単位系としての (MKSA units) ・CGS単位系：電磁単位系(electromagnetic units，略記：cgs-emu units) ・CGS単位系：静電単位系(electrostatic units，略記：cgs-esu units) ・ガウス単位系，(Gauss units) ・ヘビサイト-ローレンツ単位系，(Heviside-Lorentz units, 略記：Heviside units)

を対象として,それぞれのマクスウェル方程式に「量方程式」という考え方を導入し，単位系ごとに設定した係数によって，相互関係を明示して行くという手段をとっています．

詳しくは，

• http://www.moge.org/okabe/temp/elemag/node84.html

をご覧下さい．

＝＝＝＝ 以上．

小林＠那須 さんのレス (2007/04/15(Sun) 06:18)

MXK さん，色々と御指摘くださりありがとうございました．おかげで何とか 頭の中を整理できました．それを書いてみます．MXK さんにも納得してもら えると思います．

なお私は自分が正しいと屁理屈を捏ね回す気はありません．電磁気学を納得 できる形で理解したいだけです．MXK さんの主張も正しいと思っています． それを前提に，前回の私の主張を修正して整理し述べ直します．

Meanwhile, the further development of the metric system was based on meter and kilogram standards created and distributed in 1889 by the International Bureau of Weights and Measures (BIPM). <==;; http://www.unc.edu/~rowlett/units/cgsmks.html

と書いてあります．1889 年から MKS 単位系も使われるようになったようで す．知りませんでした．

でも既に使われていた CGS 単位系があるにもかかわらず MKS 単位系を使う ようになったのは理由があるはずです．M `gram S 単位系ではなく M `kg S にする必然性があったはずです．「grave 単位を使おうとした」では弱す ぎます．

その理由として `ampere * `volt == watt と `newton `meter `sec^-2 を 同じ：== として扱いたいとする産業界からの要望があったとすれば納得でき ます．1863 年に emu 単位系ができたときから practical units として `ampere, `volt が使われていました．また 1882 年にエジソンの電力システ ムが稼動を始めました．ですから 1880 年代に `ampere*`volt == watt を使 った設計作業が多くなされるようになっはずです．その過程で cgs ではなく 比例係数を省略できる MKS が使われるようになったのだろうと推測します．

小林＠那須 さんのレス (2007/04/15(Sun) 06:20)

電磁気学の記述には二つの基本量が必要です．電界の世界での基本電荷と磁 界の世界での基本磁荷で構成されるのが Gass 単位系です．回路設計の世界 では `ampere, `volt, の二つが基本単位とされます．この二つから `ohm = `volt/`ampere などと他の電磁単位が誘導されます．emu 単位系のように 光速度の普遍性から基本単位を一つにすることも可能です．でも逆に解り難 くなると思います．

> MKSA 単位系では `volt は電流と同様に基本単位です．誘導
> 単位ではありません．

は言いすぎでした．言い直します．「 MKSA 単位系でも `volt を電流と同様 な基本単位と捉えるべきです．誘導単位と捉えるべきではありません． MKSA 単位系では `ampere*`volt == `joule/`sec の関係から `joule/`ampere によって導かれる誘導単位にされてしまっています．でもこ れは形式的な話であり実体は逆です．MKSA 単位系は電磁気の基本量から表さ れるエネルギーと，質量・時間・長さの基本量から表されるエネルギーを変 換係数なしで == で結び付けられるような単位系を選択しました．その結果 として `volt = `joule/(`sec `ampere) と `volt が誘導単位になったと理 解すべきです．」と修正します．

MKSA 単位系の名称から，単位を MKSA の四つだけで表そうとしますが，それ は誤りです．`volt も基本単位に加えて理解すべきです．形式的に抵抗の単 位次元を `meter `kg s^-3 A^-2 とすることもできます．でも抵抗の単位次 元は `volt/`ampere と捉えるべきです．1 `ohmの抵抗は「 1 `volt の電圧 を掛けたとき 1`ampere の電流が流れる抵抗」と捉えるべきです．このよう に捉えておかないと回路の設計はできません．`meter `kg s^-3 A^-2 では何 のことか解りません．

>無理解や曲解に基づいて，SIを「捻くれている」と評するのはどうかと思います．

私は MKSA 単位系は真空の誘電率／透磁率 `ε0, `μ0 を導入した単位系で あり，捻くれた単位系だと主張します．比例係数`ε0, `μ0 に単位次元まで 与えてしまったために無用の混乱を引き起こしています．磁石が絡んだ回路 設計では多くのエンジニアの多くが weber/ampere turn と gauss/oersted の混在で悩まされています．

真空の誘電率／透磁率は無次元の 1 とすべきです． `ε0, `μ0 の値や そ の単位次元に物理的な必然性はありません．SI 単位系を定めたとき既に存在 していた `ampere, `volt 単位を使い続けるるために，人間の都合で `ε 0, `μ0 を導入したにすぎません．

`ampere*`volt == `joule/sec を守りさえすれば良かったのですから，`ε 0 `μ0 なんて量を導入しなくても済ませられました．

MKSA 単位系では電荷同士に働く力は下のように表されます．

F = q q'/(4`π ε0 r^2)

ここで単位電荷 q を MKSA での値より

r=1`meter, q = !sqrt(1`newton `ε0 r^2) < 2.9756e-006 >

倍だけ小さくしてやれば `ε0 を 1 とできます．すなわち電流定義を現在の < 2.9756e-006 >倍にしてやれば電荷同士に働く力を

F = q q'/(4`π r^2)

と単純にできます．`ampere*`volt == wat == `joule/`sec の関係は，電圧 を < 336067 >== 1/< 2.9756e-006 > 倍にしてやることで守れます．

このような ε0，μ0 を無次元の 1 とした単位系が，飯田修一さんの「新電 磁気学」の教科書で MKSP 単位系として使われています．

MXK さんのレス (2007/04/15(Sun) 15:28)

これまでのことを整理してみると，SIがよくないということの根拠として，

1. 1クーロンに働く力が大きすぎる．
2. 基本単位であるキログラムにキロがついているのがよくない．
3. ε_0,μ_0 の導入がよくない．

を挙げられていました．これらはSIに対する文句のつけかたの典型ですが， これらは，単位系の構成の一般論や，電磁気学の体系に対する理解の 不足に起因するものです．

SIはかなりよく出来た単位系ですから，初学者は惑わされることなく， 安心して利用されたらよいと思います．なにより，分野，地域，時代を越えて 共通の単位系を共有できるということの利点には想像以上のものがあります．

(1) に関しては，もぐらたたきのようなもので，ある量を調整すると， 他の量が極端に大きくなったり，小さくなったりする，また考えている 状況によって，大小の基準は変わるということで，根拠にはなりえない ことが分かりました．

(2)に関しては，SIの基礎をなしている力学単位系のMKSの段階での選択だった わけで，電磁単位との関連で議論しても仕方がないのです．

(3)に関しては，話が複雑になるので，これまで議論を避けてきましたが， 締めくくりの意味で触れておきます．

小林＠那須さんが提案されているε_0, μ_0 を排除した 単位系は結果的にはローレンツ・ヘビサイド単位系になるのだと思います． 有理化(4πを除く)，MKS化したガウス単位系です．

しかし，ここでは電磁気的な基本単位は存在しません． 電流の単位は 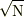, 電圧の単位は 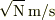です． これらをアンペア，ボルトと名づけることは可能かもしれませんが，いずれにせよ， 誘導単位にすぎません． ボルト，アンペアの基本単位として維持したいという元の主張とは逆の結果に なってしまっています．

> MKSA 単位系の名称から，単位を MKSA の四つだけで表そうとしますが，それ
> は誤りです．`volt も基本単位に加えて理解すべきです．

何度もいいますが，基本単位とするためには，その大きさに対する定義が必要です． 何度もたずねますか，「1ボルトの定義は何でしょうか？」 基本単位，すなわち次元を増やすと，誘導単位を基本単位で表す方法が一意に 決まらず困ることになります．

> でも抵抗の単位次元は `volt/`ampere と捉えるべきです．1 `ohmの抵抗は
>「 1 `volt の電圧を掛けたとき 1`ampere の電流が流れる抵抗」と捉えるべきです．

SIでもそのように理解しても全く問題ありません．既知の誘導単位同士から 新しい誘導単位を作ることは当然許されています． (MKSA では, グラムやセンチメートルが使えないので窮屈で困ると，勝手に 誤解している人がいましたけれど，ちょっと似てますね．)

基本単位と誘導（組み立て）単位の違いですが，

基本単位 他の基本単位の組み合わせで表せないよう独立なものを選ぶ その大きさを実現する装置，あるいは原理となる式や量が示されている

誘導単位 基本単位や誘導単位の組み合わせで表される 大きさは自動的にきまる

MKSA単位系は基本単位を4つとした4元単位系です．gaussやヘビサイド・ローレンツは 3元単位系です．

MKSA の基本単位とその大きさの定義は

メートルc=299792458 m/sと 1s キログラムキログラム原器 秒セシウム原子時計 アンペアμ_0=4π x 10^{-7} H/m と 1m, 1kg, 1s

のようになっています． gauss のような3元単位系ではアンペアの部分がないことになります． 力の単位から誘導される量なので，その大きさは自動的に決まるから です．

小林＠那須さんはこれにボルトを加えた，5元単位系を考えて おられるのですが，そうすると，別の定数(おそらく，cを用いて μ_0 と関連づけられない，独立したε_0)を導入することになって， 定数排除とは逆の方向ということになってしまいます．

> 比例係数`ε0, `μ0 に単位次元まで
> 与えてしまったために無用の混乱を引き起こしています．磁石が絡んだ回路
> 設計では多くのエンジニアの多くが weber/ampere turn と gauss/oersted
> の混在で悩まされています．

これは，複数の単位系が共存しているための混乱であって，SIだけの問題では ないでしょう．全く的外れの批判です．

> その理由として `ampere * `volt == watt と `newton `meter `sec^-2 を
> 同じ：== として扱いたいとする産業界からの要望があったとすれば納得でき
> ます．

産業界だけでなく，誰でも要望することです． 電気エネルギーと力学エネルギーをいちいち係数で換算するのは 困りますから．

> 1863 年に emu 単位系ができたときから practical units として
> `ampere, `volt が使われていました．また 1882 年にエジソンの電力システ
> ムが稼動を始めました．ですから 1880 年代に `ampere*`volt == watt を使
> った設計作業が多くなされるようになっはずです．その過程で cgs ではなく
> 比例係数を省略できる MKS が使われるようになったのだろうと推測します．

多分，そうなのだろうと思います．MKS のワットに整合させたのでしょう． そういう意味からも，SIはMKSの上にうまく収まったわけです． 時間を越えたconspiracyが働いたともいえます．

MXK さんのレス (2007/04/26(Thu) 22:29)

ScientificPython というのを使うと，単位つきの計算を電卓感覚で 行うことができます．(インストールが面倒なのがかなり問題ですが．)

• http://dirac.cnrs-orleans.fr/plone/software/scientificpython/

$ ipython -p physics Python 2.5.1c1 (release25-maint, Apr 12 2007, 21:00:25) IPython 0.7.3 -- An enhanced Interactive Python.

In [1]: L1 = 3.0 cm

In [2]: L2 = 1 inch

In [3]: L = L1 + L2

In [4]: L Out[4]: 5.54 cm

In [6]: L.inUnitsOf('ft') Out[6]: 0.1818 ft

In [8]: a = 300.0 m/s**2

In [9]: m = 2.0 kg

In [10]: f = m*a

In [11]: f Out[11]: 600 m*kg/s^2

In [12]: f.inUnitsOf('N') Out[12]: 600 N

In [4]: epsilon_0 = 8.854e-12 F/m

In [5]: Q = 1.0 C

In [6]: r = 1.0 m

In [7]: F = Q**2 / (4*pi*epsilon_0*r**2)

In [8]: F Out[8]: 8.988E+09 C^2/m/F

In [9]: F.inUnitsOf('N') Out[9]: 8.988E+09 N

In [10]: F.inUnitsOf('GN') Out[10]: 8.988 GN

小林＠那須 さんのレス (2007/04/27(Fri) 09:11)

MXK さん，こんにちは．私も python 使いです．私も python が物理・工学 の分野で，もっと使われて欲しいと思っています．

Enthought の package を install しているので，既に Scientific.Physics も入っていました．でも，このモジュールは知りませ んでした．試してみたのですが，御示しのようには動きません．下のように 働かせられる所までで精一杯でした．

//@@ import Scientific.Physics.PhysicalQuantities as pq

l = pq.PhysicalQuantity(10., 'm') big_l = pq.PhysicalQuantity(10., 'km') print big_l + l t = pq.PhysicalQuantity(314159., 's') print t.inUnitsOf('d','h','min','s')

p = pq.PhysicalQuantity # just a shorthand...

e = p('2.7 Hartree*Nav') e.convertToUnit('kcal/mol') print e print e.inBaseUnits()

freeze = p('0 degC') print freeze.inUnitsOf ('degF') //@@@

10.01 km (PhysicalQuantity(3.0,'d'), PhysicalQuantity(15.0,'h'), PhysicalQuantity(15.0,'min'), PhysicalQuantity(58.999999999980446,'s')) 1694.2757596 kcal/mol 7088849.77818 kg*m**2/s**2/mol 32.0 degF

私は IPython を使っていません．(昔 IPython でトラブルがあって使う気に なれません．既に python ディレクトリに入ってはいるのですが．)-p physics の意味が解っていません．できたら上のような import が明確な，単独で動く python コードを例示していただけないでしょうか．

P.S. No.15326 への返答するのが礼儀なのは解っています．でも非難がまし くなりそうで避けています．部分的にではなく全体を整理・纏めた形で，自 分の考えを述べさせてもらいたいと思っています．でも MKSA 単位系につい ては込み入った論理展開となります．面倒な作業となります．連休あけまで 時間を下さい．

MXK さんのレス (2007/04/28(Sat) 09:49)

小林＠那須さん，

残念ながらPython全くの素人です．今回もubuntuの最新版で関係のパッケージを 放り込んだだけです．

L1 = 2.0 m

などとかけるのは，ipython (Interactive Python) がプリプロセスしているため です．ipython を使わないのであれば，プリプロセッサを作る必要があります． すぐできそうですが．

ipython は単純な代入の場合しかダメみたいですが，

2.0 m + 1.2 ft

とか書けるようにすると便利だと思います．

本題の方，全然急ぎません

小林＠那須 さんのレス (2007/04/29(Sun) 08:38)

MXK さん，お返事ありがとうございます．

>残念ながらPython全くの素人です． Python は物理での数値計算に適した sci.py などのモジュールがあります． 下の拙稿は，できるだけ手っ取り早く python で行列・ベクトル計算できる ように書きました．読んでみてやってください．

python での行列・ベクトル数値計算;; http://www.nasuinfo.or.jp/FreeSpace/kenji/sf/fastTour/pyLinear.htm

現代のコンピュータを使えば Ramanujan 級の計算能力を自分の物にできます． 行列やベクトル計算でも scalar 計算と同じ手間で計算できてしまいます． これを活用すべきと主張します．現代物理では式を導くだけで実際の数値計 算を省略してしまうことが多いのですが，これは間違いだと主張します．具 体例で計算してみるだけで，式だけでは見逃していた多くのものが見えてき ます．

>L1 = 2.0 m などとかけるのは，ipython (Interactive Python) がプリプロセスしているため

unit.py モジュールを作って meter=1; mile = 1609.3 などと MKSA 単位系 での値を設定しておいてやり，from unit import * を行えば python で単位 系つきの演算ができるようになります．でも名前空間を汚すので，あまり奨 められません．ipython でプリプロセスすることは単位文字列が予約語にな るわけで，名前空間を汚すのと似たようなものだと思います．

>2.0 m + 1.2 ft とか書けるようにすると便利だと思います．

拙作 の sf.exe ならば，sf.ini ファイルに単位の MKSA 値を設定してある ので下の計算が可能です． 2`meter + 1.2`feet < 2.36576 >

主だった物理定数も指定してあるので，真空の誘電率を含んだ下の計算も可 能です．sf.ini はユーザーも編集できるテキスト・ファイルであり，任意の 単位／物理定数を設定できます． sf "q=1`coulomb, r=1`meter, q^2/(4`π `ε0 r^2)" < 8.98755e+009 >

特に行列／ベクトル演算も可能なのが sf の自慢です．Windows 用ですが， 単なるコンソール・ソフトなので VMWare などが動いていれば sf.exe も動 くと思います．下にマニュアルがあるので，こちらも見てやってください．

• http://www.nasuinfo.or.jp/FreeSpace/kenji/sf/fastTour/sfFastTour.htm

MXK さんのレス (2007/05/01(Tue) 16:58)

PhysicalQuantityは「物理量」というオブジェクトを定義して，次元をちゃんと管理して いるところが買いだと思います．

一方，

> 拙作 の sf.exe ならば，sf.ini ファイルに単位の MKSA 値を設定してある
> ので下の計算が可能です．
>2`meter + 1.2`feet
>< 2.36576 >

のような（実質上）無次元の計算は他の方法でもできるので，あまり興味がありません．

sfのように単位や物理定数を単に数因子として扱うと，その中途半端さゆえに， いろいろ支障が出てくると思います．そもそも，このスレッドのタイトルも， その辺りに原因があるのではと想像しています．

sfのユーザではないので，断定はできませんが，No.15495 の例は一部しか再現できない のではないでしょうか？

小林＠那須 さんのレス (2007/05/02(Wed) 14:02)

>PhysicalQuantityは「物理量」というオブジェクトを定義して，次元をちゃんと管理して >いるところが買いだと思います．

MXK さんは「次元の管理」で hysicalQuantity クラスに何をさせようとして いるのでしょうか．

私が数式に `meter, `kg などの単位次元を書き込む目的は，数式の物理的意 味を明示したいからです．例えば下のように書くことで，エネルギーを求め る計算をしていることを明示したいからです．数値だけの計算の意味では下 の `meter, `sec, `kg は全て 1 であり無意味です．

v = 2`meter/`sec, m=0.5`kg, E = 1/2 m v^2 < 1 >

下のような式では，コメントで補ってやらないと，数式の物的意味が分り難 くなるからです．

v = 2, m=0.5, E = 1/2 m v^2 # v is velosity in MKS unit < 1 >

計算結果の単位次元を明示することは，答えを欲しがっている人が分ってい るはずでありあまり意味がないと思っています．また結果の単位次元は一意 に決まりません．たとえば抵抗の単位次元を `ohm で表したい人と`meter `kg^-1 `sec^4 `ampere^2 で表したい人がいます．この意味で，私は計算結 果の単位次元を自動表示することは面倒なわりに益が少ないと思っています．

これで「No.15495 の例は一部しか再現できないのではないでしょうか？」の 答えにもなっているつもりです．どうでしょうか．

MXK さんのレス (2007/05/02(Wed) 22:40)

> 私が数式に `meter, `kg などの単位次元を書き込む目的は，数式の物理的意 > 味を明示したいからです．例えば下のように書くことで，エネルギーを求め > る計算をしていることを明示したいからです．数値だけの計算の意味では下 > の `meter, `sec, `kg は全て 1 であり無意味です．

声も出ないほど，驚いています． 物理量に関する認識が誤った状態で，MKSAやSIを云々されていることに 今さらながら驚いています．以前にお示ししたSI文書

• http://www.bipm.org/utils/common/pdf/si_brochure_8_en.pdf
• http://www.nmij.jp/chishiki/SI8J.pdf

の冒頭の第一文

1. 序章 1.1 量と単位 量（quanity）の値（value）は一般に数字（number）と単位（unit）の積と して表される．単位とは単にその量の基準となる特別な例のことであり，数 字は「単位」に対する「量の値」の比を表す

でさえ理解しておられないことが明白になりました．

物理量の意味が分からなければ，それをオブジェクトとして実装するメリットが 分からないのは当然です，そして，PhysicalQuantityパッケージのよさが 分からないのも当然です．

単位や次元，物理量に対する，このような軽薄な認識に基づいて，現在の科学技術の 重要な基盤であるSIを声高に批判されることは，くれぐれも控えていただきたいというのが， 私の切なる希望です．

くどいようですが，sfにはできない（であろう）例をもう一つあげておきます．

In [1]: L = 2.3 m

In [2]: S = 3.5 m**2

In [3]: S + L <type 'exceptions.TypeError'>: Incompatible units

In [4]: S + L**2

Out[4]: 8.79 m^2

エラーが出ているだけだと思われるかもしれませんが，次元の異なる量は加算できない， と判断できているところが素晴らしいところです．

連休明けの課題ですが，前提となる認識が今のままでは，双方時間の無駄になる だけですので，出していただく必要はないと思っています．

小林＠那須 さんのレス (2007/05/03(Thu) 08:41)

私は非難がましいことを書くことを避けてきました．でも今回は MXK さんに合わせてみます．

>エラーが出ているだけだと思われるかもしれませんが，次元の異なる量は加算できない， >と判断できているところが素晴らしいところです． ・ >そして，PhysicalQuantityパッケージのよさが分からないのも当然です．

sf で単位を書かせるのも目的は同じです．提示された式を sf ではエラーに することなく計算するのは御指摘どうりです．でも それが問題とは思ってい ません．物理量を理解している方ならば，下のような式を書いた時点で誤り に気付くはずだからです．

3.3`mm + 3.5 `mm^2

また PhysicalQuantityパッケージを素晴らしいといっていますが，その MXK さんが python を使い込んでいないのは明白です．一年後には，その素 晴らしい PhysicalQuantity を使っていないでしょう．Python の理工学への 応用の力点はそんな所にはありません．理工学系の python 利用者でも，大 部分は PhysicalQuantity など使っていません．scipy tutorial ぐらい読ん でおいてください．自分が少し使ってみただけのソフトを無責任に他人に奨 めるのは如何なものかと思います．

ついでに．用語としては PhysicalQuantities モジュールであり PhysicalQuantity クラスです．PhysicalQuantityパッケージなぞありません．

>量（quanity）の値（value）は一般に数字（number）と単位（unit）の積と >して表される．単位とは単にその量の基準となる特別な例のことであり，数 >字は「単位」に対する「量の値」の比を表す >でさえ理解しておられないことが明白になりました．

sf で単位をつけるのはドキュメント性のためだと言っているのに なぜ無視 するのですか．MXK さんの読解力を疑うべきかとも思い始めています．

SI 単位系の規格は結果をまとめてあるだけです．理由は書いてありません． 2e-7 の数値が出てきても，その数値の理由まで書いてありません．F. Gauss, J.C. Maxwell の巨匠たちが作り上げた emu 単位系を，SI 単位系で は捨てた理由を書きません．SI 単位系よりも，既に存在していた emu 単位 系のほうが合理的・単純・素直・奇麗なのに．

Guass/Maxwell が eum 単位系を absolute unit system と傲慢とさえ形容で きる言い方した理由が MXK さんは分っていません．分ろうともしない方なの でしょう．

MXK さんは権威のある文書に書いてあることを暗記するだけで納得できる方 に思えます． SI の規格書に書いてあるからといって抵抗の単位次元を `meter `kg^-1 `sec^4 `ampere^2 で良いとすることが，権威への盲従根性を あらわしています．実務で「100 `meter `kg^-1 `sec^4 `ampere^2 の抵抗」 と言っても通用しません．100 `ohm の抵抗と言わねばなりません．`meter `kg^-1 `sec^4 `ampere^2 が物理的に何を意味するのか考えようともしない のでしょう．MXK さんにとっては単位は符丁であり，その誤りはソフトウェ アで検出できれば良いのでしょう．

>だけですので，出していただく必要はないと思っています． 曲解と権威への盲従で頓珍漢な批判をするだけならば読まないでください． 黙っていてください．

2ch ではないのですから上のようなやりとりは避けるべきと思います．MXK さんも同意願えますでしょうか．もちろん，誤りへの厳しい指摘はあって当 然です．でも その前に意味の確認ぐらいは成されるべきです．読み誤って いることもあるのですから．如何でしょうか．

toorisugari no Hiro さんのレス (2007/05/03(Thu) 18:13)

単なる横やりです．無視してください．

小林＠那須さんは，objectという概念，物理的(幾何学的)な意味でもコンピュータの意味でも，を理解されていないように思えます．

# 上手に説明せよと言われてもできませんが．．．

MXK さんのレス (2007/05/03(Thu) 19:23)

小林＠那須さん，

> 私は非難がましいことを書くことを避けてきました．でも今回は MXK さんに合わせてみます．

私もそうしてきたつもりですが，これまでの議論の中で，緩い球は無視されたり，曲解される傾向が あると感じたので，失礼を承知で強く書いてみました．

> sf で単位をつけるのはドキュメント性のためだと言っているのに なぜ無視
> するのですか．MXK さんの読解力を疑うべきかとも思い始めています．

何も sf にケチをつけるのが本意でないのです． コメントとして単位を書くより，少しマシであることは認めます．また単位計算以外の機能に 関しては知らないので何もいうべきことはありません．ただ，

(1) sf における単位，次元の扱いは不完全である．(単位を数因子として考えているため， 計算結果が数になって次元の情報が失われてしまっている．引き続き計算する場合には 再度単位を付加する必要がある．) (2) 正しい単位，次元の考え方に基づいて実装した例としてPhysicalQuantityがある．

といっているだけです．

これまでの議論の流れから，小林＠那須さんが単位や単位系に関して，通常とはかなり 異なった理解をされており，それが今回の SI, MKSA 批判（ひねくれた単位系)の原因だと いうことが分かってきました．

今回，直接関係のない，sf について触れたのは，単位計算ができることを，ご自分で 宣伝されていたので，拝見させていただいたからです．しかしながら，内容を見て かなりガッカリでした．昔から，単位計算のできる電卓プログラムを作りたいと考えていたので， これを機会につくり始めよう思い，先行例を探しているうちに，PhysicalQuantityにゆきあたりました． 要求仕様を十分満足しているので，作る必要はなくなりました．

そして，(1), (2) は本質的に異なったレベルにあるという点をお知らせしましたが， sfで十分との返答をいただいたので，単位や単位系に関するご理解が通常とは 異なっていることを再度認識させられた次第です．

> SI 単位系の規格は結果をまとめてあるだけです．理由は書いてありません．
> 2e-7 の数値が出てきても，その数値の理由まで書いてありません．

以前にもいったかも知れませんが，この数値はそれまで使われていたアンペアの 大きさをできるだけ変えないためです．この数値をいじるとアンペアの大きさが 変化するだけで，定性的な部分は何も変わりません． この数値に拘って，全体像を見失っていらっしゃると感じています．

今問題にしているのは，それ以前の問題です．SI文書を提示したのは，全部を読んで 下さいということではなく，その冒頭にある，単位や単位系の考え方を理解して いただきたかったからです．（単位系に関する参考書なら何でもいいのですが， 正確さとアクセスの容易さから挙げたにすぎません．オペアンプのデータシートの ようなもので，権威とは関係ありません．）

1. 物理量は

（物理量）= (数値) × (単位)

と表すことができる．単位自身も物理量である．

(ii)単位系においては，少数の基本単位を選定する．他の単位は基本単位の組み合わせに帰着できる

ように定義する．

3. 基本単位の大きさを実際的に定める方法を定義する．（標準）

ぐらいのことはきちんと押さえていただかないと，議論ができないと思います． 下の，オームに関する議論は (ii) を理解されていないことの反映ではないでしょうか． sfのように，単位を数と思うのは (i) に合致していません． (iii)についても， 何度かお尋ねしたと思いますが，返事をいただいた記憶がありません．

SI以外の単位系に対しても，上の考え方は当然適用されます．

> F. Gauss, J.C. Maxwell の巨匠たちが作り上げた emu 単位系を，SI 単位系で
> は捨てた理由を書きません．

Gauss, Maxwell は権威ではないのでしょうか？

> Guass/Maxwell が eum 単位系を absolute unit system と傲慢とさえ形容で
> きる言い方した理由が MXK さんは分っていません．分ろうともしない方なの
> でしょう．

"absolute" というのは，次元や単位を物理法則に基づいて決めることを意味して おり，SI単位系もれっきとした absolute unit system です．

(absoluteは「絶対的によい」とか「究極」という意味では決してありません．)

> SI の規格書に書いてあるからといって抵抗の単位次元を
> `meter `kg^-1 `sec^4 `ampere^2 で良いとすることが，権威への盲従根性を
> あらわしています．実務で「100 `meter `kg^-1 `sec^4 `ampere^2 の抵抗」
> と言っても通用しません．100 `ohm の抵抗と言わねばなりません．`meter
> `kg^-1 `sec^4 `ampere^2 が物理的に何を意味するのか考えようともしない
> のでしょう．

別に規格書によらずとも，P = I^2 R という式(物理法則)を知っていれば，オームを 基本単位で表すと，

Ω = W / A^2 = J / s A^2 = kg (m/s)^2 / s A^2 = kg m^2 s^{-3} A^{-2}

となることはだれでも簡単に求められます．また，

In [13]: R = 1 ohm In [14]: R.inBaseUnits() Out[14]: 1 kg*m^2/A^2/s^3

と自分に間違いがないか検算もできて，安心できます．

物理的意味は P = I^2R で十分でしょう．

量子ホール効果では h/e^2 (h; プランク定数， e: 素電荷) という量が出てきますが， これも抵抗の次元を持っています．Ω = J s / C^2 でもあるわけです．

（emu だと，抵抗の単位は cm/s になると思いますが，こちらだと物理的意味は もっと明白なのでしょうか？）

このスレッドの目的である，なぜ 1kg なのか，あるいは派生して 1A，μ_0, ε_0 について 本気で理解したいと考えておられるのなら，先入観を排除して，単位系の基礎に ついて丁寧に勉強しなおすことを強くお勧めします．結局それが早道だと思います． 中途半端な理解に基づいて，「ひねくれた単位系論」を展開されても全く生産的では ありませんし，初学者を混乱させるだけです．

このことをお伝えしたく，強めの球を投げています．非礼を再度おわびします．

toorisugari no Hiro さんのレス (2007/05/03(Thu) 20:06)

MXKさん

> (i) 物理量は
> （物理量）= (数値) × (単位)
> と表すことができる．単位自身も物理量である．

ありがとうございます． 漠然とした「単位自身も物理量」であるという感覚を今まではっきり文章化できていなかったので，すごく，すっきりとしました．

小林＠那須 さんのレス (2007/05/04(Fri) 08:18)

あまりに初等的なので捨てようかと思っていた説明文ですが，ここに書いて みます．MXK さんの誤解を晴らす役目はしてくれそうです．

●物理量は単位を伴った数値です．単位と数値の組によって物理量が等しい か否かが決められます．大小関係が決められます．

○長さ:1`meter と 面積：1`meter^2 は比較できません． 1`meter の長さと 1`meter^2 の面積は，数字は同じ 1 であって数字が等し くても，物理量としては等しくありません．`meter 目盛りの物差しを使えば 1 である面積は，`inch 目盛りの物差しを使えば，異なった値となってしまい ます．

長さ 1`meter を inch で表せば 33.37 `inch です． sf "`meter/`inch" < 39.3701 >

面積 1`meter^2 を inch の単位で表せば 1550 `inch^2 です．下の換算係数 が必要です． sf "(`meter/`inch)^2" < 1550 >

このような換算係数の導入は，単位系の作成において避けるべきです．換算 係数を必要としない，単位系全体に渡って整合性持った単位系を作成すべき です．

MKSA 単位系は，この整合性を意識的に放棄しています．電磁気の世界は，エ ネルギー・力のやりとりによって M K S:質量・時間・長さの世界と結びつい ています．この力・エネルギーと結びつけるときに係数が 1 となる結び付け 方となるように単位系を定めるべきです．でも SI 単位系は，そうしません でした．しかも，二箇所で換算係数を導入しています．それが μ0 と ε0 です．電流定義の個所と，電圧の導入の個所です．この意味で MKSA `volt 単位系と言った方が良いと主張します．

○ 物理方程式は単位系によって形を変えるものであってはなりません． `meter 単位の物差しは人間が地球の子午線の長さから定めたものです．この 単位を使い面積を求める公式を記述できます．辺の長さ L `meter 正方形の 面積を S `meter^2 とすると下の式がなりたちます．

S = L^2

辺の長さ 10 `meter 正方形の畑の面積は S は 100 `meter^2 です．辺の長 さが゛10`meter の正方形の畑の面積は，1`meter^2 の小さな畑 100 個の面 積と同じです．

○ 単位系が統一されていないと，変換係数が入り込んできます． 長さを `meter で，面積を `inch^2 で表現していると S = 1550 L^2 # 1550 unit dimention is (`inch/`meter)^2

余分な係数の入らない S = L^2 の公式を成り立たせるためには，単位系を統 一しておく必要があります．MKSA 単位系は，意識的に `ε0 `μ0 の換算係 数を導入しています．ここを捻くれていると私は主張します．

●基本単位から誘導される単位系の体系 単位系は，基本単位からの誘導単位を導く連鎖の体系として理解していなけ ればなりません．物理量を扱うときは，その単位次元も常にペアとして意識 していなければなりません．

○ 圧力単位 pascal 圧力 10`k pascal といったとき

10 `k `newton/`meter^2 == 10 `k `kg `meter^-1 `sec^-1

の式の連鎖を，物理定数表などを見ることなく導き出せなければ圧力という 物理量を理解できているとは言えません．この程度の単位の誘導は物理・工 学に携わっているものは簡単行います．

MKSA 単位系では，電流定義だけから誘導単位を誘導していく上の連鎖が行え ません．電圧を導入した個所 V I = `joule/`sec を潜り込ませまる必要があ ります．SI 単位系の規格は，その潜り込ませに言及することなく，M K S A の単位次元の表を並べるだけで済ませます．

PM14:57 追記 すいません，ここから下は無しにしてください．磁荷の φ と∂φ/∂t の φ は同じにできました．恥ずかしい誤りです．

>Ω = W / A^2 = J / s A^2 = kg (m/s)^2 / s A^2 = kg m^2 s^{-3} A^{-2}

>となることはだれでも簡単に求められます．...

同様なことを磁界の側の基本単位 `weber について行えますでしょうか． これが出来ないことが，捻くれた MKSA だとする理由の一つです．

ただし「∂φ／∂t = 電圧」からの説明は反則です．それだったら φ を基 本単位にすべきだからです．

私は今まで何度も磁荷の単位 `weber を簡単に誘導できないことに言及して います．これが磁石の分野で weber が浸透しない理由でもあります．そして MXK さんに答えてもらっていません．今回は答えていただけますでしょうか．

小林＠那須 さんのレス (2007/05/04(Fri) 09:18)

>緩い球は無視されたり の理由を書きます．

>から，単位計算のできる電卓プログラムを作りたいと考えていたので， >これを機会につくり始めよう思い，先行例を探しているうちに，PhysicalQuantityにゆきあたりました．

どちらが先行しているかは知りませんが，単位も扱える電卓として google 電卓が有名です．記述方法としても下のように合理的にできています．

16 MB / 10 minutes in Kbps -> 218.453333 Kbps 1 MB + 256 bytes in bytes -> 1048832 bytes

Google 電卓も発表されたとき単位系も扱えると評判になりました．でも現在 MKX の周囲で google 電卓の この機能を使っている方がどれほどいるでしょ うか．Google を何時でも使える環境にいる理工学系の学生でも，一週間に一 回も google 電卓を使っていないのが現実でしょう．

私は PhysicalQuantity が無意味だと言っていません．面倒だから多くの人 に使ってもらえないと言っているだけです．

No.15634, No.15652 の話の流れをすっきりさせるには枝葉を捨てて，幹の部 分に集中すべきです．このような単位系のソフトに言及すると，話を混乱さ せやすくなります．今回は敢えて こちらにも言及しますが，今までだったら 言及していません．

枝葉と幹の判断が MXK さんとは異なることがあると思います．また非難がま しくなりそうで返答を避けることもありました．でも誤魔化そうとしたこと は一度もありません．ここらは MXK さんも同じはずです．

無視しているのではなく避けていることを御理解ください．

MXK さんのレス (2007/05/04(Fri) 17:59)

気になる部分のみコメントします．

> ●物理量は単位を伴った数値です．単位と数値の組によって物理量が等しい
> か否かが決められます．大小関係が決められます．

物理量は数値ではないので，第一文は紛らわしいです．物理量は単位(ものさし)を決めて 計量することによって，はじめて数値化されます． 単位も物理量であり，自分自身で計ることで，1 という数が得られます． 極端にいえば，単位がなければ，物理量は数と関係づけられません．

> 面積 1`meter^2 を inch の単位で表せば 1550 `inch^2 です．下の換算係数
> が必要です．
> sf "(`meter/`inch)^2"
> < 1550 >
> このような換算係数の導入は，単位系の作成において避けるべきです．換算
> 係数を必要としない，単位系全体に渡って整合性持った単位系を作成すべき
> です．

ここで係数が現れる理由は，同一の次元(長さ)に対して，複数の単位を導入した からです．これは「単位系」において係数の出現を避けるという話とは直接関係がありません．

問題なのは，長さの単位をマイル，面積の単位をエーカというように, 独立に決めてしまうと， In [5]: S = 1 acres

In [6]: L = 1 mi

In [7]: S / L**2 Out[7]: 0.0015625000000000001

のように，無次元の係数が現れることです． これを避けたものが，「一貫した単位系」，あるいは「コヒーレントな単位系」 と呼ばれます．この例では，面積の単位として平方マイルを使うか，それに 適当な名前をつけることで，係数を1にできます．

> MKSA 単位系は，この整合性を意識的に放棄しています．電磁気の世界は，エ
> ネルギー・力のやりとりによって M K S:質量・時間・長さの世界と結びつい
> ています．この力・エネルギーと結びつけるときに係数が 1 となる結び付け
> 方となるように単位系を定めるべきです．でも SI 単位系は，そうしません

完全に間違っています．MKSA単位系は「コヒーレントな単位系」です． 基本単位と誘導単位の換算係数はすべて1になっています．

> でした．しかも，二箇所で換算係数を導入しています．それが μ0 と ε0
> です．電流定義の個所と，電圧の導入の個所です．この意味で MKSA `volt
> 単位系と言った方が良いと主張します．

「μ0 と ε0は換算係数ではなく，物理量です．」

＊真空中の光速 c や重力定数 Gと同じように次元をもった量です． ＊(同一次元の)単位間の換算には使われていません．そのような 換算係数は無次元量でなければなりません． ＊これらは単位でもありません．

μ0 と ε0を勝手に換算係数と決め付けて，MKSA をインコヒーレントな単位系だと 信じこんでおられるのですね．はなはだしい曲解です．こんなひねくれた見方を すれば，どんなに真っ直ぐなものでもひねくれてしまうでしょう．

おすすめのemuでは，μ0 は無次元量ですが，ε0 は 1/c^2 です． これは換算係数とはいえないでしょう．そうだとすると c も換算係数になって しまいます．

c が長さと時間の換算を行っていると理解することもできますが， このように次元の異なる量をつなぐ物理量の数値は1にはならないのが， 一般的です．cgs でも MKS でも，c の数値は1ではありません． このことに文句をつける人はいないでしょう．μ0 と ε0が 1でない数値で表されることだけを問題にするのは，全く論理的では ありません．

> MKSA 単位系では，電流定義だけから誘導単位を誘導していく上の連鎖が行え
> ません．電圧を導入した個所 V I = `joule/`sec を潜り込ませまる必要があ
> ります．SI 単位系の規格は，その潜り込ませに言及することなく，M K S A
> の単位次元の表を並べるだけで済ませます．

V = P / I という関係式をなぜ避けておられるのでしょうか？ 高校生でも知っている式を「潜り込ませる」とは一体どういう意味なのでしょうか？

1アンペアの電流を可変抵抗に流して，1秒あたりの熱量が1ジュールになるように 抵抗を調整したときの，抵抗の両端の電圧を1ボルトと定義すればよいだけです． （モータや電熱器は電気で働いていることを忘れておらえるのでしょうか？）

小林＠那須さんに，このような物理的実現（ハードウェア）に関する リアリティが伝わらないのがとても不思議なことです．回路をやっておられるのに 1ボルトをどのように実現するかに，関心を示されないのは不思議なことです． 単位や物理量を式や紙の上のことのように考えておられる印象をもってしまいます．

以下は書いてしまっていたので残します． /* ----------------------------------------------------------------------- >>Ω = W / A^2 = J / s A^2 = kg (m/s)^2 / s A^2 = kg m^2 s^{-3} A^{-2} >>となることはだれでも簡単に求められます．...

> 同様なことを磁界の側の基本単位 `weber について行えますでしょうか．
> これが出来ないことが，捻くれた MKSA だとする理由の一つです． ::

> ただし「∂φ／∂t = 電圧」からの説明は反則です．それだったら φ を基 > 本単位にすべきだからです．

どうして，反則なのでしょうか．これはちゃんとした物理法則です．S = L^2 と同じです．

1ボルトの大きさは上のように(誘導単位として)決定されているので，基本単位の１つである 1秒と組合わせて，新しい誘導単位 ウェーバを

1 Wb = 1 V × 1 s

と定義することができます．

「それだったら φ を基本単位にすべきだからです．」といわれる根拠が全く分かりません． きっと，とんでもない勘違いをされているのだと思います．

> 私は今まで何度も磁荷の単位 `weber を簡単に誘導できないことに言及して
> います．これが磁石の分野で weber が浸透しない理由でもあります．そして
> MXK さんに答えてもらっていません．今回は答えていただけますでしょうか．

磁性の分野では，SIへの移行が遅れている分野の１つです．現在は徐々に改善されているようです． たとえば，超伝導磁石の強さは例外なくテスラで書かれています． ----------------------------------------------------------------------------------- */

小林＠那須さんが，とんでもない間違いをされている理由を考えていますが，なかなか分からずに います．

いくつかの原因が考えられますが，

0. 換算係数と物理量の区別ができていない．
1. 物理量を数値に重点をおいて捉えている．
2. 単位が物理量であることが納得できていない．
3. 誘導単位と基本単位の関係が理解できていない．
4. 具体的に単位の大きさを決める操作(標準の定義)の必要性に気づいていない．

最後の点に関しては，組み立て単位が一旦定義されてしまえば，基本単位と対等の資格をもって， 他の組み立て単位の定義に使える，ということを理解されていないような印象をもっています． Wb, V, Ωあたりの議論から，そう感じています．

基本単位の役割の1つは, 2つの誘導単位が互いの定義に現れて，循環定義になってしまうことを 避けるためです．

たとえば, A := W / V, V := W / A において，アンペアかボルトのどちらかが先に決まっていないと， 困ったことになるからです．

基本単位はその大きさを実際に作るための手段が提供されている必要があります．これは組み立て単位と の大きい違いです．（ユーザにとっては関係ないのかも知れませんが．）

「ボルトも基本単位に加えるべき」と主張されていますが，そのためには，ボルト原器（標準）を 作る必要があります．そうすると，今度はこうしてつくったボルトとこれまでのアンペアの積が，力学的に 決まるワットを一致する保証がなくなってしまいます．基本単位の数はむやみに増やせないのです．

このあたりは，これまでの議論でも，繰り返し説明してきたのですが，知ってか知らずか殆ど無視されてきました．

＃ 解説として，正しく書いておられる部分も多いのですが，根本のところで間違っているので，何とも しようがありません． 1 = 2 を前提に数学理論体系を作っているような感じです．しかも既存の体系 が変だと主張されているわけですから，困ってしまいます．

＃「絶対単位(系)」，「一貫した単位系」など，単位を考える上での基本概念を完全に誤解しておられるのですから， くれぐれも，基本に立ち戻って勉強されることをお勧めします．

小林＠那須 さんのレス (2007/05/06(Sun) 07:56)

MXK 様，自分の電磁単位系の誘導順序の誤りに気付きました．MXK 様が長々 と議論に付き合ってくれたおかげです．有難うございました．

MXK 様には途中で感情的な文章を投げたりして失礼しました．MXK 様が根気 よく議論に付き合ってくれたことに感謝しております．自分の基本的な誤り に気付かないまま恥をさらし続けるところでした．

今回の議論を踏まえ「捻くれた SI:MKSA 単位系」ではなく「分り難い SI:MKSA 単位系」として自分の頭の仲を文章化してみます．まとまった段階 で また皆様の御批判を伺わせて頂ければと思います．

m( __ __ )m.m( __ __ )m.m( __ __ )m.m( __ __ )m.m( __ __ )m.m( __ __ )m.

MXK 様には借りができてしまったと思っています．何か御返しをすべきとも 思っています．

Python ならば御返しができるかとも思います．私は sf， Python, Maxima と組み合わせで理系のコンピューター計算を何年も行わせています．(以前は Mathematica3.1 を使っていましたが，現在はインストールしていません． 三つのソフトの組み合わせのほうが便利だからです．)こっち方面なら少しは 自負しても良いと勝手に思っています．

Python で一番驚いたのは vpython でした．物理の教育向けに作ったそうで す．十数行で落下運動の 3D アニメーションが記述できてしまうのを見せら た時は驚愕するばかりでした．

下にデモ・ビデオがあります．英語での説明ですが聴き取りやすい英語です． MXK さんなら理解できるかと思います．下の URL の最初にあるビデオで落下 運動の 3D シミュレーションのアニメーションをデモしています．

• http://vpython.erikthompson.com/

別に押し付ける気はありませんが，少しだけでも御礼のつもりで紹介させて もらいます．

MXK さんのレス (2007/05/06(Sun) 11:37)

小林＠那須さん，

解決したようで，私もホッとしています． 「分かり難い」というタイトルはどうかと思いますが，新しい理解を まとめていただくのは，よいことだと思います．

昔の単位系がよくて，今の単位系が悪いと主張されるのは，大抵の場合，年配の 方で，学生時代に習ったものを固持する立場からです．（若い人がそれを聞いて 鵜呑みにしているケースも多いです．）

回路でいえば，真空管は分かるが，トランジスタは分からん，というのと類似の 現象です．

人間はどうも「学び直す」というのが苦手のようです．

python のおすすめありがとうございます．PhyisicalQuantityのコードを少し触りはじめています． 指示した単位で括るという機能を追加してみました．

In [1]: ph = 1.2 V*s

In [2]: ph.inUnitOf('Wb') Wb Out[2]: 1.2 Wb

In [3]: ph.inUnitOf('T') T*m**2 Out[3]: 1.2 m^2*T

In [4]: ph.inUnitOf('N') N*m/A Out[4]: 1.2 m*N/A

In [5]: ph.inUnitOf('A*ohm') A*ohm*s Out[5]: 1.2 A*ohm*s