ＳＡＴＹ さんの書込 (2007/03/20(Tue) 11:18)

「物理のかぎしっぽ」様いつも活用させていただいております． 「物理のかぎしっぽ」ホームページの中の「物理数学」→「変数分離形」で dy/dx=f(x)g(y)を展開するために，両辺に dx を掛けて dy=f(x)g(y)dx としておりますが， dy/dx=f(x)g(y) ↓（両辺に dx を掛けて） dy=f(x)g(y)dx のような展開はなぜ．できるのですか？ どうしても両辺に dx を掛けるということが理解できないのです．dy/dx はyをxで微分することを表しており，割り算を表しているのではないと理解しております．ちなみに，私の数学の理解度は高校数学レベルです． 私の理解不足で大変申し訳ございませんが，アドバイスの程宜しくお願い致します．

toorisugari no Hiro さんのレス (2007/03/20(Tue) 14:14)

> dy/dx=f(x)g(y) > ↓（両辺に dx を掛けて） > dy=f(x)g(y)dx > のような展開はなぜ．できるのですか？ > どうしても両辺に dx を掛けるということが理解できないのです．dy/dx はyをxで微分することを表しており，割り算を表しているのではないと理解しております．

微分(商)は微少変位(=全微分)の分数と考えて差し支えありません．

滑らかな関数なら，そのグラフを十分に拡大していくと，どんなに曲がった曲線でも，直線に見えてきます． # ちょうど地球上にいる我々は地面が平板だと思いこんでるように．

そこにおいて，適当な2点間のxの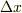変位 とyの変位 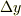の比 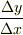は直線の傾きになり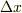， を(視野に入る範囲で)どのような大きさに採ろうとも，比の値は(ほとんど)変わりません．

ですから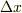， の大きさ(あるいは区間)を明示する必要がなくなり，どの点から測ったのかだけが意味を持ちます(この場合ルーペの中心がある地点のことです)．このとき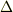， を 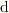に書き換えたものを「その点における傾き」と考えます．これが微分(商) 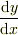です．

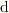# という記号は「曲線が直線に見えるくらい拡大したグラフにおける変位」を採る操作，つまり「微小変位」を採る操作(=微分)であることを表します．

ですから分数と考えてかまいません．

ＳＡＴＹ さんのレス (2007/03/20(Tue) 15:25)

toorisugari no Hiro様ありがとうございます．toorisugari no Hiro様の説明は納得することができますが， dy/dx=f(x)g(y)から両辺にdxを掛けて dy=f(x)g(y)dx を求めるのではなく，微分法等の公式を活用して，dy=f(x)g(y)dx を求めることはできないのでしょうか？ お手数おかけ致しますが，宜しくお願い致します．

toorisugari no Hiro さんのレス (2007/03/20(Tue) 16:13)

裸の 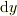, 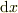を使うのなら，そもそも先の考えが基本であり，それを導く公式も何もないのですが．．．

分数と思いたくないのでしたら，

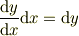
を公式だと思えばいいのです．(傾き×変位＝変化量，「全微分と偏微分との関係式」の常微分版)

裸の 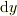, 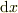という量がお嫌いでしたら

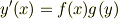
の両辺を 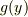で割り，その両辺を 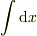で積分し，

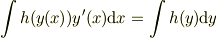
という媒介変数積分公式を使えば高校の範囲で解けますね． (見通しは悪いですが．．．)

裸の 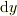, 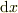といった表記は高校では使わないものですが，これは微分形式という考え方につながるので，是非理解して欲しいです．

kei さんのレス (2007/03/21(Wed) 11:27)

ＳＡＴＹさん，こんにちは

dy = f(x)g(y) dx

を微積分を使って理解するということですが，僕も既出の分までの 理解しかなくこれ以上の解説は出来ませんが

y = F(x)

に対して

y' = dF(x)/dx = F'(x)

は Fの微分 でなく Fの導関数 であり，fの微分は

dy = dF(x)/dx・dx…☆

で定義されえています．この式は微積分の専門書のどこかに載っているので 本屋さんや図書館で探してみてください． つまり，☆式はHiroさんもおっしゃっているように微積分の公式の一つです．

今，問題になっている式は

dy/dx=f(x)g(y) …◎

であって解が

y = F(x)…△

で得られたとしましょう．△式を◎式に代入して

dF(x)/dx=f(x)g(y)

が成立します．この式と☆式から

dy = dF(x)/dx・dx = f(x)g(y)・dx

が導かれます．微積の公式のみで出したことになりますが恐らく☆式

dy = dF(x)/dx・dx…☆

で詰まられると思うので簡単にですが証明を以下に示します．

y = F(x)に対してxが微小変化したときのFの変化量(微分)を

dy ≡ F(x+dx) - F(x)

で定義します．ここでdxは微小な値としましょう．すると

dy = F(x+dx) - F(x) = (F(x+dx) - F(x))/dx・dx←この段階でdxはただの数字です．

となって dx→0 としてやれば

(F(x+dx) - F(x))/dx→dF/dx

と書けるので dx→0 の下で

dy = dF(x)/dx・dx…☆

が導けることになります．最後のdxの効果で dy = 0 じゃあないのかと主張されてしまうかもしれないですが， dx→0 であっても dx = 0 でないので微小ながら0でない数字が最後に掛け算されているイメージです．

少しでも参考になればよいのですが．．．

ＳＡＴＹ さんのレス (2007/03/22(Thu) 09:06)

toorisugari no Hiro様， kei様ありがとうございます． dy=dy/dx・dx は理解することができたのですが，y'=f(x)g(y)がなぜ成立するのかわかりません．何度も大変申し訳ございませんが，教えていただければと思います．宜しくお願い致します．

ＳＡＴＹ さんのレス (2007/03/22(Thu) 11:11)

toorisugari no Hiro様， kei様 No.15038 の私の質問は間違いです．大変失礼致しました． ありがとうございました．