回転座標系について
回転座標系について
ZIG さんの書込 (2007/03/18(Sun) 00:15)
下のけんさんの記事に関連するのですが話題が違うので別スレを立てます.
慣性系(O系)に対して原点を共有し,角速度ベクトルωで回転運動する座標系(O'系)を考えた時, O 系でみたAの時間微分d A/dt,及びO'系でみたAの時間微分d'A/dtに対し, dA/dt=d'A/dt+ω×A が成り立つと言うことを軸に議論が展開されているようなのですが,この式はωが時間に依存するベクトルである場合にも成り立つのでしょうか. ωが定数であるときに関しては自力で↑を証明できるのですが,ωが時間変化する場合にはどうしても証明できません. 自分で色々試したのですが,ωの向きが変わらず大きさだけ変化する場合を考えても dA/dt=d'A/dt+{(ω+t*dω/dt)/w}(ω×A) のようになってしまいωが任意に変位する時に↑の等式が成り立つとは思えないのですが… どなたか↑の式の導出過程を教えていただけませんか?
Re: 回転座標系について
zoro さんのレス (2007/03/18(Sun) 12:23)
ZIGさん,始めまして.
初めに確認させてください.お書きになっているのは物理量Aはベクトル量ですか.そして,ω×Aは,ベクトルの外積ですか.
また,「dA/dt=d'A/dt+ω×A」の導出過程はどの本なりサイトでお知りになったのでしょうか? そこでは,どのような仮定の下に計算がされていましたか?
>ωの向きが変わらず大きさだけ変化する場合を考えても >dA/dt=d'A/dt+{(ω+t*dω/dt)/w}(ω×A)
とありますが,ωとwの違いはなにですか?また{(ω+t*dω/dt)/w}の部分はスカラですか?
質問ばかりで申し訳ありませんが,話が迷走するのは嫌なので,先に確認させていただきます,ご容赦ください.
なお,自分は「d'A/dt」の記法の真意を理解していないのと,昔自分で納得した形式をまだ再導出していません(式や図の表現を準備中)ですので,申し訳ありませんが,式自体を私は説明する気持ちはありません.
でも,自分で計算して深い理解に到達したいとするお考えには,敬意を表します.是非とも明快な結論に届かれると良いですね.
Re: 回転座標系について
zoro さんのレス (2007/03/18(Sun) 14:51)
簡単にコメントします.
この手の問題は,慣性座標系と回転座標系を明確に区別するところから始めます.そして成分と基底ベクトルとを注意深く時間微分し,特に回転座標系の基底座標が微分される時には,系の回転角速度による剛体回転を用います.この回転角速度の絶対値が時間依存性を持つようにしたいというのがご質問だと思います.
慌てて解くより前に,一度上に述べた座標系の記述を明確にすることが大切とおもいます.その為にも,えりさんへのコメントにも書きましたが,この数式掲示板で利用できる簡易LaTeXは,強力な式表現があるので練習して置くと善いと思います.
ベクトル演算というのは,あるいみ「プラ・モデル」ならぬ「数学模型」を作るようなものだと思います.最後の形だけで論議してもあまり意味はないと思います.途中の製作過程を知るには,自分で内部構造に手を出して確認しないと,模型の理解は進まないのだと思います.
Re: 回転座標系について
yama さんのレス (2007/03/18(Sun) 23:08)
ωが時間に依存する場合は,その時刻における角速度の値を用いるだけだと思います. すなわち,dA/dt=d'A/dt+ω(t)×Aです.
ところで,zoroさんは問題を難しく考えすぎていらっしゃるのではないでしょうか. 有限角度の回転を表すには,行列とか四元数とかを用いる必要があるでしょう. しかし微分係数を求めるだけなら,無限小回転についてだけ考えればよいので,ベクトルを用いて図形的に考えたのでよいと思います.
Re: 回転座標系について
zoro さんのレス (2007/03/19(Mon) 00:15)
>zoroさんは問題を難しく考えすぎていらっしゃるのではないでしょうか.
その可能性はあるかも知れません.回転系の座標については,きちんと時間微分をする事だけですが,恐らく初学者のばあい,慣性系と回転系のベクトル相互の関係と,基底ベクトルの処理とがごちゃ混ぜになって,とても変に解釈する恐れがあると思うだけです.
それに輪をかけて,d'A/dtという難しい記法では,何も説明した事にならないと思うからです.前回の時に,一度かなり説明文を書きましたが,こちらの掲示板では図も入れられず,解説式も時間とともに流れてしまうので取り下げました.現在は,別のところで判り易く書こうとしています.
もちろん,こちらのサイトで,自説を強く主張するつもりは在りません.ただ,dA/dt=d'A/dt+ω(t)×Aをいくら書いても質問者の方の理解が進んでいるように思えません.むしろ,このスレッドをお始めになったZIGさんも,この式を理解した上で,訳が判らなくなっていらっしゃるように感じます.
恐らく,私は,問題が「回転系でのベクトルの時間変化をどう求めるか」では無くて,「回転系での運動方程式をどう求めるか」であると思います.特に,地球の地表での運動を考える時に,回転系の運動方程式に,遠心力・コリオリ力を自然に導入する意味では,dA/dt=d'A/dt+ω(t)×Aだけで論議すると,誤解され易いと思います.
#私は,怠慢学生だったので,コリオリの力は運動方程式では知ってましたが, #地表での現象を実際に計算をした事が在りませんでした. #昨年,脚の運動を計算する準備で,ロボットの計算式の解説を見て, #地表のコリオリ力の導出を納得したぐらいです.
>ベクトルを用いて図形的に考えたのでよいと思います.
これに異論は在りませんが,回転系の基底ベクトルが, 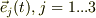 とした場合,
とした場合,
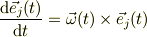
を式の上でと,傘型のチョコレート・モデルとで,両者の関係を納得できれば,と思います.でも,この理解がなかなかスムーズに行かないので,物理量としてのベクトルを慣性系と回転系とでスムーズにイメージできるようにするには,準備工作が必要と思います.
がしかし,それほどまで簡単にご説明できるとすれば,是非とも拝見して勉強させて戴きたいので,宜しくお願い致します.
Re: 回転座標系について
yama さんのレス (2007/03/19(Mon) 12:41)
質問者のZIGさんは,ωが定数のときに dA/dt=d'A/dt+ω×A が成り立つことは理解されていて,ωが時間に依存するときにも同じ関係が成り立つかどうかという疑問をお持ちなのだと思います.
それはたぶん回転中にωが変化することに引っかかっておられるのだと思います.
しかし微分係数に関係するのは無限小時間dtの間の変化だけです.時間dtの間にωがω+dωに変化しても,無限小変化dωはωに対して無視できるので,ωの値としては時刻tにおける値ω(t)だけを考えればよいことになります.
あるいは,無限小時間dtの間のベクトルの変化を表す式
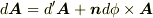 は
は 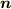 や
や  が時間に依存する場合にも成り立つので,この両辺をを
が時間に依存する場合にも成り立つので,この両辺をを 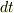 で割って
で割って 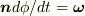 と置いてもいいでしょう.
と置いてもいいでしょう.
なお,d'A/dtという記法はdA/dtと区別するために用いられるものなので,区別できればこの記法にこだわることなく他の記法を用いてもよいと思います. また,dA/dt=d'A/dt+ω×A を基底ベクトルの間の関係に結び付けて考えるのも有益だと思いますが,この関係自体は基底ベクトルを用いなくても図形的に導くことができます.これについては,大抵の力学の本に書かれていると思いますのでそれを参照していただくのがよいと思います.
Re: 回転座標系について
けん(大学1年) さんのレス (2007/03/19(Mon) 14:25)
>yamaさん
>質問者のZIGさんは,ωが定数のときに dA/dt=d'A/dt+ω×A が成り立つことは理解されていて,ωが時間に依存するときにも同じ関係が成り立つかどうかという疑問をお持ちなのだと思います.
僕もそう思います.実際,教科書を読んでいたとき,僕も同じ疑問を持ちました.微小時間のωの変化を無視できるのであろうという推測できたため,とりあえずこの疑問は保留にしておき,ベクトル解析について知識がついてから再考しようと思っていました.詳しいことは分かりませんが,推測があたっていたようで安心しました.
>ZIGさん
初めまして.大学新2年のけんと申します.
dA/dt=d'A/dt+ω×Aの証明ですが,yamaさんの仰るように,たいていの大学の力学の本には載っています.その証明のどこかで,ωが一定でないときは成り立たないのではないかという疑問が出てきたら,また書き込みされるといいと思います.僕も一緒に勉強させてもらおうと思い,楽しみにしています.
回転座標系について
ZIG さんのレス (2007/03/20(Tue) 12:06)
微小時間のωの変化を無視できる,と言う事を認めれば確かにその通りなのですが
自分で行列を使ってかなり面倒な計算を徹夜でした結果,やはり
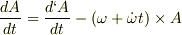 となりました.
この食い違いはどこから来るのでしょうか?
計算過程については後に掲載します.
とりあえず寝ます.
となりました.
この食い違いはどこから来るのでしょうか?
計算過程については後に掲載します.
とりあえず寝ます.
Re: 回転座標系について
ZIG さんのレス (2007/03/20(Tue) 12:09)
ちなみにωは角運動量を表すベクトル,Xはベクトルの外積です.
Re: 回転座標系について
yama さんのレス (2007/03/20(Tue) 14:00)
残念ながらZIGさんが導かれた式は正しくないと思います.
簡単のため, 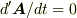 の場合を考えると
の場合を考えると
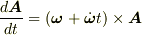 になりますね.(ZIGさんの式では右辺に-がつくことになりますが,たぶん誤記だと思います.)
この式で t=0 と置くと
になりますね.(ZIGさんの式では右辺に-がつくことになりますが,たぶん誤記だと思います.)
この式で t=0 と置くと
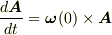 となります.これは,t=0 においては,
となります.これは,t=0 においては, 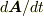 が,そのときの角速度
が,そのときの角速度 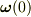 とベクトル
とベクトル 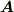 の外積に等しいことを示しています.
しかし,t=0 は任意にとることができる時間の原点であって,それ以上の特別な物理的意味を持つ時刻ではありません.従って t=0 で成り立つ関係は任意の時刻 t においても成り立つはずです.
すなわち
の外積に等しいことを示しています.
しかし,t=0 は任意にとることができる時間の原点であって,それ以上の特別な物理的意味を持つ時刻ではありません.従って t=0 で成り立つ関係は任意の時刻 t においても成り立つはずです.
すなわち 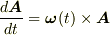 が成り立つはずです.
しかし,ZIGさんの式ではこれは成り立たないので,ZIGさんの式は正しいとは思えません.
が成り立つはずです.
しかし,ZIGさんの式ではこれは成り立たないので,ZIGさんの式は正しいとは思えません.
Re: 回転座標系について
zoro さんのレス (2007/03/20(Tue) 14:05)
ZIGさん,
どのように計算されているか判りませんが,自分で工夫をしながら計算をするのはとても良い経験になるとおもいます.
細かな話で申し訳ありませんが,ベクトルは; 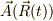 ,とか
,とか 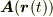 と書いた方が,一瞥しただけで如何にもヴェクタの姿に見えませんか?
と書いた方が,一瞥しただけで如何にもヴェクタの姿に見えませんか?
上記の書き方は;<Tex>vec A(vec R(t))</Tex>,とか <Tex>bm{A}(bm{r}(t))</Tex>とかとしています.
#この内,「bm」はこのサイト独特のマクロ定義だと思います.要は太字の指定. #Tex → tex とすれば表示に使えます.
>ちなみにωは角運動量を表すベクトル,
回転の角速度ベクトルとか,単に角速度ベクトルと言うべきだと思います.
角運動量は他の物理量になりますね.
この後に,説明の式を書いたのですが,エラーとなって書けません.
取り合えず,自分の感触を述べておきますと,回転角速度ヴェクタ 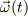 の時間微分が出てくるのは,時間微分が二次以上の場合です.時間の一次微分では,お書きになった式(このスレッドでの冒頭に書かれた式)が私の推定では合っていると思います.それ以上でも,それ以下でもありません.
の時間微分が出てくるのは,時間微分が二次以上の場合です.時間の一次微分では,お書きになった式(このスレッドでの冒頭に書かれた式)が私の推定では合っていると思います.それ以上でも,それ以下でもありません.
やはり,この式の使い方というか,理解が十分でないのだと思います.べつに難しい事は在りませんが,形式的に式を動かしていると混乱するのだと思います.yamaさんの様に,式を熟知されていれば,そのマンマだと思いますが.
私のお勧めは,変に一般論で細かく論議するよりも,位置ヴェクトルについての極座標表示にした場合について, ・北極星を+Z軸とした慣性系と,地球の自転ともに回転する回転系での位置ベクトルの定義を明らかにし, ・位置ヴェクトルの時間の1次微分としての速度ヴェクトル, ・速度ヴェクトル時間の1次微分としての加速度ヴェクトル,
を求めて見ると,イメージが明瞭になると思います.
こんなことは手計算する事もないかも知れませんが,一度納得しておけば,古典力学の95%ぐらいは自信をもって対応できると思いますよ(笑).
Re: 回転座標系について
余 さんのレス (2007/03/21(Wed) 04:00)
ベクトルとヴェクタとヴェクトルは,どういう基準で使い分けられているのでしょうか?
Re: 回転座標系について
zoro さんのレス (2007/03/21(Wed) 10:20)
【コフィ・ブレイク:ベクトルとヴェクタとヴェクトル】
結論を先に申し上げると,自分の脳内では;ベクトル=ヴェクタです.ヴェクトルは誤記でしょうね.
(背景説明)
私は,英語が苦手です.文法はもちろんの事,発音も苦手です.その上,辞書を引くのがおっくうでしたが,英辞郎を使うようになって,こまめに引くようになりました.さらに,音の出ないWindowsマシンの英辞郎第二版から,Macの英辞郎第三版にかえてから,クリックすると,発音が聞こえるのでとても面白く,単語を見たり,目をつぶりながらクリックして,同時発音をして遊んでいます.
#英辞郎第三版の音声は,合成音だろうと思いますが,自分のレベルでは十分と思います.
そこで,「綴り」,「発音」,「カタカナ表記」などの関連を見ていて,以前よりきになっていた,「ベクトル」を英辞郎第三版で見ると,ベクトル,ベクターの2つの記法がありました.
#「ベクター」は細胞操作などで使われるのだろうと思います.
ちなみに,「coffee」では,カフィー,コーヒー,コーフィなどの表示もあります.
#要は,「カタカナ表記での発音と綴りを少しでも近づけたらどうなるのか?」という試みですかね.
さて,使い分けですが; ・論議相手が「ベクトル」と書かれた場合:「ベクトル」で応答し ・自分からの説明で出る場合「ヴェクタ」と書きます
以上,このスレッドの質問からかけ離れた論議ですので,管理人さんの判定で,バツであれば,削除いたします.
Re: 回転座標系について
ZIG さんのレス (2007/03/21(Wed) 14:16)
yamaさんの言うようにt=0が一種の特異点になる事には私も違和感がありました. そこでもう一度計算式を整理して書き出した結果,私の間違いが分りました.
二種類の系におけるベクトルの関係を
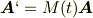
とおくと,
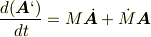
これを変形すると
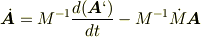
となって
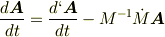
という式が出てきます.ここで私は今まで
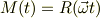
として計算していたので
(ただし 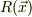 は
は 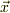 に垂直な面内で
に垂直な面内で 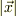 だけ回転する三次元回転を表す行列です.)
だけ回転する三次元回転を表す行列です.)
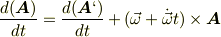
という結果が出ていました. 本来は
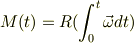
とするべきでした.こうすれば,

という正しい結果が出ます.なお, 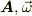 は両方とも三次元ベクトルであり
は両方とも三次元ベクトルであり  はベクトルの外積です.
はベクトルの外積です.
こういう間違いはやはりzeroさんの言うとおり形式的に式ばかりいじって,本質的な時間と運動の関係を失念しているところから来たものだと思います.
yamaさんzeroさん,けんさん,色々と指針を与えてくださって有難う御座います. Latexの扱いに戸惑って返信が非常に遅れてしまいました.申し訳ありません 上記の内容に誤り,突っ込み所がありましたら,又指摘して下さい.
>zeroさん ここの掲示板はどうやらlatexだけ書いた記事は撥ねるようです.
>けんさん 自分は大学新一年ですので後輩になります.これからもよろしくお願いします. (一浪なのでひょっとすると同い年かも)
Re: 回転座標系について
CO さんのレス (2007/03/21(Wed) 16:02)
本筋とは離れますが,一つ. > #この内,「bm」はこのサイト独特のマクロ定義だと思います.要は太字の指定. これは「このサイト独特のマクロ定義」ではなく, LaTeX で bm というパッケージを取り込むと使える命令です.
Re: 回転座標系について
けん(大学1年) さんのレス (2007/03/21(Wed) 23:53)
>ZIGさん
同い年ですね.新1年とはいってもすでに大学の内容を勉強されているようですが.こちらこそよろしくお願いします.
Re: 回転座標系について
zoro さんのレス (2007/03/22(Thu) 05:48)
ZIGさん,
難しい定式化のもとで計算されているようですね.私には判らないので,出来ればどのような本に準拠されているかをお教え下さいませんか?長い事,この手の計算をした事がないので,自分なりに計算を検証した後で,ぜひともZIGさんの方法も検証したいと思います.
#念の為に,位置ヴェクタについて,2次の微分を求めてみましたが,遠心力項とコリオリ力項が出てくるだけではないでしょうか. #ただし,回転系の方程式にすれば,慣性系で見えている力から,上記の2項を引く事になりますね. #まだ検証は足りませんが.
COさん,
>bm というパッケージを取り込むと使える命令です.
このパッケージで使える命令にはどのようなものが在るかを知るにはどうすれば良いかをご教示くださいますか?
また,他のパッケージはお使いになっていますか?もし宜しければ参考までにお教え下さると有難いです.
無題
ZIG さんのレス (2007/03/22(Thu) 14:19)
えっと,とりあえず私なりの計算の過程をもっと詳しく書くことにします.
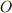 系に属するベクトル
系に属するベクトル 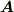 と
と 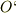 系に属するベクトル
系に属するベクトル 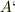 の関係が
の関係が 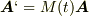 であるとします.
この関係式から,
であるとします.
この関係式から,
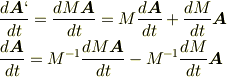
となります. で,ここの部分に関してはあまりよく理解していないのですが
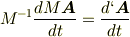
という解釈で以降進めます.
ここまでの作業は任意の一次変換行列 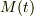 について成りたちます.
つぎに
について成りたちます.
つぎに 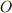 系に対して
系に対して 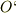 系が原点を共有して回転している場合
(原点を共有していないと一次変換では表現できないので.)
角速度ベクトル
系が原点を共有して回転している場合
(原点を共有していないと一次変換では表現できないので.)
角速度ベクトル 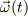 と
と 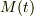 の関係を求めるには,(私はここで躓いていたのですが)
まず,
の関係を求めるには,(私はここで躓いていたのですが)
まず, 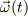 を時間で積分する事によって,時刻tにおいて時刻0の状態から
を時間で積分する事によって,時刻tにおいて時刻0の状態から 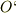 系がどの向きにどれくらい回転したかが分ります.
系がどの向きにどれくらい回転したかが分ります.
Re: 無題
zoro さんのレス (2007/03/22(Thu) 14:45)
あまり進むまえに,式の説明をしたほうがいいとおもいます.
式が判らないですが,少なくとも M(t) が説明なしに計算が進んでも,私には理解できません.
力学の基礎やベクトル解析の基礎をあまりにも飛ばしすぎても意味がないように思います.
ただし,ご自分で計算しようとされている点は,とても素晴らしいと思います.ぜひとも,ご自分の計算の前提を明確にしてください.たとえば, 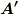 と
と 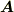 は何を表しているのでしょうか.
は何を表しているのでしょうか.
Re: テスト用掲示板
ZIG さんのレス (2007/03/22(Thu) 15:12)
すみません,まだ書いている途中で書き込んでしまいました.
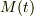 は時間に依存する,三次元ベクトルに作用する三行三列の行列です.
は時間に依存する,三次元ベクトルに作用する三行三列の行列です.
それで
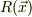 を
を 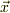 に垂直な面内で
に垂直な面内で 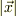 だけ回転する三次元回転を表す行列として定義し,これを使うと,上のほうで書いた様に
だけ回転する三次元回転を表す行列として定義し,これを使うと,上のほうで書いた様に
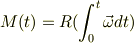
と言う風に表せます.
そして
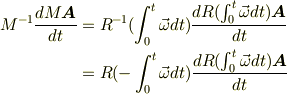
を計算して最終的に
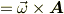
となるんですがこの過程の計算は煩雑すぎる上にlatexでの行列の扱いがまだ良く分っていないので割愛します.
無題
ZIG さんのレス (2007/03/22(Thu) 15:26)
ちなみに 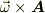 を導く計算ですが,
を導く計算ですが, 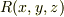 をyz,xz,xy平面内の回転行列に分解して成分表示し,それを又掛け合わせて
をyz,xz,xy平面内の回転行列に分解して成分表示し,それを又掛け合わせて 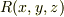 を求めて
を求めて 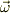 を成分で書き下して後はごり押しで計算しました.
を成分で書き下して後はごり押しで計算しました.
Re: 無題
zoro さんのレス (2007/03/22(Thu) 16:23)
ZIGさん,
良い意味で,頼もしい人だと思います.通常の枠組みから大きく外れていると思いますが,この馬力で頑張ってください.
私は,数学が苦手なので,行列を使ったベクトルの回転も得意でありません.通常,ある時間tにおける回転角速度ベクトルとの外積, 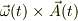 でのの幾何学的関係で納得してしまうのが大半だと思います.
でのの幾何学的関係で納得してしまうのが大半だと思います.
#ここら辺の説明はクロメルさんがどこかで書いていらしたように思います.
なお,回転運動は,並進運動と違って,ベクトルの成分を別々に適応すると違った結果になります.従って,あまり回転についての時間積分に拘ると話が混線する危険性があります.
お話の 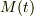 は回転を示すテンソル(テンサと書く場合も在り)だと思います.従って,ある時刻t=0でのベクトル(ヴェクタ)から,時刻tでの回転を求めるのだろうと推測します:
は回転を示すテンソル(テンサと書く場合も在り)だと思います.従って,ある時刻t=0でのベクトル(ヴェクタ)から,時刻tでの回転を求めるのだろうと推測します:
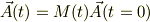
というのは,
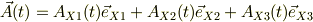
という空間ヴェクタが在るとき,
回転行列を;
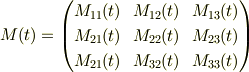
列ベクトルの表現を;
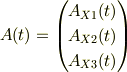
とした時に,行列と行ヴェクタの積;
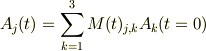
で与えられているといった感触ですか?
#なにかハイゼンベルグの行列力学などを思い出してしまう.
むしろ,これなら行列形式で計算を進めた方が良いかも知れませんが,式の意味を解釈するのが難しいと思います.
本来の問題に戻って,何を知りたくて,何を計算しているかを整理した方が良いと思います.回転系でのヴェクタでは,成分が時間依存性を持つだけでなく,基底ヴェクタが回転する事により時間依存性をもつ事ですよね.
ですから,簡単に,位置ヴェクタについて,慣性座標系, 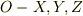 とそれに対する極座標系として回転座標系,
とそれに対する極座標系として回転座標系, 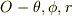 を考えた方が直裁ではないかと思います.
を考えた方が直裁ではないかと思います.
というのは,数学の弱いおじいさんの一意見でした.
なお,LaTeXの使い方は,書きながら聞いてしまえば良いですよね.むしろ本論;物理の解釈をドンドンと進めていただけると嬉しいですよ.
【追記】
回転行列を;
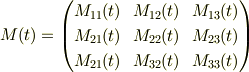
この原稿は;
<Tex> M(t) = begin{pmatrix} M_{11}(t) & M_{12}(t) & M_{13}(t) \ M_{21}(t) & M_{22}(t) & M_{23}(t) \ M_{21}(t) & M_{32}(t) & M_{33}(t) end{pmatrix} </Tex>
です.今後の為に.
回転行列と角速度ベクトル
toorisugari no Hiro さんのレス (2007/03/22(Thu) 19:16)
> 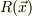 を
を 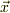 に垂直な面内で
に垂直な面内で 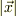 だけ回転する三次元回転を表す行列として定義し,これを使うと,上のほうで書いた様に
だけ回転する三次元回転を表す行列として定義し,これを使うと,上のほうで書いた様に 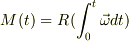 と言う風に表せます.
と言う風に表せます.
表せません.これができるのは 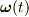 の方向が変化しない場合(2次元回転)のみです.
の方向が変化しない場合(2次元回転)のみです.
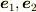 を平行ではない単位ベクトルとしたとき
を平行ではない単位ベクトルとしたとき

は0でありません.しかし,

は0です.ですから,
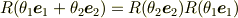
という式は一般に成り立ちません.( 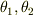 が微少量なら成り立ちますが....)
が微少量なら成り立ちますが....)
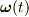 は
は  を固定すればベクトルとしての意味はありますが,積分した
を固定すればベクトルとしての意味はありますが,積分した 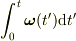 には一般にベクトルとしての意味はありません.yamaさんがおっしゃるように,微分の世界だけで考えた方が良いとおもいます.
には一般にベクトルとしての意味はありません.yamaさんがおっしゃるように,微分の世界だけで考えた方が良いとおもいます.
Re: 回転行列と角速度ベクトル
ZIG さんのレス (2007/03/22(Thu) 23:52)
zeroさん> Mの理解に関してはその通りです. テンソルと言うのは聞いたことはあるんですが,詳しくは知らないです. 基底ベクトルを意識した方が簡単になる,と言うのは確かにその通りだと思います. ベクトル図のを考える方法といっしょに試してみたいと思います.
hiroさん> 確かめます. ちょっと考えさせてください.
無題
ZIG さんのレス (2007/03/22(Thu) 23:54)
zeroさん> 有難うございます.つぎの機会に行列の書き方を試して見ます.
Re: 「フーコーの振り子」
zoro さんのレス (2007/03/23(Fri) 00:46)
ZIGさん,
私は最近,「木星のイオの公転周期の見かけの変動」を算出した事から,長い事無関心であった天文学にすこしく興味を持つようになりました.天文データも面白いですが,経度の測定,ティコブラーエの天文台の話,時計の歴史などゾロゾロと関連事項に触れる事になりました.
きのう,このスレッドの式を調べるべく図書館に行き,解析力学の本を探したのですが良いものが在りませんでした.そこで,天文学の本を見ていたら,
「フーコーの振り子」, アミール・D・アクゼル著,水谷純・訳, 早川書房,ISBN4-15-208680-7
という本を拝見し,借用してきました.レオン・フーコー(1819-1868)さんは1851年に花の都・パリで,振り子の実験をしたそうです.意外と新しいのに驚きました.
というのも,木星の衛星についてガリレオさんが観測し,時計に工夫をしたのは350年ほど前の事であったからです.当然のこととして「フーコーの振り子」は〜300年ほど前のことと思っていました.ところが,江戸時代後期の話だそうですね.
なんでこんな本のご紹介をしたかというと,ZIGさんのようにパワーのある人こそ,すこし廻りくどいような知識もあると,面白い展開になるのではなかろうかと感じたからです.
落ちこぼれた私が言うのも変ですが,物理を学ぶ上でも,ある種のバランス感覚が重要と思うようになりました.「全体の中の専門」とでも言えるかもしれません.
まあ,夏休みにでも一読されると良いかも知れませんね.カフィ・ブレイクとして,お許し下さい.
Re: 回転行列と角速度ベクトル
zoro さんのレス (2007/03/23(Fri) 09:22)
論議を元に戻します.
私が,ZIGさんの質問,元のけんさんの質問の;
(1) O 系でみたAの時間微分d A/dt,及びO'系でみたAの時間微分d'A/dtに対し, dA/dt=d'A/dt+ω×Aが成り立つと言うことを軸に議論が展開されているようなのですが,この式はωが時間に依存するベクトルである場合にも成り立つのでしょうか.
を私は納得できません.
敢えて,一般的なヴェクタAにしないで,位置ヴェクタに付いての時間微分を考える事にします.一般論はZIGさんが考察するべきだとおもうからです.
さて,慣性系での位置ヴェクトルを考えます.これは,ニュートンの運動方程式が,慣性系に対して記述される,時間に付いての微分方程式だからです.
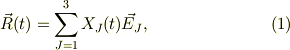
#ここで,慣性系の為に,基底ヴェクタ 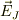 は時間変化をしません.
は時間変化をしません.
であり,「回転系の座標およびその基底ヴェクタ」が;
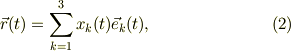
座標系の違いこそあれ,これらは位置ヴェクタですから,

ある時刻の時に,慣性系から見て,回転系が回転の角速度ベクタ 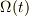 で回転しているとすれば,位置ヴェクタの表現と同様に
で回転しているとすれば,位置ヴェクタの表現と同様に
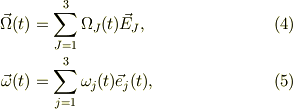
とした時に,

この回転角速度ヴェクタの幾何学的性質を用いると,回転系の基底ヴェクタの時間変化が与えられて;
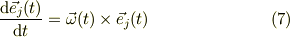
速度ヴェクタを考えます.式(1) より;
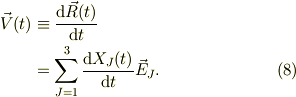
他方,式(2)からも同様にし,式(7)に留意して,
![\vec v(t) &\equiv \frac{\mathrm{d} \vec r(t)}{\mathrm{d} t}\\&= \sum_{j=1}^{3}\frac{\mathrm{d} x_{j}(t)\vec e_{j}(t)}{\mathrm{d} t},\\&= \sum_{j=1}^{3}\left(\frac{\mathrm{d} x_{j}(t)}{\mathrm{d} t}\vec e_{j}(t)+ x_{j}(t)\frac{\mathrm{d} \vec e_{j}(t)}{\mathrm{d} t}\right), \\&=\sum_{j=1}^{3}\left(\frac{\mathrm{d} x_{j}(t)}{\mathrm{d} t}\vec e_{j}(t)+ x_{j}(t)[\omega(t) \times \vec e_{j}(t)]\right),\\&=\sum_{j=1}^{3}\left(\frac{\mathrm{d} x_{j}(t)}{\mathrm{d} t}\vec e_{j}(t)\right)+\vec \omega(t) \times \vec r(t). \tag{9}](http://hooktail.maxwell.jp/bbslog/675335a8927a4dc4642749d6b8686036.png)
これが,少なくとも位置ヴェクタの時間微分の表現ではないでしょうか.単に,時間微分を丁寧に下だけです.その意味では, yamaさんのご指摘のような簡単なことだと思います.でも,「式が簡単なこと」と「その物理的意味を解釈しきって自在に,その式を使えること」には大きな差があると思います.
で,最後になりますが, d'A/dtに対応するものは;式 (9)の右辺の第一項だと推測します.そこで,新たに;
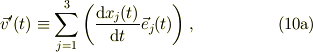
または,

を導入します.すると,速度ヴェクタについて;
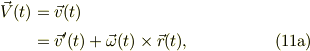
または,
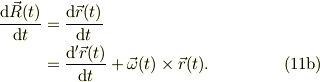
と書けると思います.こう書いて見てから,この式の意味を明確に解釈すれば,回転系の運動の持つ意味が明確になるのだと,私は思います.単にこの式(11)を天下り公式として操作すると間違えますね.
なお,2次微分は,丁寧に行えば出来ますが,式(11)の意味がはっきり判っていれば,一種の漸化式と考えて利用すればよいかもしれません.
====
しかし,このように考えるのは,運動方程式が時間微分で書かれていることに主眼をおいて考えるわけです.
別に,常に運動方程式を微分形式で表さないといけないわけではありませんね.例えば,力の線積分であるポテンシャルなどで運動方程式を立てたって言い訳です.
ですから,回転座標による逐次積分を考える事もあながち否定されるわけではないとおもいます.しかし,回転では,回転成分の順序によって状況がことなることは,高級な式で考えなくても判ることです.
例えば,本を手でもって回転させることをして見ます.あなたが回転系になった積りで動かしてください.
(1)本の表紙を表にして,左手で本の背表紙を持ちます.本は机の上に寝ているとします. (2)次に,本を「自分から見て手前に90°起こし」ます.本は机に垂直になり,表紙は自分を向いたままです. (3)次に,本を「自分から見て右に90°回転し」ます.本は表紙が手前で,背表紙が上を向いています.
今度は,また (1)に戻します. (2)'机に置いたまま,腕ごと「自分から見て右に90°回転し」ます.本は表紙が上を向いたままで,背表紙は自分から見て左,(1)の時の奥を向きます. (3)'本を「自分から見て手前に90°起こし」ます.本は机に垂直で,その背表紙は自分から見て左ですが,(1)の時の奥を向いたままです.
回転系で操作すると,同じ操作をしても順番が入れ替わると,結果が変わるわけですね.
(1)(2)(3)  (1)(2)'(3)'
(1)(2)'(3)'
ここらは数学的にどのように考えれば良いのか,私は知りません.じっくり検討されると良いですね.
まだ「新一年生 −ε」なのですから...:じっくり学んで,斬新にアイデアを練ってください.
Re: 回転行列と角速度ベクトル
zoro さんのレス (2007/03/23(Fri) 14:53)
ちょっと話が前に戻ります.そして以下の話は,あまり正確な話ではないので,流し読みしてください.
一般に任意の物理量であるヴェクタが,座標系, 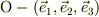 により,次のように表示されているとします.
により,次のように表示されているとします.
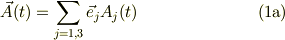
基底ヴェクタは直交規格化されているとします.

同様に他の座標系, 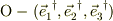 でも表示されているとします.
でも表示されているとします.
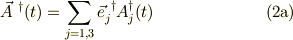
いま基底ヴェクタ 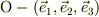 から
から 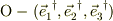 への回転行列を;
への回転行列を;
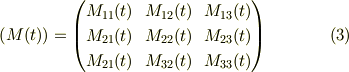
それぞれのヴェクタ成分で書いた列ヴェクタ,
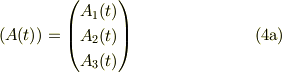
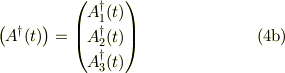
としますと,式(4a,b)は式(3)により関連付けられる;
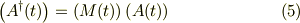
他方,それぞれの基底ヴェクタから作った行ヴェクタを;
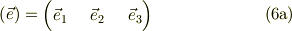
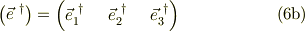
とします.するとこれらには,
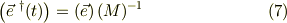
となります.これは,同一のヴェクタを単に異なる座標系で記述しているので,

事実,行・列表示から,通常のヴェクタに書き換えると;

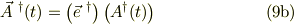
式(9b)に式(5,7)を適用すれば,式(9a)と一致しますね.(普通の説明の逆になっていますが)
多分,こんな関係をイメージしておけば,行列成分で,書いて,時間微分などを施せば,色々な関係式を出せるのでしょうが,更にスマートな方法を物理数学で習うでしょうから,あまり凝りすぎるのも考えものかと感じます.
Re: 回転行列と角速度ベクトル
Joh さんのレス (2007/03/23(Fri) 19:56)
zoroさん>
>回転系で操作すると,同じ操作をしても順番が入れ替わると,結果が変わるわけで>すね. >(1)(2)(3) (1)(2)'(3)'
有限回転ではそうですが,無限小回転ではこれがイコールになります.(回転の行列を A=E+εなどとおけば分かると思います.)それが,微分形で定式化する意味だと私は認識しております.
ところで,zoroさんのこだわっておられる,ヴェクタやテンサという表記について,個人的な要望を書かせてください.英語の発音に馴染むという意義は多いに認めますが,イギリス英語では,tensorはテンソーという感じですし,スコットランドでは,vectorはどちらかと言えばヴェクトルと発音します.coffeeは,イギリスではコーフィーと発音します.一口に英語と言っても,世界には色々な英語があり,ヨーロッパ域内ではまだまだイギリス英語が米語よりも好まれる場合も多いです.カタカナで,米語発音のようなものを無理して書くよりは,そこまで発音にこだわるならば,いっそのこと,英語のままで,vector, tensor, coffeeなどと書いていただけないでしょうか?それならば,人それぞれが,色々な読み方が出来ますので公平かと思います.(私は心の中でイギリス発音いたします.)アメリカがどうしても好きならば,その理由をお教えください. また,ベクトル,テンソル,コーヒーなどは,もはや日本語になっていますので,zoroさんが,いつも気にかけていらっしゃる,高校生や初学者の方が辞書を引く際の便宜などを考えれば,カタカナで書く場合には,慣用的な表記が良いのではないかと考えます. 私相手にならば,全文英語でのやり取りでも構いません.一度,ご考慮頂けますと幸いです.
Re: 回転行列と角速度ベクトル
zoro さんのレス (2007/03/23(Fri) 22:29)
Johさん,
>有限回転ではそうですが,無限小回転ではこれがイコールになります.(回転の行列を A=E+εなどとおけば分かると思います.)それが,微分形で定式化する意味だと私は認識しております.
私もそう思います.ZIGさんが回転を積分形で定式化されようと感じたので,一意的にならないという事例を挙げた訳です.むしろ量子力学での角運動量の非交換性につながるから,ちょっと先走って論議をしてみました.
>アメリカがどうしても好きならば,その理由をお教えください.
私が主として使っている辞書はほとんど米語発音のためです.特に最近は,英辞郎第三版の電子発音やカタカナ表記に近づけています.
>ベクトル,テンソル,コーヒーなどは,もはや日本語になっていますので
言葉は時代とともに変遷するものだとおもいます.文科省の物理や数学の用語辞典では「ベクトル」かもしれませんが,生物の遺伝子操作では「ベクター,ヴェクタ」といった書き方が多いとおもいます.←いまのところうろ覚え.
インターネットで検索してみると,図形描画の世界では,圧倒的に「ベクター・グラフィックス」ですね.「ヴェクター」は「ベクター」と同じ扱いのようです.「ヴェクタ」は極少数派のようです.PerlやJavaなどのプログラム関係の書をかかれていて数学も得意な方は「ヴェクタ」と書かれていました.
水泳の世界ではスカル(scull)という言葉があります.掌で翼動作をして揚力を利用して推進する手法です.それを示す場合,「スカーリング」と書かれる事が多いのです.3年ほど前に,これを知って,違和感を覚え,調べた所,ボート関係では「スカリング」がほとんどで,水泳では水泳協会のコーチ教本に「スカーリング」という記入が在りました.また,NKKのVTRや宣伝にも「スカーリング」とありました.当時,水泳のサイトでこの点を正すべきだろうという意見を出した所,強い否定を受けました.ところが,最近,NHKは「スカリング」に改訂しているようです.水泳のサイトでも徐々に「スカリング」が増えています.
必ずしもカタカナ表示が普及しても,それが固定的かというと,そんなに単純ではないと思います.勿論,文科省の検定図書などでは落とされるのでしょうが,民間人が自由に論議する場所では,自らが正しいと思う書き方で良いのではないでしょうか?
>全文英語でのやり取りでも構いません.
で,一体なにを論議するのですか?私には何も材料がありません.
Re: 回転行列と角速度ベクトル
Joh さんのレス (2007/03/23(Fri) 23:34)
ご回答ありがとうございました.
馴染みの無いアメリカ発音風のカタカナ語の理由は,お持ちの辞書が米語辞書だからなのですね.わかりました.できれば,もう少し,広い世界に目を向けて頂きたく思います.
言葉は常に変遷するものであるから(高校生や初学者の方が言葉の意味を調べるときに困るとしても),民間人は自分勝手な書き方をしても良いという理屈ですね.なるほど.それが自分の信じる書き方ならば,少なくとも我々民間人はどんな書き方をしても構わないわけですか.目から鱗が落ちました.私も,新奇なカタカナ語をどんどん創作していきたいと思います.
また,生物学でヴェクタと言う人達がいることが,物理や数学でもヴェクタと書いている理由なのですね.学際的でいらっしゃいますね.脱帽です.
私の言語感覚では,ベクトル,コーヒーなどは,もはや定着した日本語だと思っていたのですが,海外生活者の悲しさか,日本語の変化のスピードについていけていないのかも知れません.コーヒーがカフィに取って変わられる日も来るかも知れませんねぇ.しかし,カフィ・ブレイクはさすがに噴飯でした.
>で,一体なにを論議するのですか?私には何も材料がありません.
いえ,そんなに英語を正確に書きたいなら,いっそ英語で書いたらどうですか?という意味です.英語風のカタカナは,どうにも気障すぎてで,強い抵抗があります.しかし,これは個人的な感想ですから,論議をする気はございません.失礼いたしました.m(_ _)m
Re: 回転行列と角速度ベクトル
zoro さんのレス (2007/03/24(Sat) 00:26)
例えば,次のサイトでは,
「ベクター中間子の質量や分岐比の変化の検出」といった表現があります.
素粒子系では,もっと事例はあると思いますが,興味が無いので.ご自分で調べられると,物理でもベクトルばかりでない事がお分かりになると推定します.
航空機の世界でも,
の様な場合,なんと書くのでしょうか?やはり「スラストヴェクタリング」が素直だと思いますが,新聞とうでは「スラストベクタリング」でしょうね.すくなくとも「ベクトリング」にはならないでしょう.
また,英辞郎で「tensor」を見ると,「張筋」が先頭に出て来ます.これは肉単(ISBN4-86043-060-3)という本によると「大腿筋膜張筋(だいたいきんまくちょうきん)」と言って,歩行や走る際にまっすぐ前に足が出るのに重要だそうです.
Johさんはヨーロッパを所せましと活動されているのかも知れませんが,こと日本語の使われ方については,もうすこし柔軟であった方が良いかも知れませんね.
日本のTVの宣伝では「カフェ・オレ」は十分に伝達能力を持っているようです.
むしろ,近い将来「ベクトル」というと「ヴェクター」のこと?,て言われるかも知れませんよ.
管理人様:単語の話は,これで終わりにします.脱線をお許し下さい.
Re: 回転行列と角速度ベクトル
Joh さんのレス (2007/03/24(Sat) 03:52)
>すくなくとも「ベクトリング」にはならないでしょう.
当たり前ですね.
>日本のTVの宣伝では「カフェ・オレ」は十分に伝達能力を持っているようです.
カフェ・オ・レが,今の文脈に何の関係があるんですか???(まさか,カフェ・オ・レを英語だと思っていたとかw?)いえ,もう,これ以上揚げ足取りはしませんが,あまりにも見当違いな書き込みが続くので大いに笑わせていただきました.お礼申し上げます.(あ,ちゃんと最後に脱線って書いてあるんですね.)いやはやw
では,良い週末をお過ごし下さい♪