かず さんの書込 (2007/03/10(Sat) 13:36)

学部一年のかずです．（学科は物理です） 「統計力学その２」スレの一部をこちらに移しました．

１：確率モデルの等価性 統計力学には小正準集団，正準集団，大正準集団の3つの方法で現象を捉えることができますがどの方法をとっても結局同じ結果（すべてに当てはまるのかわかりませんが）が得られますよね．これは3つの方法が等価と言えるわけですがそのわけというか仕組みはどうなっているのでしょうか．

かず さんのレス (2007/03/10(Sat) 13:49)

連続レスで申し訳ありませんが，疑問に思ったことを少し追加します．

小正準集団のもとでは問題を解くときよく状態数→エントロピー→温度の定義式に代入→温度とエネルギーの関係式が得られる． ようにアプローチしますよね．でも途中まではエネルギー（ほぼ）一定のもとで考えていますがラストでエネルギーを変数として扱っているのはなんか不思議です．その結果得られた温度とエネルギーの関係式というのは温度を一定とみなせば正準集団になっている（温度が導入されているので見かけ上とまでしか言及できませんが）というのはさらに不可思議に思えます．

zoro さんのレス (2007/03/10(Sat) 21:49)

大昔，統計力学を捨てた者ですが，興味深く傍観しています．「小正準集団，正準集団，大正準集団」と書いてあっても何の事やらでした．

始めて勉強する方々に，判り易く，考え方を分析的に論議していただけると嬉しいです．ゆっくりでも，じっくりとお進め下さると，素敵だと思います．

takeo さんのレス (2007/03/10(Sat) 22:52)

小正準集団において，平衡状態を記述するパラメータは 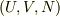です．

＞でも途中まではエネルギー（ほぼ）一定のもとで考えていますがラストでエネルギーを変数として扱っているのはなんか不思議です．

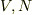（ は固定して）エネルギー の平衡状態を考えているわけなので，これは問題ないと思いますが？

気になるのは，小生準集団を定義したところでは，まだ温度は定義されていませんよね． ＞温度の定義式に代入 の温度の定義式とは，エントロピーのエネルギー微分の逆数を指しているのだと思います．これ自体は熱力学の関係式なので，論理的に言えば，正準集団で定義される温度と同じであるかどうかは微妙なところです

確率モデルの等価性についてですが， 例えば小正準集団と正準集団の等価性を考えて見ます．それぞれの平衡状態の記述の仕方は 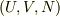と 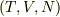です．こちら側が指定できるパラメータと言っていいと思います． 正準集団でいろいろな物理量を求めるとは，いろいろな物理量の集団平均を求めることを意味します．ということは 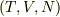以外の物理量は平均値であって「ゆらぎ」を持つことになります．エネルギーの平均値 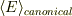もゆらぎを持っています．このゆらぎをちゃんと計算すると，マクロな系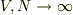（ ）でゼロになります．つまりエネルギーは一定値にゆらぎなしで決まる．このことを正準集団と小正準集団が等価であるというのだと思います． 逆に正準集団から始めて小正準集団と等価であることを示そうとする場合，温度の定義がエントロピーの微分で定義されているから当たり前すぎてどうしたらよいやら…

かず さんのレス (2007/03/11(Sun) 14:34)

takeoさん，zoroさんレスどうもです．

それとzoroさん， ＞大昔，統計力学を捨てた 理由なんかも教えていただけたら幸いです．もしかしたら統計力学を理解するうえで非常に重要な疑問や命題を含んでるかもしれませんから．

さて本題ですが，はじめに小正準集団においてエネルギーＥはパラメタとして指定できるので別に問題なかったです．（すいませんでした．） （余談ですが，小正準集団でエネルギーに幅を持たせているのはなぜでしょうか．）

正準集団と小正準集団の等価性について

ちょっと考えたんですが，正準集団というのは閉じた系の集団で環境（熱俗）を含めると孤立系，つまり小正準集団とみなせますよね．このとき，閉じた系は環境に比べて十分小さいのでエネルギーに揺らぎを持ちますが閉じた系を極限的に環境に近づける（十分大きくする）と閉じた系は孤立系に近似できて小正準集団となるということでいいでしょうか．（イメージ的には）

でも統計力学において粒子数は十分に大きいものとしていますが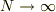（ ）体積（つまり系の大きさ）については何も要請していないはずです． ですから，正準集団と小正準集団は極限上，等価であるとしか言えないと思うんですが．

takeo さんのレス (2007/03/11(Sun) 17:20)

zoroさん，私も「なぜ，統計力学を捨てたか」に興味があります．よかったら教えてください．

＞統計力学において粒子数は十分に大きいものとしていますが，体積（つまり系の大きさ）については何も要請していないはずです． 「統計力学において」は言い過ぎだと思います．問題によって適宜要請するものだと思います． 統計力学としては粒子数も体積も特に要請はしていないが，統計力学によってマクロな系（熱力学的な系）を理解しようとするときにマクロな極限を要請するのではないかと思います．

正準集団と小正準集団の等価性についてのそのイメージが正しいかどうかですが， 断言することはできませんが，おそらくそのような感じでいいかと思います．私自身，あまり自信があるとは言えないので，下の参考書を勉強なさってはいかがですか？

＞余談ですが，小正準集団でエネルギーに幅を持たせているのはなぜでしょうか． 出版されている本で明確に答えている本は見たことがありません． 学習院大学の田崎先生のホームページ上で公開されている『統計力学』が非常に参考になります（さっき見たら完全版がでていました）．確率モデルの等価性についても詳しく解説があります（私もまだ読んでませんが）．出版されている『熱力学』も読むといっそう理解が深まると思います．

個人的な興味ですが（答えたくなければ結構です．） 学部一年生で統計力学をただ単にやっているだけでもすごいことですが，ここまで深く考えられているのは驚きです．統計力学が特別好きなのですか？もしくは他の，例えば量子力学も同じぐらい頑張っていらっしゃるのですか？

かず さんのレス (2007/03/11(Sun) 19:34)

＞学習院大学の田崎先生のホームページ上で公開されている『統計力学』が非常に参考になります（さっき見たら完全版がでていました）．確率モデルの等価性についても詳しく解説があります（私もまだ読んでませんが）．

田崎先生は熱力学の大家で有名ですし（まだ熱力学の教科書は持っていませんが），統計力学のノートは知ってました．少し前までちょうど確率モデルと相転移の章が未完成でしたが完全版が出てたんですね．みてみます．少し読んでからまたレスしたいと思います．

余談ですが，自分は量子力学，統計力学，一般相対論，場の理論と順繰りに手を付けてきたんですがやっぱり難しいですね．そのうち，量子力学と相対論は概念的なことは少しつかんだつもりです．場の理論はマジで難しいです．量子論も相対論も計算が煩雑なので（フーリエ解析とか）具体的な計算は2，3年の演習のときかなんかに後まわしにしようかと思っています．統計力学なんですが，煩雑な計算がわりと少なくまずこの分野をある程度やりこもうと思いました．

私自身もtakeoさんに興味があります．もしよかったら，簡単な自己紹介的なことを教えてください．

zoro さんのレス (2007/03/11(Sun) 21:05)

みなさん，

＞「なぜ，統計力学を捨てたか」

なんと言っても40年も前の事ですし，得意でなかったので記憶そのものが確かでありません．理化学事典(第3版)で，調べると

・カノニカル集合(canonical ensemble) ・大きなカノニカル集合(grand canonical ensemble)

という説明しか在りません．今回書き込む直接の原因となったのは「小正準集団」がとても奇妙に見えたからと思います．

学部1年の今頃は，電磁気学を一通りおわり，分子運動論にこっていました．これは，熱力学が頭に入らない反動で，純力学的に熱現象を理解したいという単純な動機でした．

統計力学も少し手を伸ばしたとおもいますが，カノニカル集合の離散的なエネルギ順位なるものがどのような系を対象としているかが判らなかったのが，その次のステップに進めない直接的な原因だと思います．

でも，その前に，熱力学の進み方，論議の仕方に頭が追従できず，そもそも温度の定義がすんなりしなかった事が大きな障害であったと推測します．

＝＝＝＝ そんな私が，最近，統計力学に少し興味を持ち出したのは，流体力学でおきる乱流現象を「時間・空間的な平均操作」する事で，特徴的な現象を抽出できるのではないかと感じているからです．これは，単なる数学的演算ではなく，背後に統計力学的なメカニズムがあるように感じる為です．

上の仮説はどこまで行けるか知りませんが，すくなくとも，このスレッドで統計力学を鑑賞させていただければと思いました．皆さんの論議，引用書籍・サイトなどとても面白いので，楽しみに傍観させていただきますね．

takeo さんのレス (2007/03/11(Sun) 22:59)

zoroさん，

＞流体力学でおきる乱流現象を「時間・空間的な平均操作」する事で，特徴的な現象を抽出できるのではないかと感じているからです．これは，単なる数学的演算ではなく，背後に統計力学的なメカニズムがあるように感じる為です．

これは，おもしろそうですね．私は，統計力学の広い汎用性に強く惹かれます．こんなことにも使えるのかって．

私も統計力学を学び始めたとき，古典物理とのギャップをものすごく感じました．量子力学がわかり，熱力学がわかってきたときに，統計力学もだんだんわかるようになってきたという感じです．

かずさん，

一般相対論，場の量子論にまで手を出されているとはまた驚きです． 私は学部三年ですが，量子力学と統計力学はまだ１年しか勉強していません．そのせいもあって，同じ目線での議論，大変勉強になりました．にわか知識にもかかわらず，興味があったので失礼させていただきました．

かず さんのレス (2007/03/12(Mon) 15:54)

zoroさんの発想は興味深いのですがそもそも乱流現象が何なのかわからないため何もコメントできなくてすいません．

ちなみに簡単に書くと 小正準集団＝micro canonical ensemble＝孤立系の統計方法 正準集団＝canonical ensemble＝閉じた系（エネルギーのやり取りあり）の統計方法 大正準集団＝grand canonical ensemble＝開いた系（粒子，エネルギーのやり取りあり）の統計方法

です．

takeoさん こちらこそいろいろ教えていただきありがとうございました．確率モデルの等価性についてですがテーマが重すぎたため，もう少し勉強してから出直してきます． 話が変わりますが（また別にスレを立てる必要があるかもしれません）

長岡本の統計力学p.70の正準分布（あるいは大正準分布）の導出過程で要となるのは の部分だと思うんですがここの議論があいまいな気がします．何か気づいたことがあったら教えてください．

zoro さんのレス (2007/03/12(Mon) 20:13)

takeoさん，かずさん，

私は，流体力学は意識して取りませんでした．で，今頃勉強しています．これは水泳の解析をしたいからです．人間の水泳では飛行機や船のように流線型の形状でなく，さらに比較的に強い加速運動をします．

ですから真っ当にぶつかると難しい事になります．飛行機より人間の動きの方が難しいとは思いもしませんでした．流線型の逆は「鈍い形状」で，円柱とか団扇のようなものを想像してください．それらが水の中を運動すると，その後方に渦ができます．ある程度ゆっくり動くとカルマン渦が出来，左右の渦が交互に出て行きます．運動速度が速まると，渦は非定常に多数発生し，物体の後方で「渦を巻き」ます．それこそ多数の渦がたむろする訳です．

その部分は「死水領域」とも言われています．しかし，プールやお風呂で観察すると，この「後方渦の領域」は，むしろ運動量と角運動量をもつ「水の塊」として運動体の後方にありながら，自発的に(あたかも自分の意志で動くかのように)運動体の後方に付いて来るのです．

通常の流体力学ではこんな領域があると飛行機は失速してしまうので，論議さえません．ところが，水泳では，このような「水の塊」の運動方程式が欲しい訳です．折しも，数学系の研究者では，このような乱流の数学構造がホットに論じられているようです．

私は，このような「水の塊」の運動の背景には，乱雑なるが故に持ちうる物理的運動構造を見いだすには統計力学的なアプローチが有効ではないかと推察するのです．

まあ，気長に勉強してみたいと思います．

＝＝＝＝ アンサンブルについて：

学習院大学の田崎さんのサイトを拝見しました．独自の解釈をされようとする熱意は伝わって来て面白いですね．

ご紹介の本を図書館で見て，ちょっぴり勉強したいとおもいました．

takeo さんのレス (2007/03/13(Tue) 00:04)

渦に関する解説，楽しく読ませていただきました．飛行機よりも人間の方が複雑な形をしているのは言うまでのことではないですが，実際言われてみると不思議です． 流体には疎い私ですが，機会があれば勉強したいと思いました．

＞長岡本の統計力学p.70の正準分布（あるいは大正準分布）の導出過程で要となるのは…

ですが，昔は大胆だと思いましたが，慣れてしまったようです（慣れは恐ろしいです）．一応論理は通っていると思います．

zoro さんのレス (2007/03/13(Tue) 01:31)

論議が進んでしまうと，お聞きするチャンスが無くなりそうなので質問させていただきます．

カノニカル・アンサンブル(本当は英語の方がイメージし易いのですが，「英語下手」が英語で書くのは気が引けるので)の導入部について，初心者に向けてじっくりと解説してある本としては何をお勧めになりますか？

すでに，【Re: 統計力学 かずさん， 2007/03/08(Thu) 19:09 No.14804】で，

>長岡先生の統計力学の本 ・統計力学，長岡 洋介 (著) ，岩波書店 (1994/07)，ISBN-10: 4000079271 >久保先生の演習書 ・大学演習 熱学・統計力学，久保 亮五 (著)，裳華房; 修訂版 (1998/09)，ISBN-10: 4785380322

ここでも，【Re: 統計力学その３かずさん，2007/03/11(Sun) 19:34 No.14877 】で，

>学習院大学の田崎先生のウェブ・サイト： ・「統計力学」 http://www.gakushuin.ac.jp/~881791/statbook/ でpdf入手可．

のご紹介がありました．

できれば，これから統計力学を始める新人の方や，再復習したいOBの方に向けて，良い参考書，演習書，ウェブ・サイトのご紹介をいただけると嬉しいです．

ちょっと脱線気味ですが，お許し下さい．

zoro さんのレス (2007/03/13(Tue) 04:03)

自己コメントです．

上の田崎さんの統計力学のpdfの導入部を拝見しました．40年前に，砂川さんの理論電磁気学を拝見した時の熱気を見た気がします．これは，自分に取って運命的な出会いをさせていただいたように思います．

この歳で，再勉強する分野が複数になってしまい，何処まで進めるか疑問ではありますが，このpdfに沿って勉強する事にしました．

少なくとも，先に書いた質問は撤回します．デッドロックに衝突したら質問に来ます．勿論，このスレッドは，引き続き，傍観させていただきます．

かず さんのレス (2007/03/13(Tue) 12:43)

takeoさん，正準分布の導出過程についてはなんとなく解決しました．迷惑かけてすいません．

zoroさん，察するにご年配のようであられますが再勉強する気が湧き上がり，その気力が凄まじいのに頭が上がりません．なかなかできるものではないと思っています．ぜひとも続けてください． ちなみに先ほどの教科書，参考書はほぼ定番といわれるものです．この2冊をマスターしたら学部レベルの統計力学は身についた（十分すぎる？）といっていいはずです． 田崎先生の統計力学はまもなく出版すると書いてありますのでおそらく統計力学の教科書に革命を与える本（熱力学のように）になるものと思われます．

zoro さんのレス (2007/03/13(Tue) 17:35)

かずさん，

>統計力学の教科書に革命を与える本（熱力学のように）になるものと思われます．

なるほど，熱力学の目次だけ拝見しましたが，素人目にも，工夫が凝らされているように感じます．

以前，音楽の話で，ドイツの音楽が飛躍的に向上したのは，J.S.バッハがイタリア留学から帰り，楽譜をドイツ語で書くようになった頃からだといった解説を見たように思います．我が国は古くから，アジア諸国から文化の流入をうけ，それを我が国の言葉にかえて表現するようになって，段々と我が国の独自文化を醸造したのだろうと思います．

江戸後期から段々と西洋文化としての数学・物理を導入して来た我が国も，いよいよ独自の数学・物理の文化を構築するようになりつつあると思います．自分の目・指・頭で作り出す解説書を「広い意味での読者」が応援できるといいですね．

また，田崎さんのサイトを拝見していると，

・数学：物理を学び楽しむために

• http://www.gakushuin.ac.jp/~881791/mathbook/index.html

と言うのがありました．これは物理数学をほどほどに，バランスよく解説しているので，この数式掲示板でも引用するのに好適かも知れません．

いずれにしろ，素人が再勉強する良い資料の一つだなと思いました．

以上で，私の出番は終了とさせて戴きます．まさに，老いて子に教えられ，でした．

takeo さんのレス (2007/03/13(Tue) 17:59)

もう一つ私がときどき参考にする教科書としては 川村光さんの「統計物理」があります．これは，臨界現象の物理についても比較的丁寧に書かれています． 高橋康さんの教科書も少し変わっていますが，良かったと思います． あとは，小田垣さんの教科書は簡潔なものを好む人にはいいかもしれません． しかし，どれも一長一短でこれ！という決定版は私には見つかりませんでした．

やはり田崎先生の統計力学で勉強されるのが一番だと思います．中でも第２章と第４章は，他の教科書ではあやふやに扱われていることが明確に書かれています．他の教科書で勉強していてはなかなか理解できることではないと思います（少なくとも私には一生かかっても理解できないところでした）．まさに革命的な本になること間違いなしでしょう． 前にも書きましたが「熱力学」も読まれると，統計力学がいっそう楽しく勉強できると思います．是非併せてお読みください．

このスレッドはこれで完結でしょうか． 私も統計力学の後半部分を読んでみてから，確率モデルの等価性について質問に来ようと思います．

zoro さんのレス (2007/03/13(Tue) 18:27)

takeoさん，

>前にも書きましたが「熱力学」も読まれると，統計力学がいっそう楽しく勉強できると思います．是非併せてお読みください．

はい，実は，このサイトに来てから，「熱力学の関係式で全微分が出来る事の重要性」に気づき，「これなら熱力学を見直せば判るのかな？」と思っていたのです．

先ほど田崎さんの「熱力学」の説明ページを拝見して，内心この本の流れなら購入しようかなと思っていました．ついでに流体力学の項でも付け加えていただけれると面白いですが(笑)．

研究者が独創的な解説書をお書きになるのと同時平行して，今回のスレッドのように学生さん達が独創的な解釈を論ずるのも大切と思います．現代の通信事情の発展は，従来では思いもしなかった相互作用を「物理の勉強」にも提供してくれているのでしょうね．当分はスペクテイタで拝見していますから，ドンドンと論議をしてくださいませ．