のり さんの書込 (2007/03/09(Fri) 20:49)

はじめましてこんばんわ． 教えて下さい． １枚の板があるとした時，その板の反り具合を計算式から求めたいのですがどのような計算式になりますか？ 測定する点は３点になります．表面・裏面，計６点です．いろいろ調べて見ましたがわかりません・・・ そもそも表面・裏面の３点ずつを見るだけでその板のそりがわかるのでしょうか？ すみませんが教えて下さい．お願いします．

CO さんのレス (2007/03/10(Sat) 00:55)

のりさん，初めまして．

> 測定する点は３点になります．表面・裏面，計６点です．

３点の何を測るのですか？ 学校の課題か何かで，この問題を解こうとしているのでしょうか？

のり さんのレス (2007/03/10(Sat) 09:55)

おはようございます． 返信ありがとうございます． すみません，学校の課題で自分で題を考える物です．

３点で板のそれぞれの位置での距離を測定します． 測定する位置はどこでも良いのですが私なりに考えましたところ三角形で結べる位置で測定した方が良いのかと思いました． しかし，両面から測定しようと考えているのでそしたら横一列の方が良いのかと思いました．

すみませんがご意見お願いいたします．

CO さんのレス (2007/03/10(Sat) 10:12)

おはようございます，のりさん．

とても面白い問題ですね． 私も解答を持ち合わせているわけではないですが，一緒に考えてみたいです．

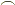「そり」として考える形は か だけで良いでしょうか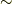？ ( とかいうのは考えますか？)

工業分野では「そり」の定義が既にあるのかもしれませんけれども， 自分で考えてみるのは面白そうですね． :)

のり さんのレス (2007/03/10(Sat) 10:40)

返信ありがとうございます． 何にしようか考えていたらふと思いつきました． そうですね，そりで考えているものは⌒のようなそりを想像しています．〜と言う考えも面白そうですね．⌒の題をクリアしたら考えたいですね．

板というか円盤みたいなそりを考えるとしたら円盤の1周をすごく細かく分割して測定していけばおのずと反っているとわかると思いますがそれではなくある何点かの位置の測定結果から全体の反りを計算できるのかなと考えました． 表面だけの測定だと厚みの違いが出てきてしまうのかと思い，両面測定を考えました． どうでしょうか？

CO さんのレス (2007/03/11(Sun) 06:38)

> ３点で板のそれぞれの位置での距離を測定します．

距離の測定の仕方はどうしますか？ たとえば板の表面に３点 A, B, C をとるとして，AB間の距離はどうやって定義していますか．

たとえば，

1. 伸びない糸を用意する
2. 糸の 0 となる基準点を A 点にピンでとめる

このあと，

3a) B点まで糸をピンと張って，B点の位置を糸上に記録する ( 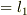) 3b) B点まで板上を糸を這わせて，最短となる経路をとったときの B 点の位置を糸状に記録する ( )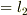

そして，

4. 糸をはずして基準点から糸上に記録された点までを定規で測る

という方法が考えられます．3a)，3b) に対応して，二つの距離が定義できると思います．

3a),3b) 両方の方法で測っておくと，もし 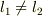ならば，その板は反っていることになると思います． まあ，糸をピンと張ったときに隙間ができていれば反っているということはすぐにわかりますが． 上記の方法でそれを定量化できないかなぁ．

> 表面だけの測定だと厚みの違いが出てきてしまう

とりあえずまずは問題を簡単にするために，板に厚みはないとして考えてはどうでしょうか．

CO さんのレス (2007/03/11(Sun) 06:49)

上の 3b) の方法で，板の表の A,B 点に対応する真裏の点 A',B' 間の距離( 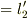)も測定したとします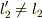． ならば，やはり板は反っていると言えそうですね． この場合は板に一様な厚みがあるとしないとダメですが．

のり さんのレス (2007/03/11(Sun) 19:46)

返信ありがとうございます． 確かに面に対して横にから測定する方法を考えましたが今，思っている測定の方法は面に対して垂直に測定して，面から垂直である一定の距離までを３箇所測定しましてその測定値からそりを割り出そうと考えていました． そうですね．まずは厚みは置いといてそりだけに集中します．

CO さんのレス (2007/03/12(Mon) 16:27)

> 今，思っている測定の方法は面に対して垂直に測定して， > 面から垂直である一定の距離までを３箇所測定しましてその測定値からそりを割り出そう

測定の仕方がうまく想像できないのですが，もしまとまったら また書き込んでください．楽しみにしています :)

トンガリ さんのレス (2007/03/12(Mon) 18:15)

ＪＩＳによれば 【平面度の定義】平面度とは，平面部分の幾何学的平面からの狂いの大きさをいう． 【平面度の表示】平面度は，平面部分を互いに平行な二つの幾何学的平面で挟んだとき， それら両平面の間隔で表し，平面度____mm又は平面度____μmと表示する．

【平面の平行度の定義】平面の平行度とは，一方の平面を基準平面として， この基準平面に対して平行な幾何学的平面からの他方の平面部分の狂いの大きさをいう． 【平面の平面度の標示】平面の平行度は，基準平面に平行な二つの幾何学的平面で その平面部分を挟んだとき，両平面の間隔が最小となる場合の両平面の間隔で表し， 平行度____mm又は平行度____μmと表示する．

これ等の測定で，三点測定とは聞いたことがない，安定支持のための三点支持はよく聞く． そうだ，レンズの曲率半径を測る古典的な道具は球指と呼んで三点支持だ．オチョクラレタかな・・・

幾何学的平面の代用として，測定物より大きな石定盤を用い，その上に測定物を載せる． この場合，石定盤に載せられた測定物は安定していること．すなわち三点支持が自然に行われること． 石定盤と測定物の裏面との最大スキマが【裏面の平面度】であるが，裏側なので測定は容易でない．

板厚一定と仮定して表て面を測るとか，板厚と表て面を各所で測るとか，工夫が必要です． 測定する個所数が正確さの条件ではありません．スキマの最大値を得さえすれば十分です． 直感的に最大スキマの場所を発見できなければ，何個所か測定して見つける必要が出てくる．

これ等の測定に式などなく，最大スキマとか両平面の間隔が最小の概念である．

のり さんのレス (2007/03/13(Tue) 09:36)

返信ありがとうございます． 測定方法は頭の中では絵に浮かんでいるのですがうまく言えないですね． 私が考えている測定方法を整理すると， まず，測定対象物はＣＤです． 測定方法はＣＤを縦にして，ＣＤからある規定値までの距離を測定します． 表面で３箇所，裏面で３箇所でこの３箇所というのは測定する点がＣＤ上で三角形になる用な位置を測定しようと考えています． 表面・裏面全く同じ位置の測定を考えています．

トンガリさん． 平面の反りを測定するのに，計算式はいらないのですか？ 測定する箇所の距離を測定・比較すればそりがわかってしまうんでしょうか？

トンガリ さんのレス (2007/03/13(Tue) 11:19)

質問の【平面の反り】の定義は何ですか?????，私は先に常識的に【平面度】と解釈しました． ところが違う様です．もしかしたら，ＣＤが皿バネ状とかパラボラアンテナ状に反っているとか， ウエーブ座金状に反っているとか，数少ない測定値から全体像を補間式で表したいのか知らん・・・

あるいは，リング状の一つのトラックのウエーブ状の反りを式で表現したいのか知らん． 表現したいのがトラックのウエーブ状の反りだとしたらフーリエ解析が第一の候補でしょう．

ＣＤの場合は製造原理から厚さは一定に出来上がるので，また片面しか記録に使用しないので， 裏表同一場所の測定の片方はムダだと思います．他に測定するべき場所があるだろうに・・・

仮にＣＤを支持具で3点支持して，その支持点の反対側を3個所測定したとしたら，それは ＣＤを測っていると言うより，支持具を確認しているに過ぎず，何も測ってないのに等しい．

片面の有効な3個の測定値だけではＣＤの基準平面の傾きを大雑把に推定できるだけで， 高次の反りを把握できるハズもないのは誰の目にも明白だ ｍ(＿ ＿)ｍ ．