振子

地球の自転の角速度をωとします．北緯αの地点では，回転座標系から見ますと，振子の回転周期は 2π/ωsinα です．これは地球の自転周期2π/ωより大きく，回転座標系では1日経ったときに振子の振動面が変わっているということを表します． 1日後，振子はもとの場所に戻ってきています．ですが，回転座標系では振子の振動面が異なっています．1日前と同じ場所で観測して振子の振動面が変わっているのに，静止系で見れば振動面が同じに見えるのですか？

Re: 振子

山旅人さんのレス (2007/03/08(Thu) 22:50)

> 1日後，振子はもとの場所に戻ってきています．

いいえ，戻らないでしょ．お書きの通り，振動面の回転周期は 2π/ωsinα です．「戻ってきている」と思うわけは何ですか？

Re: 振子

けん（大学1年）さんのレス (2007/03/08(Thu) 23:11)

すみません，戻ってきているというのは，振子ではなく，振子をつるす固定点でした． 1日後に同じ場所にある固定点に対し，振動面の回転周期2π/ωsinαのため，振子は同じ振動面にはありません．これは回転座標系では1日経ったときに振子の振動面が変わっているということを表します．静止系から見ても，振動面が変わっていることになります．同じ位置にある固定点に対して回転座標系では振動面が変わっているのですから．

Re: 振子

山旅人さんのレス (2007/03/08(Thu) 23:21)

> 静止系から見ても，振動面が変わっていることになります．…(#) いいえ，静止系から見ると，振動面は変わっていません．

> 同じ位置にある固定点に対して回転座標系では振動面が変わっているのですから．

これは，(#) の根拠にはなりません．振子の振動面は，観測地点（回転系）での鉛直軸の回りに回転するのです．

Re: 振子

山旅人さんのレス (2007/03/08(Thu) 23:41)

そうか，わかりました．けんさんは，地軸のまわりの回転を考えておられるのですね．その場合には，振動面の回転周期は，2π/ω です．すなわち，もとに戻ります．周期 2π/ωsinα は，観測地点（回転系）での鉛直軸のに対する回転周期 です．

すいません，以降は明夜に．

Re: 振子

けん（大学1年）さんのレス (2007/03/09(Fri) 00:17)

地軸のまわりの振動面の回転の周期と，観測地点（回転系）での鉛直軸に対する回転の周期は違うのですか？

では，回転座標系は，1日前の座標系とは重ならず，ずれているのでしょうか？1日で元のところに戻ってくるのだから，重なるかと思っていたのですが…．

Re: 振子

山旅人さんのレス (2007/03/09(Fri) 18:29)

すいません，ひとつ上の私の書き込み No.14814 をそっくり削除（撤回）させてください．その上の No.14813 は残します．変に勘違いをしてとんでもないことを書き込んでしまいました．

けんさん，混乱させてしまい申し訳ありませんでした．続きは，後刻 or 明日に…

Re: 振子

けん（大学1年）さんのレス (2007/03/11(Sun) 18:10)

地軸のまわりの振動面の回転の周期と，観測地点（回転系）での鉛直軸に対する回転の周期が違うかどうかが分かりません．

またお願いします．

Re: 振子

山旅人さんのレス (2007/03/11(Sun) 23:06)

けんさん，レスを書かずに申し訳ありません．今日まで，フーコー振子についてはよくわかっていると思い込んでおりまして，思わず書き込んでしまいました．お尋ねに回答しようとよくよく考え直してみると，自分自身がこの問題をきちんと回答しきれるほど理解していないことに気づかされました．で，この問題に対し，自分自身が納得できる回答を得た時点で再度書き込ませていただきます．

（地軸を軸とする）緯度 α の緯線に接する円錐の側面を展開した扇形の中心角は，2πsinα ですね．

Re: 振子

yama さんのレス (2007/03/12(Mon) 00:11)

振子の振動面は，鉛直軸のまわりを回転するのであって，地軸のまわりを回転するわけではありません．地面に固定した座標系は地軸のまわりを１日の周期で１回転します．地軸と鉛直軸を含む平面内で，この角速度ベクトル 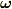$\bm{\omega}$ を鉛直方向と水平方向に分解すると，鉛直方向の成分が ωsinα，水平方向の成分が ωcosα になります．従って鉛直方向の成分 ωsinα が振子の振動面の回転の角速度になります．水平方向の成分 ωcosα は，水平軸のまわりの鉛直軸の回転の角速度であって，振動面の回転には関係しません．

Re: 振子

けん（大学1年）さんのレス (2007/03/12(Mon) 16:58)

解説ありがとうございます．

北緯αの地点では，回転座標系から見ますと，振子の回転周期は 2π/ωsinα です．これは地球の自転周期2π/ωより大きく，回転座標系では1日経ったときに振子の振動面が変わっているということを表します． 1日後，振子はもとの場所に戻ってきています．ですが，回転座標系では振子の振動面が異なっています．1日前と同じ場所で観測して振子の振動面が変わっているということが，静止系から見て振動面が変わっているということの理由です．

それから，水平方向の成分ωcosαには何か別のものに寄与するのですか？

Re: 振子

ｙama さんのレス (2007/03/12(Mon) 17:42)

空気抵抗などが無視できるとすれば，慣性系において振子にはたらく力は重力と糸の張力だけです．しかし，支点が地球とともに回転するので，支点とつながれた糸の張力によって振子も回転します．回転に伴って重力の方向も変化します．その結果慣性系から見ても振動面が変化することになります．なお，慣性系から見た振子の運動は，単純な振動ではなく振動しながら円運動することになります．

>それから，水平方向の成分ωcosαには何か別のものに寄与するのですか？

これは既に書いたように鉛直軸の回転に関係します．地球が地軸のまわりに微小角 dφ だけ回転したとすると，鉛直軸は cosαdφ だけ回転します．これは初めの鉛直軸と回転後の鉛直軸がcosαdφの角度で地球の中心で交わることから分かると思います．

Re: 振子

けん（大学1年）さんのレス (2007/03/12(Mon) 19:03)

＞従って鉛直方向の成分 ωsinα が振子の振動面の回転の角速度になります．

鉛直方向だから振子の振動面の回転の角速度っていうのは，明らかなものなんでしょうか？よく分からないのですが…．

＞なお，慣性系から見た振子の運動は，単純な振動ではなく振動しながら円運動することになります．

これは数式で解析できるんでしょうか？

Re: 振子

yama さんのレス (2007/03/12(Mon) 22:25)

振子は鉛直軸を含む面内で振動します．従って，振動面が回転するとしても振動面は常に鉛直軸を含んでいなければなりません．その場合に可能な回転は鉛直軸のまわりの回転だけです．

慣性系から見ると支点が円運動していて，その支点から吊された振子が振動するので，振子は振動しながら円運動することになります．その運動を数式で解析することもできるでしょうが，慣性系での運動方程式を直接解くのは計算がかなり面倒なものになりそうです．

Re: 振子

山旅人さんのレス (2007/03/13(Tue) 00:01)

>> やまさんいつもいつも有難うございます．解説を読ませていただき，私自身の混乱と頓挫の原因がわかりました．

> 振子の振動面は，鉛直軸のまわりを回転するのであって，地軸のまわりを回転するわけではありません．
> 従って鉛直方向の成分 ωsinα が振子の振動面の回転の角速度になります．
> 水平方向の成分 ωcosα は，水平軸のまわりの鉛直軸の回転の角速度であって，振動面の回転には関係しません．

赤道上（α＝0）では，鉛直成分 ωsinα＝0 が振子の振動面の回転の角速度で，鉛直軸のまわりを回転せず，水平成分 ωcosα＝ω で 鉛直軸が，（地軸のまわりを） 回転する．

これでは，「振動面が地軸の回りを回転する」と誤解してしまっても無理もなくはありません…？← 自己弁護！

Re: 振子

けん（大学1年）さんのレス (2007/03/13(Tue) 16:33)

おかげさまで理解できました．ありがとうございました．

[home] [掲示板] [ページの先頭]