かず さんの書込 (2007/03/06(Tue) 20:40)

初めて質問します．（返信はすでにしましたが）物理所属の学部一年のものです． 統計力学を勉強していてふと思ったのですが，

エントロピー増大の法則は統計力学において基礎原理なのでしょうか． それとエントロピー増大の法則を基礎原理として自由エネルギー最小の原理が導かれえるのでしょうか（つまりこれらは等価であるのか）

これらの応用先として相転移の問題の中でイジング模型がありますがエントロピー増大の法則を用いても解けるでしょうか．（つまりミクロ正準集団として）

クロメル さんのレス (2007/03/06(Tue) 23:26)

初めまして，かずさん．

統計力学では，エントロピー増大の法則は基礎原理ではないと思います．

そのかわり，統計力学で大事な基礎原理は，どの状態も等しい確率で実現するという等重率の原理です．これは，一次元の系では証明できますが，一般の場合は証明できていません．これを仮定した上で（この原理の仮定をエルゴード仮説と呼ぶ），状態を表すパラメータがどの値をとる時，最大の確率をとるかを考え，その最大の確率をとるパラメータを持つ状態が実現するというのが統計力学の基本姿勢だと思います．統計力学でやっていることは統計・確率論です．

統計力学では状態数Ωの対数にボルツマン定数をかけたものｋｌｎΩが，エントロピーに相当するものとして出てきます．これが熱力学で定義されたエントロピーS_tと一致するというのが，ボルツマンの関係式S_t=ｋｌｎΩ（≡S_s）です．これは統計力学的エントロピーS_sの定義になっていますが，熱力学的エントロピーS_tの定義式でないことに注意してください．多くの本では同一視して両方ともＳで書かれています． エントロピー増大の法則については，統計力学では確率的にほぼ確実に成り立つといえます．

takeo さんのレス (2007/03/06(Tue) 23:44)

かずさん 一次元イジング模型は状態数を数えることによって，ミクロ正準集団として解けます． よくわかりませんが，エントロピー増大の法則＝ミクロ正準集団という認識ですか？

クロメルさん，はじめまして．

＞エントロピー増大の法則については，統計力学では確率的にほぼ確実に成り立つといえます．

とはどういうことなのかよくわかりません．"ほぼ"というのも気になります．詳しく教えてくださいませんか．

クロメル さんのレス (2007/03/06(Tue) 23:58)

調べていて疑問に思ったことなんですが，自由エネルギー最小の原理でなぜ「原理」というのかが，よくわかりませんでした．私の読んだ本にも原理と書いてありました．原理とは，「他のものがそれに依存する本源的なもの」と辞書にあります．

しかし，私が見た限りでは，統計力学的には等重率の原理から確率論によって導かれる定理と呼んだほうがいいもののように思えました．熱力学では「原理」ということなんでしょうか？

クロメル さんのレス (2007/03/07(Wed) 00:19)

takeoさん，初めまして．

エントロピーがほぼ確実に増大することについて説明します．

例えば，二つの系を接触させた時，二つの系へのエネルギーの分配方法は，エントロピー，つまり状態数を最大にするように分配されますよね．これは，等重率の原理から，状態数が大きいほどそのエネルギー分配をとる確率が大きいということです．他のエネルギー分配は状態数が少ないですが，起きる確率はゼロではない（しかし，限りなくゼロに近い）と考えます．こうして系は確率的に熱平衡状態に近づきますが，ここで，非常にミクロな動きとしては，低温側から高温側へエネルギーが動くことは確率論では起こらないとはいえないということから，「ほぼ確実に」という表現をしました．

takeo さんのレス (2007/03/07(Wed) 00:21)

歴史的な経緯から適当でないにも関わらず「原理」となっていることはよくありますが，この場合はどうなんでしょうね． 例えば，最小作用の原理を基本的な原理として力学を定式化することができるように，物理において変分原理は本質的な事だからではないでしょうか． といっても，自由エネルギーの最小の原理から出発した熱力学を知りません．普通の熱力学では導かれることだと思います．統計力学的にも導かれるものだと思っています．

takeo さんのレス (2007/03/07(Wed) 00:44)

等重率の仮定とは， 系がある一定のエネルギーをもつときの，（ミクロな）状態は全て等しい確率で現れる． だと理解しています． 今考えているのは，平衡状態の統計力学なので，クロメルさんの言うように，非平衡状態で等重率の仮定を持ち出した動的な記述はできないような気がします．

最終的な平衡状態では等重率の仮定により，（桁違いに多い互いに似ている）状態が出現しているということはわかります．

クロメル さんのレス (2007/03/07(Wed) 02:40)

takeoさんの言っている「非平衡状態で等重率の仮定を持ち出した動的な記述はできない」ということは，ふたつの系をくっつけたら，なぜふたつの系は平衡状態に近づいていくか説明できないということですか？それは確かに議論できないと思います．

かず さんのレス (2007/03/07(Wed) 12:07)

＞クロメルさん ＞takeoさん いろいろありがとうございます． エントロピー増大の法則は等重率の原理から導かれるわけですね． ここで確率論的にほぼ妥当なので物理上の「法則」（例外が存在するから）であって数学上の「定理」（例外がない）ではないといっていいでしょうか． あと クロメルさんの ＞状態を表すパラメータがどの値をとる時，最大の確率をとるかを考え，その最大の確率をとるパラメータを持つ状態が実現する という部分なんですが，これがエントロピー増大の法則と自由エネルギー最小の原理（定理？or法則？）につながるわけですね．

最後に takeoさんの ＞エントロピー増大の法則＝ミクロ正準集団という認識 なんですが自分はそのように思っているというか 自由エネルギー最小の原理＝正準集団 の対応関係だと位置付けています． それで一般次元場合のイジング模型（近似解）なんですがエントロピー増大の法則 を用いる場合 エントロピー（Ｓ）の磁化（ｍ）についての微分が０になるという条件式でよろしいでしょうか．

クロメル さんのレス (2007/03/07(Wed) 15:39)

＞かずさん

なるほど，法則の方が適当な言葉のようですね．

＞これがエントロピー増大の法則と自由エネルギー最小の原理（定理？or法則？）につながるわけですね．

その通りだと思います．二つが等価（お互いにお互いを導ける）かどうかはわかりませんでした．熱力学なら，エントロピー増大則から自由エネルギー最小原理を導いてましたけどね．

takeo さんのレス (2007/03/07(Wed) 16:19)

＞クロメルさん そうです．二つの系をくっつけたとき，どのようにして平衡状態に向かう機構を，クロメルさんは等重率の原理をつかって説明なさったからです．（実は私も少し考えました．でも，本当にいいのかなぁと思ったので．）

自由エネルギーの最小性を導く方法は，正準集団で摂動を加えたときを考える方法しか知りません．エネルギー一定のもとでは，自由エネルギーの最小はエントロピー最大を意味するから，，と考えられるなぁとしか理解していませんでした． ミクロ正準集団でエントロピーの変分原理を考える方法があれば知りたいです．

＞かずさん なるほど．正準集団でランダウ疑似自由エネルギーを考えるのと同じように，ミクロ正準集団でも，疑似エントロピーを考えてその最大性から磁化を決めようというのですね． 正準集団では温度一定の環境で自由エネルギーを考えることに意味があります．イジング模型で，何らかの近似をしてエネルギー とエントロピー， が磁化の関数として計算できれば，

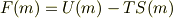
となります．なるべくエネルギーをを小さくして，エントロピーを大きくするような状態が現れます．外からコントロールできるのは 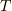のみです． ミクロ正準集団の場合，エネルギー一定の状態を考えなければいけません．エントロピーを磁化の関数で書いても，イジングスピンのように相互作用を持つようなものを考えるときは磁化がエネルギーと直結していて難しいのではないかと思います．

クロメル さんのレス (2007/03/07(Wed) 17:36)

takeoさんに確認して欲しいことがあります．

私の持っている本には「ミクロ正準集団というのは，系のエネルギーを指定した時に得られる状態の分布」書いてあります．同様に，正準分布というのは，「系の温度を指定した時に得られる状態の分布」とあるんですが，これはtakeoさんの知識と一致しますか？基本的なこと概念をよく分かっていなくて，すいません．

takeo さんのレス (2007/03/07(Wed) 19:46)

＞「ミクロ正準集団というのは，系のエネルギーを指定した時に得られる状態の分布」 ＞「正準分布というのは，系の温度を指定した時に得られる状態の分布」

は，私の知識と一致します．

かず さんのレス (2007/03/07(Wed) 20:18)

クロメルさん， takeoさん，またまたありがとうございます．

takeoさんの

＞正準集団でランダウ疑似自由エネルギーを考えるのと同じように，ミクロ正準集団でも，疑似エントロピーを考えてその最大性から磁化を決めよう

の部分なんですがちょうど疑問に思っていたところです． 具体的には長岡先生の岩波基礎物理シリーズの「統計力学」のイジング模型の磁化の温度依存を求める過程なんですが，あの部分でエントロピーが

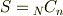
Nは全粒子数，nは上向きのスピンの数 となっていて結果的にエントロピーが磁化ｍの関数で書けるようにもっていっていますよね． だけど，よくよく考えてみるとエントロピーというのは小正準集団で考えるとエネルギーを指定しているのでエネルギーの関数ではじめなければならないはずだと．． 数式で書くと

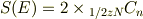
1/2zNは相互作用の総数（というかなんといってよいか）で，nは相互作用が

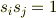
であるようなものの数です．（なんかわかりずらくなってしまいましたがすいません．）

これは「ランダウ疑似自由エネルギー」とか「疑似エントロピー」の話となんか関係があるのでしょうか．

たびたびの質問ですがお願いします．

takeo さんのレス (2007/03/08(Thu) 00:43)

かずさんの話を聞いて悩んでしまいました．考えた範囲で書きます．

長岡先生の教科書が手元にあるので，その部分を読んでみました．問題のところは８章p.232ですね．温度一定の環境で，エネルギーとエントロピーを計算して，自由エネルギーを求めるところです．ここで「エネルギーの見積もりは正しくない」と書かれている一方で「エントロピーは厳密に計算できる」とあります．後者は正しくないのではないかと思いました．スピン相互作用がない状態ない（つまり，好き勝手な方向を向く）を仮定した上でエントロピーを求めているように思えます． 大きく見積もったエントロピーを考えているのではないでしょうか．これも含めてBragg-Williams近似かと． （かずさんの 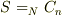は 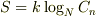の間違いですよね．）

かずさんの言う「相互作用の総数」とは普通「ボンド」と呼ばれるものです．２章の演習問題8で一応は解けていると思ったのですが，これでは磁化が求まりませんね…．

＞これは「ランダウ疑似自由エネルギー」とか「疑似エントロピー」の話となんか関係があるのでしょうか．

Bragg-Williams近似で求められる自由エネルギーは，熱力学的ではありません（凸性がない）．これを「疑似」と言ったわけです．これで相転移現象が説明できます．半現象論的な理論だと思ってよいと思います．

エントロピーをうまく計算して「疑似エントロピー」（この用語は一般に使われてはいません，勝手に私が使っています）が求まれば，相転移が説明できるかなと思いました．

かず さんのレス (2007/03/08(Thu) 13:19)

takeoさん，レスありがとうございます！いろいろと議論できてうれしいです．

なるほどエントロピーも含めてBragg-Williams近似と考えるのが妥当ですね．

＞イジング模型で，何らかの近似をしてエネルギーUとエントロピー，Sが磁化の関数として計算できれば，

とありましたがそのようにエントロピーも近似したということですね． 二次元イジング模型についてはオンサーガーが厳密解を求めているようですが（どう求めたのか知りませんが）そこではたぶん真のエントロピーを求めていると思います．

ちなみに２章の演習問題8ですがこれはボンドを考えているので真のエントロピー（つまりエネルギーの関数の）が求まっておそらく厳密解（一次元の）になっているかと思います．（分配関数から求めたときと答えが同じ）

takeo さんのレス (2007/03/08(Thu) 16:34)

かずさん，どうも．こちらも楽しく議論させてもらっています．

Bragg-Williams近似についてはそれでいいと思います． （個人的な意見ですが，平均場近似は平均磁化からの揺らぎが小さいとして導出する方が議論がすっきりしていて好きです．）

＞二次元イジング模型についてはオンサーガーが厳密解を求めているようですが（どう求めたのか知りませんが）そこではたぶん真のエントロピーを求めていると思います．

二次元イジング模型の厳密解（分配関数）を求める方法はいくつかあるみたいですが，本当にエントロピー（状態数）を求められるのでしょうか．一般に状態数を求めるのは簡単な系でも容易ではないです．また一般に分配関数を求めるのは比較的容易ですよね． 最近接相互作用のみの二次元イジング模型で磁場がない場合は厳密解が存在します．しかし，これを求めるのも決して容易ではないことを考えると…．

＞ちなみに２章の演習問題8ですがこれはボンドを考えているので真のエントロピー（つまりエネルギーの関数の）が求まっておそらく厳密解（一次元の）になっているかと思います．（分配関数から求めたときと答えが同じ）

そうですね，これは厳密解です．うっかり勘違いしていて，どうして相転移しないのか悩んでいました．一次元イジングは相転移しませんね．平均場近似を用いると一次元系でも相転移してしまうのでした．

かず さんのレス (2007/03/08(Thu) 19:09)

takeoさん，今回のスレの目的は大体達成されたように思います．感謝しています．

そこでちょっと考えたんですけどもう少し深く統計力学関連の分野について議論というか質問というかしたいんですけどどうでしょうか．内容としては当たり前のように思う問題とかテーマについてちょっとした疑問を議論していくような感じ（たとえば，長岡先生の統計力学の本とか久保先生の演習書を題材にして概念的なこと，複雑な計算には立ち入らずに）ですけど，ここでひとまず終えたいと思っているなら全然かまいません．

takeo さんのレス (2007/03/08(Thu) 22:26)

概念的なこと，原理的なことは，私も好きです．よろこんで議論したいと思います． では，新しいスレッドで始めましょうか．

かず さんのレス (2007/03/09(Fri) 11:59)

ありがとうございます． では気長にあせらずじっくりと続けたいと思います．