けん（大学1年） さんの書込 (2007/03/04(Sun) 21:36)

慣性系（O系）に対して原点を共有し，角速度ベクトルωで回転運動する座標系（O'系）を考える．

このとき，O系でみたωの時間微分dω/dtと，O'系でみたωの時間微分（d'ω/dt とします）は等しいそうです．ですが，感覚的な理解ができません．O'系は，ベクトルωの周りを回転するわけですから，O'系でωをみると，変化しないような気がしてしまうのです…．

よろしくお願いします．

zoro さんのレス (2007/03/04(Sun) 22:12)

けんさん，

このところ細かい点に文句を付けているようで気が引けますが，老人の戯言として気楽に見てください．

☆問題が明確でない！☆本来の問題は，

「（O系）に対して原点を共有し，角速度ベクトルωで回転運動する座標系（O'系）を考える． このとき，O系でみたωの時間微分dω/dtと，O'系でみたωの時間微分（d'ω/dt とします）は等しいそうです．」

だけなのでしょうか？私にはそう思い難いです．

☆出典を明記した方がいい！☆私見ですが...，反論もあると思います．

多くの人々が見ている事も考えると，もし問題が書籍から取られているならば，明記して論議する方が良いと思います．

また，質問する上で，簡潔にされているのだと思いますが，重要点を欠落していると，回答者が戸惑う事も在るでしょう．

☆面白い質問の可能性がある☆とも思います．

それ故に，質問も丁寧にして，疑問点を明快にしてガッチリ論議されると良いですねえ．

けん（大学1年） さんのレス (2007/03/05(Mon) 00:29)

問題が明確でないようですみません．

まず，状況設定についてですが，

慣性系（O系）に対して原点を共有し，角速度ベクトルωで回転運動する座標系（O'系）を考える．

のみです．

任意のベクトルAの時間変化を考える． 長い議論の後，

O 系でみたAの時間微分d A/dt O'系でみたAの時間微分d'A/dt に対し， dA/dt=d'A/dt+ω×A が導かれています． 特にAにωを代入したとき， O系でみたωの時間微分dω/dtと，O'系でみたωの時間微分（d'ω/dt とします）は等しい という結果が導かれています．最後の部分が，感覚的に理解できないというのが質問です．よろしくお願いします．

なんとなく さんのレス (2007/03/05(Mon) 00:39)

こんにちは，なんとなくです．

zoroさんの書かれたことはもっともなのですが，文面からおそらく物理では基本的な良く出る問題で，一般論の話ではないかと思います．そうなら，直観的な理解に戸惑っているのでしょう． 私は問題は明確だと思いますので，以下の考えを参考にしてください． 一般に回転座標系から静止座標系への座標変換に対して，質問の記法で，ベクトルＡの変化（時間微分）は， dＡ/dt=d'Ａ/dt+ω×Ａ・・・? と表せます．?でＡ自身をωととれば，直ちにdω/dt=d'ω/dtが成り立つことは明らかです． これを直観的に考えるには，回転座標系と共に回転している観測者を想像します．この観測者は回転座標系の上ではなく，その周りを同じ角速度ωで回転しているものだと思ってください．観測者にとって，（観測する）角速度が0からΔωに変化したとき，観測者は付いてゆかず，その変化を観測でき，角速度が０からΔωになる，つまり微分d'ω/dtを観測します．一方静止座標系の観測者はωからω＋Δωになること（dω/dt)を観測します．どちらも同じ値になることは明白です． 一般のベクトルＡは回転座標変換における基底ベクトルの変換による?の第二項を変化分として残しますが，回転ベクトルωそのものは，原点で回転平面に垂直なため，この変化分が０になる（一種の）特異点であるわけです．?の導出過程と，上記の観測者の意味を突き合わせて考えてみてはどうでしょう．

けん（大学1年） さんのレス (2007/03/05(Mon) 00:51)

なんとなくさん，レスありがとうございます．

回転座標系での観測者は，（観測する）角速度が0からΔωに変化したとき，付いてゆかず，その変化を観測でき，角速度が０からΔωになる，つまり微分d'ω/dtを観測する，とするとうまくいくんですね． ωが変化するとき，回転座標系での観測者もωの変化に合わせて移動させていました．

よく分かりました．ありがとうございました．

zoro さんのレス (2007/03/05(Mon) 06:03)

けんさん，

私は，学生の頃，この問題の真意が判らずに苦労しました．回転系の座標，例えば，地球の自転によるコリオリ成分と，円運動する場合の遠心力と一体何が違うか，人知れずに悩みました．

数式上では当たり前でも，その本質を納得できれば良いですね．

けん（大学1年） さんのレス (2007/03/05(Mon) 15:49)

＞なんとなくさん

＞観測者にとって，（観測する）角速度が0からΔωに変化したとき，観測者は付いてゆかず，その変化を観測でき，角速度が０からΔωになる，つまり微分d'ω/dtを観測します．

観測者にとっては，O系が角速度-ωで回転するように見えると思うのですが…．

＞zoroさん

僕は直感的な理解ができなくて困っていることがよくあります．数式上では当たり前なのですが…．

zoro さんのレス (2007/03/05(Mon) 17:15)

けんさん：

>僕は直感的な理解ができなくて困っていることがよくあります．数式上では当たり前なのですが…．

逆に言えば，この瞬間に物理の醍醐味に一歩近づけたのだと思います．

お書きになった式で，dA/dtは，あるベクトル量Aを，ある慣性系から見た時の時間変化ですね，太陽から地球の台風を観察している感じでしょうか．その同じ量を地球上の我々が見た変化を見ようとすると，（A'＝ A）でも （dA'/dt ≠ dA/dt）となる訳ですね．

太陽から台風を記述するときには，dA/dtだけで，しかも基底ヴェクタは固定されているので，時間依存性はありません．しかし地球は自転運動(ω)をしていて，地表のわれわれが決める基底ベクトルはいやでもωにより剛体として回転しまうわけですね．

この手の考え方を理解すれば，地球規模でも，どこかの銀河星団のダイナミックスでも，原子核の運動でも皆同じなのは，物理学の良い所でしょうかね．

もとに戻れば，A = ωでは，自分が自分を捩じれない，もしくは自分が自分に回転トルクを掛けられない；(ω x A = 0)，と思うだけではいけませんか？

けん（大学1年） さんのレス (2007/03/06(Tue) 00:31)

太陽から台風を見ることを考えるっていうのは思いつきませんでした．ω一定でAが変化する場合はイメージをつかめました．ありがとうございます．

A=ωの場合，ω自身が変化してしまうので，O'系から見たωの時間変化がイメージできなくて困ってます．

zoro さんのレス (2007/03/06(Tue) 00:54)

久々に徹夜作業をしたので簡単にコメントします．

我々は，スケールも小さく・運動速度が小さいので，コリオリの力を直接には体験できませんが，天上を見上げる事で，地軸の回転を察知できます．この回転は月との距離が離れるにつれてユックリになるとはいえ，まだ十分に一日は24hrをたもっています．

＃TVのうろ覚えですが，昔の戦艦が練習している時は，命中精度が高いのに，戦場にでると駄目になる．コリオリの力の為せるものと聴いた気がします．軍隊が計算機に興味を持ったのも，砲弾のシミュレーションと聞いた様な気がします．

>A=ωの場合，ω自身が変化してしまうので，O'系から見たωの時間変化がイメージできなくて困ってます．

この部分は，別の問題ですよね，そうではなくないでしょ？この点は重要だと感じるので，もし具体例なども含めて，詳しく疑問を出されると，素晴らしい解説を戴ける予感がします．

けん（大学1年） さんのレス (2007/03/06(Tue) 01:04)

これはNo.14728での疑問です． ω自身が変化する例としては， 遊園地にある，回転軸が時間変化しながら回転軸の周りを客が回っているもの などがあると思います．

zoro さんのレス (2007/03/06(Tue) 01:53)

そういう意味では，メリーゴーランドの外で見ているお母さんがωを調べる為にVTR撮影し・ωの時間変化をプロットしたのと，メリーゴーランドに乗ったお子さんが景色を撮影したVTRからω'の時間変化をプロットしたのとを比較すれば全く同じ結果となると思います．

それと全く並行的に，地球を太陽から眺めたωと，地球から北極星を眺めたω'とに違いがあるのでしょうかね？

ちょっと気になるのは，d'A/dt みたいな記法は一般的ですか？私は手元に，流体力学と電磁気の本しか在りません．うろ覚えですが，記法は，イメージと密接なので明日にでも調べてみますが．

けん（大学1年） さんのレス (2007/03/06(Tue) 23:30)

メリーゴーランドの場合，ωの向きは変わらず，大きさのみが変化します．向きも時間変化するような例でイメージがわきません．

それから，先ほど出てきた台風についてです．お書きになったこととは問題点は違うことですけれど． 台風は，太陽から見た場合，放射状に吹き込み，台風の目自体は移動しないかと考えました．もしそうだとすると，半時計周りに自転している地球から観測すると，北半球では，台風が東から来ることになります．しかし，これは，天気は左からやってくるという，よく知られた事実と矛盾してしまいます．間違っているのはどの部分なのでしょうか？

d'A/dt という記法ですが，大学の講義で使われている教科書には，載っています．

zoro さんのレス (2007/03/07(Wed) 02:32)

>メリーゴーランドの場合，ωの向きは変わらず，大きさのみが変化します．向きも時間変化するような例でイメージがわきません．

すると，いったい何を想定して悩んでいるのか判りません．この点に付いては，もう少し質問を明確にしてください．コマの問題などは，それに近いでしょうが，軸先に摩擦力が入るので解析は困難だと思います．もしこの手の分野の論議がしたいなら，私は論議する能力がないので降ります．

台風の目の運動は，地球大気の大規模な大気・海流・太陽の活動等の結果に支配されるので，簡単なモデルでは算出が出来ないでしょう．将来，地球シミュレーション計画にでも参加されるのも良いかも知れません．

台風を例にとったのは，中心に向けて吹き込む風が，圧力勾配だけで決まらずにコリオリの力によるという点を言いたかっただけです．むしろ大砲のケースの方がよかったかも知れませんね．

私は，天候現象(地球物理)を良く知らないのですが，天候の変化が西から東に動くのは，偏西風の存在が主要な要因だと思っていました．しかし，偏西風の出来る構造にや，蛇行などにはコリオリの力が関与するのだろうと推測しています．

>d'A/dt という記法ですが，大学の講義で使われている教科書には，載っています．

もし宜しければ，その教科書をお教え下さい．共通認識を明確にしたいと思います．

ひょっとすると，その本の記法の為に，大きな誤解をされているようにも思います．回転系の話は，初等力学や初等ベクトル解析などで，頻繁に取り上げられているテーマだと思うので，生協や図書館で他の本をご覧になっては如何ですか．

けん（大学1年） さんのレス (2007/03/07(Wed) 18:14)

遊園地にある，回転軸が時間変化しながら回転軸の周りを客が回っているものという例があります． メリーゴーランドの回転軸を向きも時間変化させるのと本質的には同じです．ただし，乗り物が地面にぶつかったりすることはありませんが．

教科書ですが， 理工学の基礎力学培風館です．

zoro さんのレス (2007/03/07(Wed) 19:30)

>遊園地にある，回転軸が時間変化しながら回転軸の周りを客が回っているものという例があります．

ここまで複雑な問題を解けなければいけないとは思えませんが...，なにか具体的に解くべき課題があれば別ですが，その場合，もはや物理の問題から離れてしまうように思います．

むしろ，地球での問題をしっかり解けば，原理的にはどんな問題も手間隙の違いだとおもいます．

>理工学の基礎力学培風館

ISBN4-563-02268-3のようですね．近くの区と都まで検索しましたが無いようです．培風館のサイト情報の目次から拝見すると標準的な教科書のようですね．

すると，問題は，式の何処の部分が理解できないかを突き詰めて示されないと，こちらも説明のしようがありません．この掲示場板では，数式は使えますが，図が使えないので，私の能力では表現のしようが無さそうです．

むしろ，判り易そうな力学の本を図書館から借りてきて，上記の教科書と付き合わせると良いと思います．

私の推測では，お使いの教科書は，慣性系のヴェクタ表現と回転系のヴェクタ表現との区別が明確でない為に，簡単な話が難しくなっているように感じます．

巧く説明できなくて御免なさい．

Joh さんのレス (2007/03/07(Wed) 21:34)

けんさん＞

回転系における見かけの力の話だと思うのですが，地球の自転では，回転速度がほぼ一定ですので，遠心力とコリオリ力だけが考慮されると思います．地球を例にとった問題では，私がいままでみたことのある教科書では全て，自転速度はほぼ一定と扱われていました．

しかし，例えばヘリコプターの回転翼の動力学を考える場合，スロットルの変化に応じて回転数が変わり，回転速度の変化によって生じる見掛けの力が生じます．この力は地球モデルには出てきませんが，非常に大事です．

問題に応じて，適切な仮定を置くことが大事なのであって，地球のモデルだけ考えればよいというzoroさんの意見に惑わされないで下さい．自分が興味を持ったモデルを，しっかりイメージが湧くまでじっくり勉強なさって下さい．

けん（大学1年） さんのレス (2007/03/07(Wed) 23:14)

＞zoroさん

レスありがとうございます． ＞ここまで複雑な問題を解けなければいけないとは思えませんが...，

今の僕には難しすぎるので，解くことは考えていません．ただ，dω/dtと，O'系でみたωの時間微分（d'ω/dt ）とが等しくなることのイメージを，ωが向きも含めて時間変化する例で，ほしいだけなのです．厳密な理解でなく，感覚的な理解を求めています．

＞私の推測では，お使いの教科書は，慣性系のヴェクタ表現と回転系のヴェクタ表現との区別が明確でない為に，簡単な話が難しくなっているように感じます．

教科書では，回転系でのベクトルは全て'をつけて表現されています．

＞Johさん

レスありがとうございます． ＞ヘリコプターの回転翼の動力学を考える場合，スロットルの変化に応じて回転数が変わり，回転速度の変化によって生じる見掛けの力が生じます．

回転の角速度をωとしたとき，慣性系（O系）に対して原点を共有し，角速度ベクトルωで回転運動する座標系（O'系）を考えます．dω/dtと，O'系でみたωの時間微分（d'ω/dt ）とが等しくなることのイメージがほしいのですが，どうしてもイメージできません．よろしければ解説をお願いします．

Joh さんのレス (2007/03/08(Thu) 01:12)

私には，「dω/dtと，O'系でみたωの時間微分（d'ω/dt ）とが等しくなることのイメージ」というのは持てません．何をもって，イメージと呼んでいるのでしょうか？イメージという意味がよく分かりません．

どこの座標系でも，その座標系にいる人というのは，自分が動いているとは思っていません．静止座標系から見れば，本当は動いているわけですが，「自分は動いていない」と信じる代わりに，見かけの力を感じるわけです．d/dt = d/dt' + ω×より，dω/dt = dω/dt'になりますが，その直観的イメージは，「Ｏから見れば，Ｏ’がぐるぐる回っている」「Ｏ’から見れば，Ｏ’がぐるぐる回っている」という感じでよくはないですか？公園で，グルグル回る遊具に乗ってずっと回ってると，自分じゃなくて世界の方が回っているように感じてきます．そんな感じだと思います．

けん（大学1年） さんのレス (2007/03/08(Thu) 17:06)

イメージというのは，静止系でωの変化を目で見たときと，回転系でωの変化を目で見たときに，その時間変化が等しくなることをイメージできるようになりたいということです．ここで「見る」というのは，数式による表現でなく，ベクトルの変化の視覚的理解を指して使っています．

ミュフ猫 さんのレス (2007/03/08(Thu) 18:00)

横レス失礼します．

>静止系でωの変化を目で見たときと，回転系でωの変化を目で見たときに， >その時間変化が等しくなることをイメージできるようになりたいということです．

こういう考えではダメでしょうか？ 非相対性力学の立場で，例えば，地上の静止系から見たときの， 打ち上げロケットの加速度と，等速で上昇するエレベーターに 乗る人の観測系（エレ系）から見たそれとは，同じですよね？ 当然，同時刻での位置や速度は，二つの観測系で異なりますが， 加速度（速度変化率）は同じはず． この考え方を，そっくりそのまま，回転座標系に当てはめて よいのではないでしょうか？つまり， 「同時刻における偏角（位置）や角速度（速度）は， 二つの観測系で異なるが，角加速度（速度変化率）は同じに 見えるはずである．」 というように． でも，コリオリ力とか絡むから，そんなに単純じゃないかも・・・．

けん（大学1年） さんのレス (2007/03/08(Thu) 18:08)

＞ミュフ猫さん

言われてみればそうですね．なんとなくイメージが少しできました．ありがとうございます．

yama さんのレス (2007/03/13(Tue) 23:38)

いろいろな議論が展開されたようですが，初めの質問にはまだきちんとした回答がされていないように思います．そこで私なりに考えたことを書いてみます．

まず「O'系でみたωの時間微分」についてですが，このωはあくまでもO系に対するO'系の回転の角速度であって，O'系から見たO'系の角速度ではありません．（もしそうだったら ω=0 になってしまいます．） つまり，O系に対するO'系の運動をO'系の立場で表すということですから，これを感覚的に理解するというのはかなり無理があるように思います． しかし，O'系の座標軸を運動する物体の慣性主軸に一致するように設定するとO'系での運動方程式がかなり簡単な形になります．これがオイラーの運動方程式です．従ってオイラーの運動方程式の意味をきちんと理解するためには，「O'系でみたωの時間微分」というものをを正しく理解することが必要だと思います．

O'系でみたωの時間微分をd'ω/dtで表すのは，ωがO系に対する角速度であることをはっきりと示すためだと思います．ランダウ=リフシッツ「力学」でもこのような表し方がされています．dω'/dt のように表してある本もありますが，ω'がO'系から見たO'系の角速度であると誤解されるおそれがあるように思われます．

dω/dt=d'ω/dt を感覚的にどのように理解するかですが，ωの大きさだけが変化する場合はO系でもO'系でも同じように変化することはわかると思います． ωの向きが変化する場合は，感覚的には分かりにくいかもしれませんが，これは回転軸の向きが変化するということです． O系で回転軸の向きが変わる場合は，O'系においてもこの回転軸の向きが変化します．たとえば，ある瞬間にz'軸を中心に回転していたものが，次の瞬間にはz'軸から少しずれた軸を中心に回転するようになるというように・・・． dω/dt=d'ω/dt ということは，この回転軸の変化する向きと変化の速さが，O系でもO'系でも同じになるということです．

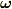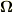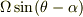例として地球の回転を考えてみます． 地球は約24時間の周期で自転しながら，同時に自転軸が公転軸（公転軌道面の法線）に対してθ=23.4°の傾きを保ちながら公転軸のまわりを約26000年の周期で回転（歳差運動）しています． 地球全体としての回転の角速度は，自転の角速度 と歳差運動の角速度 を合成したものになるので，その回転軸はほんのわずかですが自転軸からずれています．このずれの角度を α とします． 回転軸は公転軸に対して角度 θ-α を保ちながら 回転するので，回転軸の向きの変化の角速度は です． 一方，地球の自転にともなって，回転軸は自転軸に対して角度αを保ちながら自転軸のまわりを１日で１周します．このとき，回転軸の向きの変化の角速度は 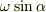です．つまり地球に固定した座標系では，この角速度で回転軸の向きが変わっているわけです． ところがベクトル 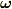と 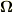の合成の図を描いてみればわかるように 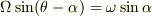の関係があります． 従って，回転軸は慣性系から見ても地球に固定した座標系から見ても同じ角速度で向きを変えることになります．角速度の大きさだけでなく，変化する向きも同じになることは図を描いてみれば分かります．

toorisugari no Hiro さんのレス (2007/03/15(Thu) 12:55)

yamaさん，すばらしい記事ありがとうございます．

# こういう記事，FAQか何かで残したいですね．

けん（大学1年） さんのレス (2007/03/15(Thu) 22:43)

＞yamaさん

＞たとえば，ある瞬間にz'軸を中心に回転していたものが，次の瞬間にはz'軸から 少しずれた軸を中心に回転するようになるというように・・・．

z'軸は，O'系の回転軸として定義されているのですか？z'軸が回転軸からずれることが理解できません．

それから，地球の回転についてですが， 回転軸の向きの変化の角速度 とは何なのか教えて下さい．

他の部分は理解できたと思います．ありがとうございます．

ｙama さんのレス (2007/03/16(Fri) 09:35)

>z'軸は，O'系の回転軸として定義されているのですか？z'軸が回転軸からずれることが理解できません．

これは一つの例としてそのような場合もあるということです． たとえば，O'系がコマに固定された座標系で，コマの軸がz'軸であるとします． z'軸は初めはO系（慣性系）のz軸と一致していて，コマはz'軸のまわりに回転しているとします．O系ではz軸のまわりに回転しているわけです． この状態から，コマに外力を加えて軸の向きをゆっくりと90°変えるとします．すなわちO系のx軸のまわりにコマ全体を90°回転させます．この回転の結果，コマの軸（z'軸）はO系のy軸に一致するようになります． この過程では，コマの回転軸がz'軸のまま，回転軸が90°向きを変えたように思われるかも知れませんが，実はそうではありません． というのは，回転軸の向きを変えるときにx軸のまわりに回転させるので，そのときコマはx軸方向の角速度も持つことになります．そうするとコマ全体の角速度はz'軸方向の角速度とx軸方向の角速度を合成したものになり，その結果，コマ全体の角速度の向きはz'軸からずれることになります．これはコマの回転軸がz'軸からずれるということです． 回転軸はz'軸からx軸の向きに少しずれることになりますが，O系のx軸は，O'系から見るとz'軸のまわりに回転しているので，コマ全体の回転軸はz'軸のまわりを回転することになります．

回転軸の向きの変化の角速度というのは dφ/dt のことです．ただしdφは時間dtの間に回転軸の向きが変化した角度です．

けん（大学1年） さんのレス (2007/03/19(Mon) 13:47)

回転軸とコマの軸が一致しないわけですね． 丁寧な解説，ありがとうございました．

クロメル さんのレス (2007/04/10(Tue) 01:19)

すいません．少し乗り遅れてしまいましたが，yamaさん，質問していいですか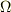？ は，公転面に垂直なときしかサインの式の等号が成り立たないように思うのですがいかがでしょうか？

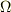自分の書いた図が正しいか心配です． イメージとしては の大きなベクトルの先端から，ぴょこっと任意の方向に が出ているのかと思うのですが，あってますか？

ｙama さんのレス (2007/04/10(Tue) 14:02)

その通りです．歳差運動の回転軸が公転面に垂直だから等号が成り立っているわけです．

>イメージとしては 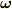の大きなベクトルの先端から，ぴょこっと任意の方向に 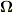が出ているのかと思うのですが，あってますか？

任意の方向ではなくて，公転面に垂直な方向に 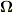が出ているわけです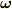． が 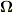のまわりを回転するわけなので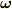， と 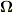の始点をそろえたほうがイメージとして分かりやすいかもしれません．

クロメル さんのレス (2007/04/11(Wed) 20:24)

yamaさん，回答ありがとうございます．

なるほど，歳差運動は公転面に垂直な回転なのですね． 僕は章動という運動と混同していたようです． ありがとうございました．