あさ（大学２年） さんの書込 (2007/03/03(Sat) 12:30)

こんにちは．お久しぶりです． 最近統計力学みたいな？熱力学を勉強していて，ふと思った疑問があるので教えてください．

閉じた系が大きな熱浴と接している状況を考える．閉じた系は熱浴と同じ温度． 閉じた系と熱浴が熱平衡の時閉じた系のF（ヘルムホルツエネルギー）は最小， ということは，つまり閉じた系と熱浴の温度が等しくかつ閉じた系では粒子がとり得るエネルギーの分布が小さくなるor高いエネルギーの分布が少なくなる（但し平均（＝温度）は同じ）ということを意味していますか？分配関数が大きくなるということは，分配関数（状態和）の項数が減るか，あるいはボルツマン因子のeの指数部分に出てくるエネルギーεの値が小さいものが多くなるということを意味しているのですよね？だからエネルギー分布は，温度（平均）は同じでも，エネルギーの高い部分が減る状態に（熱平衡時には）近づいていくということなんですよね？

どなたか解答よろしくお願いいたしますm(__)m

takeo さんのレス (2007/03/04(Sun) 23:13)

おもしろそうだなぁと思って見ていたのですが，残念ながらあまり意味がわかりません．すごく興味があるので，もう少し詳しく書いてほしいです．

前半でおっしゃっているFが最小というのは， まず等温で平衡状態の系があって，その系に少しだけ変化を加えるたとき，自由エネルギーを最小にする状態（新たな平衡状態）になること． だと私は理解しています．純粋に熱力学の議論です．

このハミルトニアンの変化で，ボルツマン因子（つまりはエネルギー分布）も変化しています．そのことと自由エネルギーの最小性とを結びつけるのは，そんなに単純なものではないと思います．統計力学的にはファインマンの不等式に行き着くのではないでしょうか．

かず さんのレス (2007/03/06(Tue) 20:28)

はじめて投稿します．物理学科所属予定の学部一年のものです． 自由エネルギーが最小＝自由エネルギーの統計力学的表式から分配関数が最大 ＝ 「分配関数（状態和）の項数が減るか，あるいはボルツマン因子のeの指数部分に出てくるエネルギーεの値が小さいものが多くなる」 という部分につきましてはまず前者は誤りです．各項（eの部分）は常に正値をとるから．後者は要するに個々のエネルギー固有地が最小に？なるように実現されるという意味でおそらくただしいと思うのですが．．． あとひとつ気になる箇所が「平均（＝温度）」ですが温度が系のエネルギー分布の平均を表しているということでしょうか．

takeo さんのレス (2007/03/06(Tue) 23:23)

かずさん，はじめまして．

＞自由エネルギーが最小＝自由エネルギーの統計力学的表式から分配関数が最大

は正しいですか？ 熱力学的には自由エネルギー最小の状態が実現されます．しかし，統計力学的には系を決めた時点（ハミルトニアンと温度を決めた時点）で分配関数 は決まります．ですから分配関数から求めた自由エネルギーは既に平衡状態を表す最小なものだと思うのです．

とすると

＞後者は要するに個々のエネルギー固有地が最小に？なるように実現されるという意味でおそらくただしいと思うのですが．．．

に関してですが，ボルツマン因子 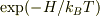も完全に決まっている，つまり固有値も定まっていると思います．