toorisugari no Hiro さんの書込 (2007/02/23(Fri) 21:31)

別スレッドで議論していた，磁気双極子，及び，電磁石のローレンツ変換の話は今後こちらに移動させていただきます．

電磁気学，及びそれにかかわる諸現象の物理的・数学的構造に関わることなら，なんでも結構です．

とりあえず，

これまでの議論で感じた事を書いておきます．

電磁気学は本質的に相対論的なんですね．(式がローレンツ共変なのは知っていますが．)

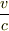の一次で現れる項は非相対論的な説明で理解できると思っていたのですが，運動する電磁石の電気双極子化は非相対論的な議論では導出できないと言うのは勉強になりました．

そこで，疑問に思うのですが，ほかの 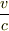の一次で現れる(速度に比例する)現象もすべて非相対論的には理解できないのでしょうか?

電流は電荷と速度から非相対論的に説明されていますよね． これは，正しいのでしょうか．

特に電流密度とはなんだろうか?「正電荷が静止していて負電荷が移動している」様子は具体例であって，定義ではないのではないか? 粒子に依存しない考え方をすべきではないか?

などと妄想しています．

とりとめないことを書いていますが，何か教えていただければ幸いです．

MXK さんのレス (2007/02/23(Fri) 23:03)

toorisugari no Hiro さん 新しいスレッド開設ありがとうございます．

ローレンツ変換は

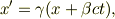
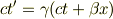
ただし，

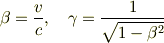
ガリレイ変換

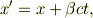
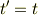
は，単に 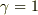の場合ではない． むしろ，1次ローレンツ変換

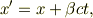
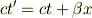
になる．

（非相対論的）電磁気では，この変換がポイントになると考えます．

yama さんのレス (2007/02/23(Fri) 23:10)

相対論以前の電磁気学は当然非相対論的に理解されていたわけで，それによって説明された現象も多いと思います．

例えば光のドップラー効果があります．非相対論的に考えると光源が動く場合と観測者が動く場合で違った式になりますが，級数展開して v/c の２次以上を無視すれば一致しますし，相対論的な式でv/c の２次以上を無視したものとも一致します． また光行差も v/c の一次の項までなら非相対論的に説明できますね．

yama さんのレス (2007/02/24(Sat) 09:22)

直線電流で電場が生じる現象は，v/c については一次ですが，電荷の速度Vについても V/c の一次の式であり，これら一次の項が積の形で関係するので，速度の二次の項が関係すると考えるべきでしょう． vとVが同程度の大きさであれば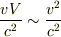， と考えることができると思います．

yama さんのレス (2007/02/24(Sat) 13:58)

電流密度とは，電荷流束密度すなわち電荷の流れの密度だと思います． 従って，その大きさは，電荷の速度に垂直な単位面積を単位時間に通過する電荷量を表すことになります． 流体力学では質量流束密度を考えますが，質量を電荷に置き換えて考えたものが電流密度に相当すると思います．

toorisugari no Hiro さんのレス (2007/02/24(Sat) 14:49)

MXKさん，yamaさん，ありがとうございます． 新鮮な知識の洪水で，いま目ぱちくり状態です．

たくさんあってどれから考えていけばいいかわからない， 未消化のくせに，また質問させてください．

電荷密度から定義し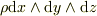た電荷 はローレンツスカラーですよね． 電流密度から定義した電荷 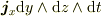はローレンツスカラーなのですかね？違うのなら 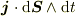はどうでしょう？

yama さんのレス (2007/02/24(Sat) 20:51)

最初のものはスカラーですが，あとの２つは電荷の静止系で0になってしまうのでスカラーではないと思います．

toorisugari no Hiro さんのレス (2007/02/25(Sun) 17:45)

> ガリレイ変換 >

> は，単に 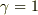の場合ではない． > むしろ，1次ローレンツ変換 >

> になる．

>（非相対論的）電磁気では，この変換がポイントになると考えます．

目から鱗がすごく落ちました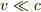． はガリレイ共変の世界だと思っていたのが，大間違いだったのですね．