トンガリ さんの書込 (2007/02/21(Wed) 19:08)

最大半径Ｒ＝0.1[m]の立てたビーカーに比重１の青色水を十分入れ， ビーカーの鉛直軸周りに角速度ω＝9.9[ラジアン／s]で回転させると， 青色水が最大半径で受ける遠心加速度はＲω^2＝9.8[m／s^2]＝1[重力加速度]となり， 青色水の自由曲面の形は，最大半径での傾斜角θ＝45°の放物線を回転した面である．

そこで問題を作りました． 青色水の上に比重γ＝0.8の灯油を静止状態でＨ＝0.5[m]入れて， 同じ角速度で回転させると， 青色水と灯油の境界面の形は，どのような面になるでしょうか．

私は未だ解答を持っていません．

yama さんのレス (2007/02/21(Wed) 23:15)

ビーカーとともに回転する座標系で考えた場合，境界面は遠心力のポテンシャルも含めた等ポテンシャル面，すなわち回転放物面になるでしょう． 油があってもなくても同じだと思います．

トンガリ さんのレス (2007/02/22(Thu) 09:55)

灯油の自由曲面は青色水単体のときと同じ回転方物面であって， 灯油の深さは半径のどこにおいてもＨ＝0.5[m]一定なので，灯油があってもなくても同じでした． つまらぬ問題で申し訳ありませんでした．

toorisugari no Hiro さんのレス (2007/02/22(Thu) 19:10)

トンガリさん

> つまらぬ問題で申し訳ありませんでした．

そんなことはないですよ．(もう一つの問題の方は，，，すいません，つまんないです．)

(静水の)水面が何故水平になるかをきちんと答えられる人はなかなかいないと思います． この問題は，それを理解できる良い問題と思います．

(個人的には，具体的な数値を与えられるより，パラメータと変数を与えてもらった方が問題の見通しが良いと思いますが．)

# 実はすぐにはわからなかった．

山旅人 さんのレス (2007/02/24(Sat) 22:08)

>> yama さん，お久しぶりです．

この問題の解として， > 境界面は遠心力のポテンシャルも含めた等ポテンシャル面，すなわち回転放物面

は，私もその通りだと思うのですが，いわゆる <b>安定な境界面が等ポテンシャル面</b> であることは，どのように示せばいいのかご教示くださいませんか． 何かを最小 （極小） にしているのでしょうが，私はこの 「何か」 がわからないのです．

最も基本的な，一様重力場での水面が平面 （いわゆる <b>水平面</b>） となることも，これで…

yama さんのレス (2007/02/24(Sat) 23:36)

安定な平衡状態では，全体のポテンシャルエネルギーが極小になります．

重力も遠心力も質量に比例するので，単位質量当たりのポテンシャルエネルギーを とすると，密度 の液体の微小体積 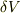のポテンシャルエネルギーは 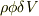となり，これを積分したものが全体のポテンシャルエネルギーです．

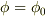の等ポテンシャル面があって，この面より低ポテンシャル側が密度 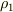の水，高ポテンシャル側が密度 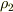の灯油で満たされているとします．当然 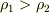です． この状態がポテンシャルエネルギーの極小状態であることを示すには，境界面に微小な変動を与えたときに全体のポテンシャルエネルギーが増加することを示せばよいはずです． 境界面の微小変動の結果，低ポテンシャル側の体積 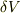の水が灯油に置き換わり，高ポテンシャル側の体積 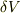の灯油が水に置き換わったとします．その結果，低ポテンシャル側の質量が 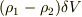だけ減少し，高ポテンシャル側の質量が 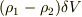だけ増加します． ということは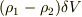， の質量が低ポテンシャル側から高ポテンシャル側に移動したことになるので，全体のポテンシャルエネルギーは増加することになります． このことは微小変動でなくてもなりたつので，この状態はポテンシャルエネルギーの最小状態であり，最も安定な平衡状態であるといえるでしょう．

山旅人 さんのレス (2007/02/25(Sun) 08:47)

そうですよね．私もずっとそのように理解していたつもりだったのですが，δＶ の移動で全体のエネルギーは変化しないのではないかと（急に）思い込んでしまい，迷子になっておりました． ありがとうございました．

toorisugari no Hiro さんのレス (2007/02/25(Sun) 15:19)

> 安定な平衡状態では，全体のポテンシャルエネルギーが極小になります．

付け足し．

全エネルギーは運動エネルギーとポテンシャルエネルギーの和です．振動のように一般には両者の間にやりとりがあります．

静止状態になるためには，運動エネルギーが0(=極小)，そして，運動エネルギーへの移動が起きないようにポテンシャルエネルギーが極小にならなければいけません．(「最小」でも良いのですが，一般的には極小です．)

# 一般的な初期状態から安定な平衡状態を得るためには，微小な散逸効果を考えなければいけません．(そうでないと振動＝波動が無限に続きます．)

yama さんのレス (2007/02/25(Sun) 20:36)

私は静力学的な釣り合いの状態を考えたのですが，その状態に到達する過程においては確かに運動エネルギーや散逸効果を考える必要がありますね．

toorisugari no Hiro さんのレス (2007/02/26(Mon) 18:29)

本当はポテンシャルが極小と言うより，ポテンシャルのグラディエントの2乗積分 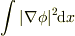が極小の方が正しいのですが，場のラグランジアンの議論+体積保存の議論がよくわかりません．．．．．

yama さんのレス (2007/02/26(Mon) 22:50)

ラグランジアンについては私もよく分かりません 無限自由度だからラグランジアン密度を考えないといけないように思われますが，液体内部では圧力を及ぼし合うだけで，それ以外に複雑な相互作用があるわけではないので，特にラグランジアンを考える意味があるかどうか・・・？ いずれにしても，ラグランジアンからは普通の流体の運動方程式が導かれるだけだと思います． なお，回転する円筒中の液体の表面形状を求める問題は，流体力学の本によると，非圧縮性流体にオイラー方程式を適用して求められるようです．