イオ
イオ
けん(大学1年) さんの書込 (2007/02/21(Wed) 17:54)
木星の衛星イオは平均42.5時間で木星を1周する.地球から見たイオの見かけの公転周期と平均値とのずれが最大になるのはいつか.
「木星と地球を結ぶ直線が地球の公転軌道に接するとき」と答えに書いてありました.
イオの公転周期が静止系から見るのと地球から見るので変わることさえ理解できません.イメージがつかめないのです. よろしくお願いします.
Re: イオ
toorisugari no Hiro さんのレス (2007/02/21(Wed) 18:05)
けん(大学1年)さんが望遠鏡でイオを眺めているとき,公転軌道を「一周」する時間をどうやって計りますか?
「見かけの一周」と「本当の一周」の違いを考えてください.
Re: イオ
けん(大学1年) さんのレス (2007/02/21(Wed) 18:34)
木星の衛星イオは平均42.5時間で木星を1周するので,その間地球は動かないと近似してもいいと思うのですが,地球も動くとして見かけの公転周期を計るのですか?動きがいまいちイメージにならないのです.
Re: イオ
toorisugari no Hiro さんのレス (2007/02/21(Wed) 20:04)
> 地球も動くとして見かけの公転周期を計るのですか?
そうだと思います.
> 動きがいまいちイメージにならないのです.
木星を静止させて,地球とイオだけが動いてる状況を絵に描いて考えたらどうでしょう?
Re: イオ
toorisugari no Hiro さんのレス (2007/02/22(Thu) 14:40)
けん(大学1年)さん,その後どうですか?イメージはつかめましたか?
ところで, > 地球から見たイオの見かけの公転周期と平均値とのずれが最大になるのはいつか. > 「木星と地球を結ぶ直線が地球の公転軌道に接するとき」と答えに書いてありました.
という文章は正しいのでしょうか?私には,答えの状況は「ずれ」が「最小」になるときの条件,としか思えないんですが... (私は木星正面中央にイオが見え,公転して次にまた木星正面中央にイオが見えるまでの時間を(見かけの)周期と考えています.) # あ,問題文には軌道の状況について一言も触れていないので,すべての軌道は同一平面内にある円軌道と考えています.
もし,「問題+答え」が正しいのなら,私の提示した考え方が間違っているかもしれません.
何か私が考え違いをしてるようなら,指摘していただけないでしょうか? > みなさま
Re: イオ
けん(大学1年) さんのレス (2007/02/24(Sat) 17:57)
レスありがとうございます.おかげさまでイメージはつかめました. ですが,僕も,答えの状況は「ずれ」が「最小」になるときの条件となるように思えてしまいました.
以下,僕が思いついた別の考え方を書きます.
木星と地球を結ぶ直線が地球の公転軌道に接するとき,地球の公転速度は,全ての成分が,イオから離れることに使われます.そうすると,イオが一公転する間に,地球がイオに近づく,もしくは離れる距離が最大となります.これは光を迎えに行く,もしくは光から逃げる距離が最大ということになります.この解釈なら答えと一致します.
toorisugari no Hiroさんに教えて頂いた考え方と,上の考え方で,どちらの方が寄与が大きいかという問題になるのでしょうか?
Re: イオ
toorisugari no Hiro さんのレス (2007/02/25(Sun) 15:29)
> これは光を迎えに行く,もしくは光から逃げる距離が最大ということになります.
??? 最大でないときは,みかけの公転周期は真の公転周期から大きくなったり,小さくなったりするのですか?
Re: イオ
けん(大学1年) さんのレス (2007/02/25(Sun) 23:31)
最大でないときは,地球の公転速度のうち,地球がイオに近づく,もしくは離れることに使われる成分の分だけ,公転周期は変わって見えると思います.
Re: イオ
toorisugari no Hiro さんのレス (2007/02/26(Mon) 14:53)
問題が相対論的(あるいは光速が有限)な見地から導き出すのか,そうでないのか文脈を教えてもらわないと何も言えません. また,そのとき,見かけの周期の定義を教えてもらわないといろいろ考えられます.
ともかく,けん(大学1年)さんの理論がよくわからないので,質問です.
木星と地球を結ぶ直線が地球の公転軌道に接するとき,平均からのズレは最小(平均値と同じ)になるのですか?それとも最大になるのですか?
さらに「接する」ときは木星から離れる場合と近づく場合(向き)とありますが,その場合分けもしなければいけません.
ズレが最小になるのなら,どちらも平均値と同じですから,向きによらない理論でなければいけません.
ズレが最大になるとしたら,向きにより,見かけの周期が最大,最小になります.そのメカニズムを知りたいです.
そこら辺を詳しく説明してください.
あと,ズレのオーダー評価を行った方がよいとおもいます.
Re: イオ
けん(大学1年) さんのレス (2007/02/26(Mon) 23:19)
>問題が相対論的(あるいは光速が有限)な見地から導き出すのか,そうでないのか文脈を教えてもらわないと何も言えません. また,そのとき,見かけの周期の定義を教えてもらわないといろいろ考えられます.
光速は有限となっています.見かけの周期については,その言葉が出ているだけで,定義が書いてありません.
>木星と地球を結ぶ直線が地球の公転軌道に接するとき,平均からのズレは最小 (平均値と同じ)になるのですか?それとも最大になるのですか?
最大になると書いてあります.
>ズレが最大になるとしたら,向きにより,見かけの周期が最大,最小になります.そのメカニズムを知りたいです.
そこら辺を詳しく説明してください.
すみません,勘違いをしていました.この理論は忘れて下さい.
Re: イオ
toorisugari no Hiro さんのレス (2007/02/27(Tue) 13:18)
> 光速は有限となっています.
うわあー.こんな大事な情報最初に出してもらわないと困ります.
私の先の議論はすべて意味がないです.(この可能性に気がつかない私も修行が足りませんが..)
つまり,「視点の移動による見かけの周期のズレ(視差)の補正はおこなうものとする.実際は光速が有限なのに,瞬間的に光が伝わると考えることで生じる,周期の「見かけの変化」の議論をせよ.」ですね.
この場合大事なのは観測対象との距離が変化することです. イオが一周する間木星と地球の間の距離がもっとも変化するのは,地球の公転軌道においてどこですか?たぶん2カ所あるはずですが,それぞれの場合で周期の変化の符号を考えてください.
けん(大学1年)さんがおっしゃる「別の考え」はこれに対応しますね. (少々,誤解があるようですが.)
Re: イオ
イオの硫黄のイオン さんのレス (2007/02/28(Wed) 09:02)
横からお邪魔します. これは,木星を公転するイオの運動を「正弦波の発信器」と考えれば良いのではないでしょうか.公転周期が周波数です. そうすれば,観測者が乗った地球が発信器に対して運動するわけですからドップラー効果がおきますよね. つまり発信器の周波数は上がったり下がったりするわけです.その効果が最大となるのは「回答」にあるとおりの条件です. 計算してみると10秒ほど速く・遅くなったように見えるようです.
公転周期を10秒の精度で測定するのは難しいでしょう. でも少しの周期変化が積み重なると,観測できるほどの時間差になるでしょう. 歴史的にはこの時間差が「発見」されて,光速度が有限であることの傍証となったそうです(余談).
Re: イオ
toorisugari no Hiro さんのレス (2007/02/28(Wed) 13:13)
なるほど,たしかにドップラー効果って考えれば自明ですね. イオの硫黄のイオンさん,ありがとうございます.
> 歴史的にはこの時間差が「発見」されて,光速度が有限であることの傍証となったそうです(余談).
- http://www.sci-museum.kita.osaka.jp/~nozo/publication/pb07-137.html
- http://www.quark.kj.yamagata-u.ac.jp/~kato/education/g-education/chapter3.html
- http://keirinkan.com/kori/kori_physics/kori_physics_1/contents/ph-1/4-bu/4-3-1.htm
(pdf) http://www.hc.keio.ac.jp/earth/ssh/jpn/pdf/1623.pdf レーマー(1644−1710)の有名な実験のようですね.知りませんでした.
Re: イオ
zoro さんのレス (2007/02/28(Wed) 19:23)
イオの硫黄のイオンさん,初めまして.
>観測者が乗った地球が発信器に対して運動するわけですからドップラー効果がおきますよね.
私は天文学が良くわからないのですが,イオの木星に対する公転周期とドップラー効果との関係が全然理解できません.もう少し詳しくお教え下さいませんか?
私の感触では,単に公転周期を計るのに「イオ」が木星の後ろから出て来たという時刻の差分(見かけ上の公転周期,というべきか)をグラフにすると周期的に変化する.この現象は,主として地球の太陽に対する公転運動により地球・木星間の距離が変わるのに連れて伝搬時間が周期的に変化し,それに伴い公転周期が異なる様に見えると解釈できると思うのですが....自分では計算してませんが.
なお,理化学辞典によれば,「ドップラー効果」は,「1842年にJ.Dopplerが初めて研究した」とありますが.
Re: イオ
けん(大学1年) さんのレス (2007/03/01(Thu) 00:12)
レーマーは木星の第1衛星イオが木星の裏側に入ったり出たりする時刻を観測する業務につきました.当時の航海技術,通信技術,時計の精度を考慮すると,この食の始まり,終わりの時刻を知ることは地球上の経度(パリとの経度の差)を知る上で必要なことでした.レーマー以前からイオの公転周期(平均で42.5時間)が平均から規則的にずれることに気づいていました.それは衝(太陽・地球・木星が一直線に並ぶ時)から合(地球・太陽・木星と並ぶ時)までは公転周期が平均より長く,合から衝までは平均より短く,その平均からのずれの最大値は約15秒,ずれをその期間で積算すると約20分になる,というものでした.その理由は理解できなくても,将来の食に関する時刻を正確に予言できるので,経度を求めるという目的には支障はありませんでした.
20分というのはどうやって求められるんでしょうか?実際に数値を机上で求めたいわけではなく,レーマーさんはどのように求めたのかということです.
それから,僕も,zoroさんと同じように,地球と木星の距離の変化によってみかけの周期が変わると解釈してます.ドップラー効果での解釈を教えて頂けたら幸いです.
Re: イオ
toorisugari no Hiro さんのレス (2007/03/01(Thu) 02:27)
けん(大学1年)さん,他人の文章を使う(引用する)ときは,出典を明らかにしましょう.
> 地球と木星の距離の変化によってみかけの周期が変わると解釈してます.
同じ考えですよ.
地球と木星が同じ直線上を等速度運動をする(距離が短くなる)場合を考えましょう.真の周期を 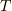 ,光速を
,光速を  ,地球から見た木星の速さを
,地球から見た木星の速さを  とすれば,距離の変化による見かけの周期
とすれば,距離の変化による見かけの周期 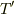 は,それぞれ,
木星のみが動くとして計算すると
は,それぞれ,
木星のみが動くとして計算すると

地球のみが動くとして計算すると

となります.(グラフを描いて確認してください.)
これは音のドップラー効果
と同じですね.(結果も考え方も)
このままでも十分なのですが,さらに進みましょう.
木星が近づくのと地球が近づくのと同じはずなのに,違う式になるのは変ですね.( 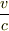 の一次近似では同じですが).
違う式になるのは「移動している系は時間が遅れる」(あるいはどちらから見ても光速が不変)効果を入れていないからです.
の一次近似では同じですが).
違う式になるのは「移動している系は時間が遅れる」(あるいはどちらから見ても光速が不変)効果を入れていないからです.
「静止」している第3者が2者の受け渡しを観測していると考え,上の効果((1)式では 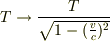 , (2)式では
, (2)式では 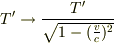 .)を入れて計算すると,どちらも同じ
.)を入れて計算すると,どちらも同じ
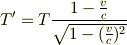
になります.(ここら辺計算したのは久しぶりなので,致命的なミスがあるかもしれません.きちんと考え方や計算を確認してみてください.)
これは光のドップラー効果と同じ式です.(先のURL参照.)
Re: イオ
zoro さんのレス (2007/03/01(Thu) 04:01)
けんさん,
>地球と木星の距離の変化によってみかけの周期が変わると解釈してます.ドップラー効果での解釈を教えて頂けたら幸いです.
もし,そう思っていたのならば,自説を元にして計算を進めるべきだと思います.太陽・地球・木星の相対関係を簡単な円軌道ぐらいに近似して,さらに「太陽・地球・木星」が直線になっている所から,1年分の見かけの周期を計算してみれば良いと思います.きっと,実測値はどこかにあるでしょう.
物理の醍醐味は,ある疑問が出て来たら,それを自分の頭で考えて,解いて行く事ですね.特に自説がでてきたら,最後まで詰めるべきだと思います.この問題で言えば,「(Q1) なんで周期が変わるのか?」と「(Q2) どのような変化が出るのだろう」と2つのポイントがあると思います.
私は,Q1について,なんども考えているうちに,「木星・地球」の距離しか変数として残らないという結論になっていました.で,実際の計算をする為に,軌道パラメータを調べようとした矢先に,イオの硫黄のイオンさんのドップラー効果説をみて驚きました.そこで,自分の考え方を書き,検討してもらいたいと思った訳です.
==== いま,始めからスレッドを拝見していますと,けんさんの質問では,オリジナル問題が完全に引用されていないように感じました.これは,以前の湯川型ポテンシャルの質問にも共通していると思います.
やはり,自分は「何処に書いてある,どんな点」について理解したいと言う事を明確にしないと,回答者は混乱するし,けんさんも,頭のなかで考えている事と,論議している事とに食い違いを生じるのではないかと推察します.
でも,「木星のイオ」という具体的な質問の為に「興味をもった」のも事実で,惑星運動,衛星運動を考える事が出来て感謝しています.ここまで来たのですから,モデル計算を作り,実測データとつき合わす所までやって戴きたいと思います.
#自分で回答を作った後に,それを他人に判り易く説明するのは,とても良い勉強法だとおもいます,キッパリ.
Re: イオ
イオの硫黄のイオン さんのレス (2007/03/01(Thu) 05:41)
皆さん 横からのコメントにレスをありがとうございます. 私の考えはtoorisugari no HiroさんがNo.14668できれいに説明してくれましたので, もう繰り返さなくても良いですよね?あえて若干の補足をしますと, けんさん,zoroさんも,ドップラー効果と同じことをおっしゃられています. ドップラー効果がなぜおきるのか,ということを原理まで追求すれば, 「周期的な現象(たとえば波,あるいは衛星運動)」「現象と観測者の相対運動」 の2つがあれば,どのような場合でも『ドップラー効果』として理解できることになります. 衛星の運動は周期が長いので,いわゆる音や光のドップラー効果と同じであることが わかりにくくなっているのでしょう. というわけで,お邪魔しました.
Re: イオ
zoro さんのレス (2007/03/01(Thu) 10:40)
イオの硫黄のイオンさん,
ご返答有り難うございます.その後,考えた所,お説のようにドップラー効果と同じであることを納得しました.問題を考えていた途中では,相対速度の点からドップラー効果も考えましたが,スペクトルの話では無いと考えて除外しました.
お説の場合,よほど物理の眼力が無いと「自然に出て来る解釈」にならないと感じました.どちらの方が,最終解;イオの公転周期の年周期挙動の計算;といったものを手軽に計算し,説明できるか,だろうとおもいます.
#ただ,天文学を専門的にご研究の方には,簡便に計算できて良いのでしょうね. #そうすると,地球の軌道の接線方向に木星が在るときに一番変動(+/-)が大きいようになるのでしょうか. #でも,軌道モデルや,公転の定義を丁寧に入れようとすると,軌道から直接計算する方が,修正し易くなりそうですね.
ちなみに,地球から木星を見込む角度が変わる為に,イオが出て来る瞬間が変わるような気がしますが,測定にはかからないほど小さいでしょうか?
また,関連して,木星が太陽の向こう側にいるときには,木星を地球から観察できないと思いますが,その期間は何か月ほどでしょうか?さらにイオの木星に対する公転周期を正しく定義するとどうなるかが判らなくなってきました:謎が謎を呼ぶ段階ですね.
このような事は初めて考えたので,宜しければお教え下さいませ.
Re: イオ
yama さんのレス (2007/03/01(Thu) 17:15)
>ちなみに,地球から木星を見込む角度が変わる為に,イオが出て来る瞬間が変わるような気がしますが,測定にはかからないほど小さいでしょうか?
私も同じような疑問を抱きましたが,よく考えてみると,レーマーが観測したのは木星による衛星の食,すなわち衛星が木星の影に出入りする現象なので,それを観測する地球の位置には無関係だと思います.
Re: イオ
zoro さんのレス (2007/03/01(Thu) 18:00)
>レーマーが観測したのは木星による衛星の食,すなわち衛星が木星の影に出入りする現象なので,それを観測する地球の位置には無関係だと思います.
なるほど,「影での出入り」ですか.いま木星をフリーズして,地球とイオだけが動いているとして考えています.もし木星の動きまで考量すると,影も動くので,この手の効果もいれる必要が在りそうですが,明らかに補正項ですね.
たしかに天文学は,軌道計算して終わりの世界でない事は良くわかりました.太陽,地球,木星,イオなどの図を書いていると,宇宙のミニチュアを見ているようで楽しいですね.
Re: イオ
yama さんのレス (2007/03/01(Thu) 22:32)
食の周期から公転周期を求めるには,zoroさんのおっしゃるように影の動きの補正も必要になるでしょう. 簡単な補正としては,木星の1公転の間の食の回数に1回を加えたものが,その間の衛星の公転の回数であると考えることができるでしょう. 他に,木星と衛星の軌道が楕円であるとか,木星と衛星の公転軌道面がずれていることなどによる補正も必要なように思われます.イオの場合はほとんど円軌道ですが,木星の公転軌道面とのずれは3°程度あるようです.
Re: イオ
イオの硫黄のイオン さんのレス (2007/03/01(Thu) 23:10)
皆さん たびたびレスを頂き,ありがとうございます. 実は私は大学で物理を教えている者で,あまりここに出しゃばるのは ちょっと気が引けます.それでもう引っ込もうと思ったのですが, こうして皆さんと掲示板上で会話できるのは愉快ですので,もう一度だけ お邪魔することにしました.
>zoroさん 「物理の眼力」お褒めいただき,ありがとうございます. この眼力が商売道具です.物理の眼力はトレーニングで鍛えられます. 私も時間をかけて少しずつ訓練しました. (ちなみに今は,名前のとおり親父ギャグを愛する中年です)
「地球から木星を見込む角度が変わる為に,イオが出て来る瞬間が変わる」 この点はおっしゃるとおりです.ただしその後でyamaさんがコメント されているとおり,ここでの設問は「影から出る」瞬間を考えていると みてよいでしょう. レーマーの観測も木星の影から出現する時刻の測定です. これには実際的な理由があります. 木星の背後から衛星が現われるのを観測するのでは, 木星が明るいため時刻を正確に測れないのです. 一方,イオなどのガリレオ衛星は木星からかなり離れた位置を 回っていますので,影から出現する場合は,木星の面と離れた位置に 突然現われるように見えます. これは出現時刻の測定が容易です.
では,「木星面からの出現」と「影からの出現」ではどれほど 時間差があるのか? 木星の軌道は地球の軌道の約5倍です. (ミュフ猫さんの計算は,ちょっと?) 太陽−地球−木星が直角三角形を作る場合に時間差は最大となり, 1時間以上も差が出ます. 言い換えれば,木星面からの出現を測定していたのでは, 「見込む角度」を考慮しないと,とんでもなく周期がずれて 観測されてしまう,というわけです.
「木星が太陽の向こう側にいるときには,木星を地球から観察できないと思いますが,その期間は何か月ほどでしょうか?」 これは観測の方法にもよりますが,一般に2〜3ヶ月は観測が困難です. こればかりは天文学者にもどうしようもないでしょうね. ただ,SOHOという有名な太陽観測衛星の画像 (コロナグラフ画像)を見ると,太陽の背景に恒星が写っています. こんな望遠鏡を使えば,きっと何時でも観測できるでしょう.
「イオの木星に対する公転周期を正しく定義するとどうなるかが判らなくなってきました」 これはかなり難しいですが,遠くの恒星を基準にして考えた場合の 回転周期,というところです. 関係して,地球の周りを公転する「月」の公転周期は27.3日ですが, 満月から次の満月までの時間は約2日長い29.5日です. 前者を「恒星月」,後者を「朔望月」と呼びます.
「太陽,地球,木星,イオなどの図を書いていると,宇宙のミニチュアを見ているようで楽しいですね.」 大いに賛成です.
というわけで,長々と書いてしまいました.読んでくださった方, レスを下さった方,ありがとうございました.ここのHPと 掲示板を作った方にも感謝感謝.
Re: イオ
zoro さんのレス (2007/03/02(Fri) 01:01)
イオの硫黄のイオンさん,
なるほど,とても含蓄に富む論議を戴いて楽しかったです.きっと,このスレッドを建てられたけんさんは,色々なヒントを元に計算に四苦八苦しているのだと思います.
>実は私は大学で物理を教えている者で,あまりここに出しゃばるのは >ちょっと気が引けます.それでもう引っ込もうと思ったのですが, >こうして皆さんと掲示板上で会話できるのは愉快ですので,もう一度だけ >お邪魔することにしました.
我が国の伝統かと思いますが,プロフェッショナルとアマチュアはもっと交流を深めても良いのではないかと思います.かのマイケル・ファラデイさんもクリスマスの日に,アマチュア向けの講釈をやったとか....(記憶ちがいでしたらご免なさい)
なにも年に一回のイベントではなくても,このような掲示板で,アマチュアと交流を計る事で,広い意味での物理的基盤の開拓になるように思います.
>この眼力が商売道具です.物理の眼力はトレーニングで鍛えられます. >私も時間をかけて少しずつ訓練しました.
このような発言で,多くの若い方々が「勉強する自信」を得られたと思いますよ.おおいに中年学者さんのご活躍を期待します.
>(ちなみに今は,名前のとおり親父ギャグを愛する中年です)
私は,もうすぐ還暦の老人ですが,数十年ぶりに物理を楽しんでいます.こんどは天文学にも興味が涌きだしています.団塊の世代が,現在の中学/高校/大学などでの教育に協力できるようなシステムを模索したいと思っています(単なるドン・キ・ホーテかも:笑).
>その後でyamaさんがコメントされているとおり, >ここでの設問は「影から出る」瞬間を考えているとみてよいでしょう.
yamaさんがコメントと,これ以降のご解説とから,素人なりにとてもイメージがはっきり取れるようになりました.「黒い影のカーテンからひょこっと顔を出すイオ君」だからですね.
#丁度,イオの硫黄のイオンさんの出現も似た感触でしたよ.
その他,いくつものご解説,有り難うございました.きっとけんさんが計算をおえたら,質問が出て来ると思います.そのときにまた,論議が進展する事でしょうから,それまでは,これ以上の質問はしないで,自分なりに検討させて戴きます.
お気軽に,「物理の眼力」をご披露くださいますように.
Re: イオ
けん(大学1年) さんのレス (2007/03/02(Fri) 16:42)
みなさまありがとうございます. 質問の仕方が下手ですみません.もとの問題と自分の疑問点をちゃんと説明できるよう努力します. 計算を終えたらまた書き込みさせて頂きます.
Re: イオ
zoro さんのレス (2007/03/02(Fri) 19:27)
けんさん,
計算を続けているようで何よりです.
この問題は,天文学としての周期の定義,影から出る瞬間の特異性,円運動間の幾何学が入り組んでいる上に,物理ではあまりお目にかからない,「情報としての伝搬」という事で,経験が少ない1年生の問題としては,難しすぎるようにも思います.
これまでのやり取りから考えて,けんさんはきっとお解きになれると確信しています.でも,判らない事があるならば,途中経過を示して,質問されると良いですよ.また,式の表現が巧く行かない場合,私がLaTeXに書き直ししますから,取り敢えず普通の表現で書いてみてください.
円運動の図はアスキー・アートで書くのは難しいですが,簡単に言葉でいってくれれば,なんとかトライします.
Re: イオ
けん(大学1年) さんのレス (2007/03/04(Sun) 21:23)
>zoroさん
ありがとうございます.今考えているのですが,もう少し頑張ってみます.進展しましたら,また書き込みさせて頂きます.