けん（大学1年） さんの書込 (2007/02/14(Wed) 17:12)

f＝-krの中心力を受けて，ある平面内を運動する質量μの質点の軌跡を求めたいのですが，何から始めればいいのですか？とっかかり方が分かりません． 重力やクーロン力の場合は力の大きさがr^-2に比例していて，本に求め方が載っていたのですが…． よろしくお願いします．

toorisugari no Hiro さんのレス (2007/02/14(Wed) 17:47)

円軌道に限定するのなら，高校レベルでできます．

一般軌道も考えるのなら，まず，方程式を極座標系で書き下し，それを解く必要がありますが，いきなりは無理でしょう．

力学の教科書を参考にしながらわからないことを質問されればいいのでは? ゴールドシュタインの力学などに様々な中心力における解析があるので参考にされると良いでしょう．

ｙama さんのレス (2007/02/14(Wed) 17:59)

中心から質点に向かう単位ベクトルを 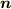とすると，力は と表されます． 一方，質点の位置ベクトルを とすると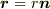， なので，力は 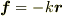と表されます． これに基づいて，x,y成分についての運動方程式をつくるとそれぞれ単振動の式になります．

もちろん極座標で解くこともできます．

toorisugari no Hiro さんのレス (2007/02/14(Wed) 18:03)

そうですね．この問題ならカーテシアンの方が簡単に解けますね． 浅慮でごめんなさい．

けん（大学1年） さんのレス (2007/02/14(Wed) 18:04)

ありがとうございます．ひとまずやってみます．

けん（大学1年） さんのレス (2007/02/14(Wed) 18:41)

極座標の場合，r方向は μ(rの2階微分-rθ1階微分の2乗)＝-kr となりました． θ方向の方程式を利用して，θの1階微分の部分を角運動量Lで書き換えることはできました．でも，続きが分かりません．

軌跡が欲しいのですが，rとθの関係式でなくても軌跡は分かるのですか？

toorisugari no Hiro さんのレス (2007/02/14(Wed) 19:35)

> 軌跡が欲しいのですが，rとθの関係式でなくても軌跡は分かるのですか？

ｙamaさんの方法は試されましたか?

軸座標の方は簡単に解ける微分方程式に変換できないでいるので，いまは直交座標系で考えられたらどうでしょう．

# -----------------------------------------------------------

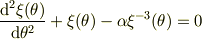
って，どう解くんでしたっけ? >みなさま

nibbana さんのレス (2007/02/14(Wed) 20:29)

>toorisugari no Hiroさん ξ'(θ) --一階微分--を両辺にかけてエネルギー保存の式みたいのを出す，，， という話ではないでしょうか？

りんご さんのレス (2007/02/14(Wed) 22:29)

けんさん，

ちと難しくしすぎましたね．運動方程式は解けているのですよね．

初期条件を ・角運動量の保存，面積速度一定 ・全エネルギの保存← nibbanaさんのコメントと同じでした，失礼しました． に使えば良い様におもいます．

一応，このハンドル名では最後のコメントです．多いに勉強ノーツを増やしてください．

yama さんのレス (2007/02/14(Wed) 23:15)

面倒そうなので計算はしていませんが，極座標で軌跡を表すには楕円積分が必要かもしれませんね．

デカルト座標のほうが計算は簡単だと思います． 互いに直角な２方向の単振動を合成したものになることは容易に分かります． tを消去してx,yの関係式を求めると一般には楕円，特別な場合には円や直線になることが分かります．ただし楕円の主軸が座標軸に一致するとは限りません．

けん（大学1年） さんのレス (2007/02/15(Thu) 02:48)

＞yamaさん，toorisugari no Hiroさん x,y座標でなら分かりました．ありがとうございました．

＞りんごさん 短い間でしたが，ありがとうございました．別のハンドル名を使われることになるのであれば，またご享受頂ければ幸いです．

トンガリ さんのレス (2007/02/15(Thu) 10:55)

名古屋市科学館で30年前に見たのですが， 展示品は，水平に直径1ｍでラッパ状の回転体面が止まっていて，外周に沿って玉が発射される． 玉は始めはゆっくり外周を転がり，円の中心に近づくにつれて速くなり，最後は中心の穴に落ちる． 展示品の面は三次元ですが，引力を重力で代用するのに鉛直軸を使ってしまい，二次元運動を具示する． 展示品の目的は「引力などの中心力を受ける二次元運動の軌跡の具体例を示す」であったと理解する．

「f＝-krの中心力を受けて，ある平面内を運動する質量μの質点の軌跡を示す」展示品を考案しょう． 中心力を重力で代用するのに鉛直軸を使うので，平面は無理ですが，半径の大きな中華鍋の底を使う． 中華鍋の外周に沿って玉を発射すれば軌跡は円運動です．難しくは円錐振動とも言うそうです． 玉を初速ゼロで放すなら軌跡は一平面内の単振動です．斜め向きの初速で発射するなら軌跡は正楕円錐振動です． 中華鍋の真上からビデオ撮影した画像は，f＝-krの中心力を受けて一平面内を運動する質点の軌跡を示す．

半径の大きな中華鍋の底でなくても，玉とそれを吊るす十分長い糸でも展示品を作ることができる． 中心力を重力で代用するのに近似を用いる・・・ので， ?半径の大きな??十分長い糸? を遵守すること・・・かな． 振り子の周期の式の導出に楕円積分に近似を用いるのは確かだが，ここの中心力では近似を用いてない・・・かな． 誰か教えて下さい．

ミュフ猫 さんのレス (2007/02/15(Thu) 11:44)

というか，大学の入試問題で見た気がしますが． 水平で滑らかな床の小さな穴からバネを通して片端に小球を取り付け， もう一方を床から深さL(バネの自然長）の位置に固定して，床の上で小球を いろんな方向に滑らせてその運動を分析するみたいな．ｗ 相当，昔の入試問題だったかと．ちょっと，調べてみようかな．

トンガリ さんのレス (2007/02/15(Thu) 18:17)

バネ定数 k のバネを，中心での伸び零から r 伸ばす仕事は (1/2)kr^2 だから， 中心力を重力で代用するには，鉛直軸は r^2 に比例して高くなければならず， 中華鍋の底が球面では近似であって，底がパラボラの中華鍋が必要ではないか・・・ しかも，中華鍋を転がる小球の重心の成す面がパラボラで・・・

科学館に展示するには正確でなければ，頭が混乱して来たので，少し休みます．

ミュフ猫 さんのレス (2007/02/15(Thu) 18:38)

曲面でやるなら，鉛直線を軸にして，サイクロイド曲線を回転させた回転面 なんかよさそう． ホイヘンスの等時曲線とか最速降下曲線とか言うんですかね？よく知りませんが．

クロメル さんのレス (2007/02/15(Thu) 18:45)

トンガリさんのおっしゃる科学館の展示はラッパ状だったということは，万有引力のポテンシャルｒ＾−１をもしたものだったのですかね．

大きさがあることによって，質点でないことから重心がずれるというのは難しいですね．球を小さくすればすむ問題なんだろうか？

トンガリ さんのレス (2007/02/15(Thu) 20:32)

【単振動と円運動について ２】のスレッドで述べるべきかも知れませんが，

私の考えを総括する． 振り子の円弧振動は運動方程式を解くために近似を用いているので， 「単振動と円弧振動とは切り離して考えた方がよい」 と厳密な先生がみえたのかも知れない．

科学館のラッパ状はとりあえず，万有引力 ｒ^-2 を積分した −ｒ^-1 であつて，御意見を逆さにした面が ラッパを転がる小球の重心の成す面の高さと認識しています．

yama さんのレス (2007/02/15(Thu) 23:47)

鉛直面内のサイクロイド曲線上の運動は，曲線にそって座標をとれば正確に単振動になりますが，それを水平面に射影したものは単振動ではありません． 従って，回転サイクロイド面上の運動を水平面に射影しても，２方向の単振動の合成にはなりません． また，曲面上の運動を水平面に射影したものが万有引力による運動と正確に同じになるようにすることもできません． というのは，一般にこのような曲面上の運動を水平面内の運動と鉛直方向の運動に完全に変数分離することはできないからです．

ただし，曲面の傾きが小さく鉛直方向の運動を無視できる範囲では，適当な曲面上の運動を水平面に射影することによって，中心力場の運動を近似的に再現できます．もちろん，あくまでも近似であって正確なものではありません．