重心速度について
重心速度について
えり さんの書込 (2007/02/14(Wed) 00:48)
「自然長がLでばね定数がkのばねの両端に,大きさの無視できる質量mの粒子を一つずつ取り付ける.二つの粒子は,両者を結ぶ直線上のみを運動する.速度を表すときは右向きを正とする.ばねの長さをL-aまで縮めて,二つの粒子を静かに離すと,二つの粒子は単振動を始める.ばねの長さが自然長と等しく,ばねが伸びつつあるときの左側の粒子の速度を-v0,右側の粒子の速度をv0とする. 次に二つの粒子が上のように単振動しながら,両者の重心が速度?>0で動くような運動を考える.ばねの長さが自然長に等しく,ばねが伸びつつあるとき,左の粒子の速度は?-v0,右側の粒子の速度は?+v0である.ばねと粒子の右側に平らな板をばねに垂直に置いて粒子を反射させる.ばねの長さが自然長に等しく,ばねが伸びつつあるときに,右側の粒子が板にあたって完全弾性衝突をした(板は衝突の際動かない.また,衝突後すぐに板は取り除く).
衝突直後の右側の粒子の速度を?,v0で表せ.また,衝突直後の二つの粒子の重心速度?'を?,v0で表せ」
という問題なのですが,衝突直後の右側の粒子の速度は,-(?+v0)であっていますよね?それで解くと,重心速度は {-m(?-v0)-m(?+v0)}/(m+m)=-?となってv0が出てこないのですが,どこが間違えているのでしょうか・・・(前回の相対速度と似たような質問になっているような気もするのですが)教えてください.お願いします.
それから,私のような部外者が発言する資格はないと十分承知しておりますが,私からのささやかな要望です..毎回,私の質問は初歩的ですが,とてもわかりやすいご指導をたくさんいただけて本当に感謝しています.私もこちらの掲示板を利用させていただいてから(2年目になるでしょうか・・・),物理に対する苦手意識がずいぶん減った気がします.将来私も物理を志す一人として,このような安心して質問できる掲示板はいつまでも存在していて欲しいです.ここの掲示板はすばらしいと思います.これからも変わらぬ運営の方を,どうぞよろしくお願いいたします.
Re: 重心速度について
Joh さんのレス (2007/02/14(Wed) 01:10)
えりさん,こんにちは.
難しい問題ですね.衝突直前では,右の質点は正の向きに,左の質点は負の向きに運動していました.(衝突前の振動は,ちょうど重心をはさんで,左右対称にバネが伸び縮みする感じです.想像できますか?)衝突直後,右の質点は運動の向きを負の向きに変えていますが,左の質点には衝突は他人事なので,さっきと同じく負の向きに速度を持っていると思います.つまり,衝突後は,両方の質点が同時に,右,左,右,左,と振動するようなモードになるのではないでしょうか?
それと,衝突の前後でエネルギーが失われていないことも利用できると思います.
これからかも,遠慮なく掲示板をご利用ください m(__)m
Re: 重心速度について
トンガリ さんのレス (2007/02/14(Wed) 12:28)
「どこが間違えているのでしょうか・・・」と感じたら,先ずは問題を簡単にしたら・・・ 質問ではV>0でv0>0の場合ですが,Vかv0の一方を零として考えると直観できます.
Re: 重心速度について
zoro さんのレス (2007/02/14(Wed) 16:05)
時間がないので,短コメントです.
衝突後の運動量V'はVとは違うはずですね.と言うのも外部の壁との衝突によって運動量の変化分,力積が瞬時に右の質点に対して左向きに与えられるからです.
もう一度,符号に注意して計算を見直してくださいね.物理の式をチェックするためには,なるべく考え方の角度を変えて,現象を説明するといいですね.やはり,静止座標Oxを考えて,
左の質点の速度は,V_L = □ - ○ 右の質点の速度は,V_R = □ + ○
そして,反射板は静止座標Oxに対して静止していることに注意して,右の質点と完全弾性衝突するから, ...
トンガリさんのV=0とするのは,重心系を新たな座標系として乗り移る訳で,強力な検算方法の一つと思います.ただこうすると,反射板が動くに注意してください.
Re: 重心速度について
yama さんのレス (2007/02/14(Wed) 17:21)
衝突は瞬間的に起こり,衝突によって右の粒子の速度は瞬間的に逆転します. しかし,左の粒子の速度は瞬間的にはほとんど変化せず,衝突直後の速度は衝突直前の速度 V-v0 にほぼ等しいと見なせます. なぜなら,衝突したときに左の粒子にはたらく力はばねの力だけであり,瞬間的な短い時間ではその力積はほとんど0です.そのため運動量(従って速度)がほとんど変化しないからです.
Re: 重心速度について
zoro さんのレス (2007/02/14(Wed) 22:55)
夕方,チラッと見て,衝突を挟んで重心速度が保存してるので,慌ててコメントしました.気になっていました(笑).
やはり,この手の問題は,図に書くことです.小さなノートを見開きにして,半分に絵を,逆の半分に式を書く練習をするといいと思います.電磁気もそうですが,絵には符号を付けとくと,検算がとても楽になりますね.本番でも,簡単な絵と符号は小さく書いていたと思います.
また,2体系での「重心運動と相対運動」と「其々の質点座標での運動」を自在に行き来できるようにして置くと良いでしょう.そのためには,上記の「絵」と「式」をやって置くとミスが驚異的に減ります.私は演習を馬鹿にしていましたが,これだけは真面目に練習しました(恥ずかしながら,学部1年生のときですが).
後,衝突現象では,衝突の前後のとても短い時間を考えます.衝突する時刻をTcとでもすれば,t = Tc - ?t 〜 Tc + ?t の時間経過を考えるわけです.ですから衝突の間,他の部分,この場合では,バネやその先の質点の運動はフリーズしていると近似してしまいます.
#衝突自体は,2?tの時間幅より短い運動ですが,運動量の交換をするので, #2体系の重心速度は保存できずに,変化することは大切です. #大雑把な検算には是非とも使ってください.
言い換えれば,衝突の直前の状態が,衝突の直後に変化して,その状態と残りのフリーズした状態から,新たに運動が再開するように考えます.
==== なお,これで「 zoro」のハンドル名では最後のコメントとします.緩急を意識しながら勉強を続けてください.
Re: 重心速度について
えり さんのレス (2007/02/17(Sat) 00:53)
皆様どうもありがとうございました. これは今年の学○院大の問題なのですが,今日早○田でもほとんど同じ問題が出ました(でも時間が足りなくてこの問題には手がつけられませんでした・・・ショック).本命に向けて,もっと精進します!!
Re: 重心速度について
えり さんのレス (2007/02/17(Sat) 01:15)
すみません,やはりまだ疑問点があります..
#衝突自体は,2?tの時間幅より短い運動ですが,運動量の交換をするので, #2体系の重心速度は保存できずに,変化することは大切です.
これのいう「2体系」とは,板と右の粒子の系のことですか?
Re: 重心速度について
zoro さんのレス (2007/02/17(Sat) 01:43)
えりさん,
近くのスレッドで完全回答の是非が問題になったのですが,質問だけ書く,所謂,丸投げ質問に完全回答は教育上望ましくないという結論と思いますし,えりさんも私も,時間的に逼迫しているので,出来るだけ詳しく書いてみます.
>これのいう「2体系」とは,板と右の粒子の系のことですか?
私は,左右の質点を「2体系」と感じています.バネは理想的なので自然長からの差分に比例する「相互作用」と考えて物体と思っていません.
ですから,2体系の「衝突前の重心速度」と「衝突後の重心速度」は保存していない,すなわち変化するといいたかった訳です.
具体的に式で書いたほうが速いです.この時,衝突後の速度は,静止系での個個の質点での速さを出してから,重心系の速度を出すのがいいように思います.
Re: 重心速度について
zoro さんのレス (2007/02/17(Sat) 02:19)
言葉で説明しているとかったるいので式を書いてみます.
衝突前の左右の質点の速度 左の質点の速度は,V_L = V - v0 右の質点の速度は,V_R = V + v0
衝突直後では, 左の質点の速度は,W_L = V_L =V - v0 :そのまま 右の質点の速度は,W_R = -V_R = -V - v0 :静止している理想的な板に完全弾性衝突するから
従って,衝突後の重心速度V'とすると;
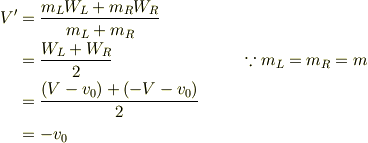
ちなみに重心からみた左右の相対速度は
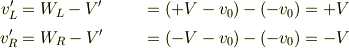
従って,衝突前には,バネが広がる方向で重心に対して最大速度 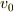 で振動していたものが,衝突後にはバネが縮む方向で重心に対して最大速度
で振動していたものが,衝突後にはバネが縮む方向で重心に対して最大速度  で振動始める.
で振動始める.
また重心速度は,衝突前が  であったものが,方向は逆で大きさが
であったものが,方向は逆で大きさが 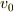 と変化する.
と変化する.
といった感じではないでしょうか.検算はしてないのですが ....
Re: 重心速度について
えり さんのレス (2007/02/17(Sat) 14:39)
すみません,最初の投稿に{-m(?-v0)-m(?+v0)}/(m+m)=-?としていましたが,{m(?-v0)-m(?+v0)}/(m+m)=-D0の間違いです.答案にもこう書いたはずです(汗)
えーと,私もzoroさんのように考えました.そうすると問題文では「重心速度?'を?,v0で表せ」となっているのに?が消えちゃいますよね・・・ということは,消えても平気なのでしょうか..あとは合否結果を待つのみです(笑)
皆様の解説はすごく理解できるので,あとは自分でも類題を探して,積極的に消化していこうと思います.どうもありがとうございました.
Re: 重心速度について
zoro さんのレス (2007/02/17(Sat) 14:52)
>そうすると問題文では「重心速度?'を?,v0で表せ」となっているのに?が消えちゃいますよね・・・ということは,消えても平気なのでしょうか..
題意を「V’= αV +βv0で表せ」と解釈すれば,回答が(α,β)=(0,-1)であるだけと思いますがどうでしょうね.
>あとは合否結果を待つのみです(笑)
全力を賭けて挑戦し,フェアに戦ったら,あとは運命の神様のサイコロを待つだけですね.
自分の手に入った環境を,最大限生かすのが,この次の課題ですね.