無題

home > 掲示板 >

このページのPDF版

サイトマップ

無題

みき　さんの書込 (2007/02/11(Sun) 20:30)

おさわがせしてすみません・・・．もう一問おねがいします！！

磁束密度B[Ｔ]の一様な磁界の中で磁界と垂直な軸の周りに半径a[m] N買い巻きの円形コイルを角速度ω[rad/s] で回転している．コイルに発生する電圧の最大値を求めよ．

Re: 無題

クロメルさんのレス (2007/02/11(Sun) 21:22)

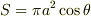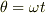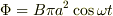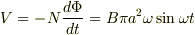磁束密度とコイルの法線方向のなす角をθとおきます．磁束密度の方向からみたコイルの面積は， $S=\pi a^2 \cos \theta$ になりますよね．いま $\theta = \omega t$ という時間変化をさせるので，コイルを貫く磁束は， $\Phi =B \pi a^2 \cos \omega t$ より， $V=-N\frac{d \Phi}{dt} =B \pi a^2 \omega \sin \omega t$ なので，Bπa^2ωですね．

Re: 無題

みき　さんのレス (2007/02/11(Sun) 23:42)

磁束密度の方向から見たコイルの面積として考えるんですね☆ ようやくわかりました☆ ありがとうございました☆

Re: 無題

クロメルさんのレス (2007/02/13(Tue) 01:27)

ここも間違えたか…NBπa^2ωでした．

Re: 無題

トンガリさんのレス (2007/02/13(Tue) 18:03)

「磁束密度の方向から見たコイルの面積として考えるんですね☆」が，私には今いち直感的には理解できません．【コイルを貫く磁束の時間変化に比例して起電力が生じる】かの私の知らない法則を用いてます．これぞ電磁誘導か知らん・・・答えは NBπa^2ωに誤りはありませんが，私の知っている法則で解きたいのです．要領が悪いのは覚悟の上です．

私の知つてる法則は，【コイルが時間あたりに磁束を横切る量に比例して起電力が生じる】と基礎的です．コイルが時間あたりに磁束を横切る量が最大になるのはコイルの平面が磁束密度の方向と一致した時です．

この時，磁束を横切るコイルの長さは：N2πa 磁束を横切るコイルの半円弧の平均速度は：0.5aω 従ってコイルに発生する電圧の最大値：BxN2πax0.5aω＝NBπa^2ω

で辻褄が合いますが，式0.5aωの平均半径0.5aに違和感がないものの，導びき方が分かりません．上記の３式での方法にこだわりませんが，私の言う基礎的な方法での式の求め方を教えて下さい．上記【】かの私の知らない法則についても，成り立つ理由を解説して頂けると幸いです．

Re: 無題

クロメルさんのレス (2007/02/13(Tue) 20:03)

本を調べてみて二つは同じ法則の別の表現であることが分かりました．今回の法則は，一定の磁場中でコイルがうごく場合です．私がつかった 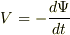$V=-\frac{d \Psi}{dt}$ の法則も【コイルが時間あたりに磁束を横切る量に比例して起電力が生じる】という法則もローレンツ力から来る法則だと分かりました．【コイルを貫く磁束の時間変化に比例して起電力が生じる】はファラデーの法則です．これは，コイルのおかれた空間の磁場の方が変化する場合の法則です．返事を途中まで書いたんですが，明日大学のテスト期間の最終日でやらなくてはいけないことがあるので，詳しくは明日お話しします．

Re: 無題

クロメルさんのレス (2007/02/14(Wed) 20:51)

昨日の続きですね．この現象を定性的にあつかったレンツの法則とは，磁石とコイルを用意して二つを近づけたり遠ざけたりした時コイルにおきる起電力は，コイルのところでの磁場の変化を妨げるように電流が流れるというものです．この法則は次の二つのことをいっています．一つ目は，磁石を動かすとき，つまり磁場の強さが変化する時です．二つ目はコイルが動く時です．私が使った法則は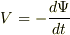， $V=-\frac{d \Psi}{dt}$ という形でこの両方に適用できます．この問題の場合磁場は変化していないので二つ目の法則に適用したことになります．トンガリさんの，【コイルが時間あたりに磁束を横切る量に比例して起電力が生じる】と同じ法則です．つまり，二つは同じ法則の別の表現です．その元になる法則は，ローレンツ力です．式で表すと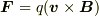， $\bm{F}=q(\bm{v} \times \bm{B})$ です．回路の中の微小な線素を考えます．接線ベクトルを 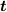$\bm{t}$ ，長さを $\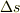Delta s$ とします．ｑの電荷を線素の端から端まで運ぶ仕事は，

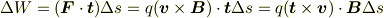
$\Delta W=(\bm{F} \cdot \bm{t})\Delta s=q(\bm{v} \times \bm{B} )\cdot \bm{t} \Delta s = q(\bm{t} \times \bm{v} )\cdot \bm{B} \Delta s$

です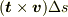． $(\bm{t} \times \bm{v} )\Delta s$ に微小な時間 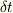$\delta t$ を掛けて速度を距離にしてやると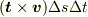， $(\bm{t} \times \bm{v} )\Delta s \Delta t$ ですが，これは，微小時間にこの線素が掃いた面積 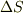$\Delta S$ に等しく，向きはその面の法線方向です．面の法線方向を向いた単位法線ベクトルをｎとします．よって 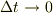$\Delta t \to 0$ の極限をとると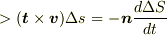， $>(\bm{t} \times \bm{v} )\Delta s=-\bm{n}\frac{d \Delta S}{dt}$ となります．これを曲線全体で積分します．すると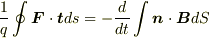， $\frac{1}{q} \oint \bm{F} \cdot \bm{t}ds =-\frac{d}{dt}\int \bm{n} \cdot \bm{B} dS$ この式の左辺はコイルを一周した時の起電力，右辺は磁場をコイルを端にもつ面で積分したものの時間微分です．（時間微分がかかるので，面積分はコイル内全体でも面積の端が変化する所の磁場しか考慮されません．）よって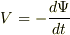， $V=-\frac{d \Psi}{dt}$ が導けました．では，次は実際にこの問題に適用してみます．少々おまちを．

Re: 無題

クロメルさんのレス (2007/02/14(Wed) 22:12)

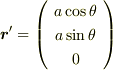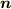座標内に半径aのコイルをおきます．円の中心が原点にくるようにおきます．そして，コイルはｘｙ平面に平行にします．すると円は， $\bm{r}^\prime = \left( \begin{array}{c}a \cos \theta \\ a \sin \theta \\ 0 \end{array} \right)$ で表せます．磁場は，ｘ方向に強さBでかかっているとします．ここでコイルの回転に査読にあげた私の記事 http://hooktail.maxwell.jp/kagi/40a0b8b22d9c875328f706c967f4a930.html を使います．回転軸を表す $\bm{n}$ は，コイルが回転する方向なので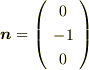， $\bm{n} = \left( \begin{array}{c} 0 \\ -1 \\ 0 \end{array} \right)$ なので，行列Nは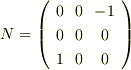， $N = \left( \begin{array}{ccc} 0 & 0 & -1 \\ 0 & 0 & 0 \\ 1 & 0 & 0 \end{array} \right)$ となります．回転する角度は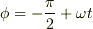， $\phi = -\frac{\pi}{2}+\omega t$ で私の最初の回答の中の $\theta$ と一致します．回転行列 $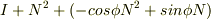I + N^2 +( -cos \phi N^2+sin \phi N )$ は， $\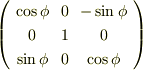left( \begin{array}{ccc} \cos \phi & 0 & - \sin \phi \\ 0 & 1 & 0 \\ \sin \phi & 0 & \cos \phi \end{array} \right)$ ですから，これにｒ’を右から掛けて回転させるとｒになったとすると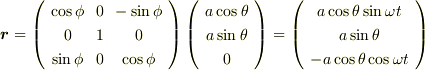， $\bm{r} = \left( \begin{array}{ccc} \cos \phi & 0 & - \sin \phi \\ 0 & 1 & 0 \\ \sin \phi & 0 & \cos \phi \end{array} \right) \left( \begin{array}{c} a \cos \theta \\ a \sin \theta \\ 0 \end{array} \right)= \left( \begin{array}{c} a \cos \theta \sin \omega t \\ a \sin \theta \\ -a \cos \theta \cos \omega t \end{array} \right)$ コイルの速度ベクトルｖはｔで微分して， $\bm{v} = \frac{d \bm{r}}{dt} = \left( \begin{array}{c} \omega a \cos \theta \cos \omega t \\ 0 \\ \omega a \cos \theta \sin \omega t \end{array} \right)$ です．接線方向ベクトルｔはθで微分して長さを１にすれば，

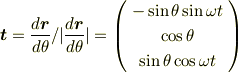
$\bm{t}=\frac{d \bm{r}}{d \theta}/ |\frac{d \bm{r}}{d \theta}|=\left( \begin{array}{c} -\sin \theta \sin \omega t \\ \cos \theta \\ \sin \theta \cos \omega t \end{array} \right)$

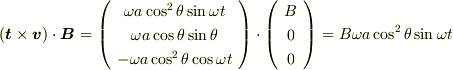です． $(\bm{t} \times \bm{v}) \cdot \bm{B} = \left( \begin{array}{c} \omega a \cos^2 \theta \sin \omega t \\ \omega a \cos \theta \sin \theta \\ -\omega a \cos^2 \theta \cos \omega t \end{array} \right) \cdot \left( \begin{array}{c} B \\ 0 \\ 0 \end{array} \right) = B \omega a \cos^2 \theta \sin \omega t$ これは，ｒという位置にある線素の単位長さあたりの起電力です．これに微小線素の大きさ 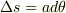$\Delta s = a d \theta$ を掛けて，０から２πまで積分してやれば起電力Vが求まり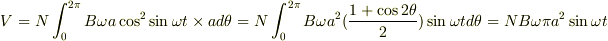， $V = N\int ^{2\pi} _0 B \omega a \cos^2 \sin \omega t \times a d \theta = N\int ^{2\pi} _0 B \omega a^2 (\frac{1+\cos 2 \theta}{2}) \sin \omega t d \theta = NB \omega \pi a^2 \sin \omega t$ です．

Re: 無題

りんごさんのレス (2007/02/15(Thu) 01:08)

クロメルさん，横から失礼します．表示の事です：

●別行の数式のテキスト．Texとしている；改行が少なくとも1つ入れば良いらしい． <Tex> y = ax^2 +bx +c </Tex> ↓

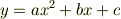
●インラインの数式→<Tex>sin omega t</Tex>

正弦関数 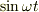$\sin \omega t$ の係数は...．

以上．

Re: 無題

クロメルさんのレス (2007/02/15(Thu) 11:39)

＞りんごさん

なるほど，改行をいれるんですか，そのほうが見やすいですね．ありがとうございました．

Re: 無題

トンガリさんのレス (2007/02/15(Thu) 12:39)

クロメルさん御指導有り難う御座いました．参考になりました．

直感・直観に染まった機械設計者にとっては数式を理解し難い面があります．とは言え，ヒョウタン型の圧力容器の最小直径部に働く引っ張り力の計算では，最小直径部の内側断面積 x タンク内外の圧力差で行い，積分による相殺を要領よく使っている．

今回の問題では，コイルが回転して磁束を横切る量は，コイルが描く面積内の磁束の量の式の微分と関係する・・・感触なので，その方向で，自分でも基礎的に直観的に研究したいと存じます．今回の問題が解決した暁には私も一つ要領がよくなることでしょう．

Re: 無題

トンガリさんのレス (2007/02/15(Thu) 15:10)

１．磁束密度とコイルの法線方向が一致するときのコイルが描く面積をＳとおく．２．時間を t とおくと，磁束密度とコイルの法線方向の成す角は ωt である．３．時間が t のときのコイルが描く面積内の磁束の量はＢＳcos(ωt) である．４．微小な dt 秒後のコイルが描く面積内の磁束の量はＢＳcos(ωt+ωdt) である．５．この dt 秒間にコイルが描く面積内の磁束の量は −ＢＳ[cos(ωt+ωdt)−cosωt] 減った．

６．磁束の量が減ったと言うことは，減った分だけコイルが磁束を横切ったに違いない．

７．コイルが時間あたりに磁束を横切った量は −ＢＳ[cos(ωt+ωdt)−cos(ωt)]／dt ８．これに三角関数の微分の知識を適用して＝ＢＳωsin(ωt) ９．さらに，巻数Ｎと面積Ｓ＝πa^2 を適用して起電力＝ＮＢωπa^2 sin(ωt) を得た．

Re: 無題

トンガリさんのレス (2007/02/15(Thu) 17:25)

電磁誘導に関連して，高校物理の先生のサークルのサイトからのパクリですが，

先日行われた大学入試センター試験の物理?に，ちょっと不適切な設問があった．「鉄心に1次コイルと2次コイルを2:1の比で巻いて，1次コイルに10Vの交流電圧をかけると2次コイルに何Vの交流電圧が生じるか」という設問ですが，

設問図のような棒状鉄心では磁束が漏れて，出題者が期待する 5Vは出ません．実際にやってみるとたったの0.3V，コの字形の鉄心をくっつけてやると2.1V，物理室によくある組立コイルを使うとなんとか4.5Vが出た．受験生を迷わせないように，ちゃんとした問題を作らないといけません・・・

Re: 無題

クロメルさんのレス (2007/02/15(Thu) 17:31)

この問題はコイルの微小部分ごとに違う起電力が発生するので，微分を使うんだろうなと思いといてみました．この解法を読んでいくうえで，必要になるだろう知識がのっている本を私がもっている本の中であげておきます．No.14319は，

「岩波基礎物理シリーズ３電磁気学川村清著ISBN 4-00-007923-9」

からp17〜p23を抜粋しました． No.14321の記事は，特に本を見たわけではありませんが，必要になる知識は分野としては「ベクトル解析」の中の「ベクトルの微分」と「線積分」に関する知識だとおもいます．後はNo.14319の知識だけで読めるはずです．参考になりそうな本として，

「マイベルク/ファヘンアウア工科系の数学４多変数の微積分−ベクトル解析−及川正行訳サイエンス社ISBN 4-7819-0781-1」

があります．この本の最初の数ページにある「接線ベクトル」を用いました．今回曲線を表現するパラメータはθです．この本のパラメータはｔとしてあることを考慮すれば読みやすいかと思います．

これ以上は少し深入りするのですが，最後の 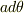$a d \theta$ を掛けて積分するところは，やはりこの本の「線積分」の章を読んでみてください．

参考になればうれしいです．

[home] [掲示板] [ページの先頭]