相対速度で混乱してしまいました
相対速度で混乱してしまいました
えり さんの書込 (2007/02/11(Sun) 13:04)
唐突ですみませんが,混乱してしまいましたので投稿させていただきます.
相対速度は(相手の速度)−(自分の速度)ですよね? そのように考えると,たとえばPの速度は,Qの進行方向の後方で大きさはQより見てuであった場合,(Qの速度はD)Pの速度D'は上の式で表すと -u=D'-D で求められますよね?唐突で申し訳ありませんが,宜しくお願いします.
Re: 相対速度で混乱してしまいました
Joh さんのレス (2007/02/11(Sun) 15:53)
自分と相手の乗っている直線上で,どっちに進む速度を正とするのか,最初にちゃんと決めて考えてみてください.(絵を描くと,もっと分かりやすいと思います.)
Re: 相対速度で混乱してしまいました
zoro さんのレス (2007/02/11(Sun) 21:42)
どこが混乱しているのかが,判りかねますが,此方の感触を書いてみます.
力学の問題では,何は無くても,問題対象を記述するべき適当な慣性系Oxを考えて,そこからみた考察物体の運動を示す量を決めるのだと思います.当然の事として,ニュートンの古典力学の範囲で考える事にします.
この問題では,Qを慣性系Oxについてが先に決め,そのQから見たPの相対速度から,Pの慣性系Oxについての速度を決めるのだと思います.
従って,
・慣性系Oxから見たQの座標の値, 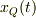 ・慣性系Oxから見たQの速度の値,
・慣性系Oxから見たQの速度の値, 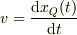 ・Qから見たPの相対速度の値,
・Qから見たPの相対速度の値, 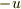 (なぜならば,Pは後方で,その大きさu>0 と考えたとして)
(なぜならば,Pは後方で,その大きさu>0 と考えたとして)
同様にPに付いても,
・慣性系Oxから見たPの座標の値, 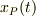 ・慣性系Oxから見たPの速度の値,
・慣性系Oxから見たPの速度の値, 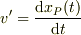 ・Pから見たQの相対速度の値,
・Pから見たQの相対速度の値, 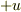 (なぜならば,Qは前方で,その大きさu>0 と考えたとして)
(なぜならば,Qは前方で,その大きさu>0 と考えたとして)
もし,考察している意識がP点に乗っているような場合, 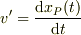 そのものでしょう.
そのものでしょう.
もし考察している意識がQ点に乗っていて,そこからPの速度を考える時には;
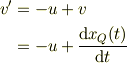
と意識するかも知れませんね.
なにか気になったら,基本に戻りましょう.
【追伸】
上を書いた後,思い出しました.初心者のころ,符号を間違え易かったのです.1次元の時も,わざわざ基底ベクトルを付けて表しました.例えば;
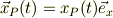
Re: 相対速度で混乱してしまいました
yama さんのレス (2007/02/11(Sun) 23:08)
意味がわかりにくいのですが・・・ 「Pの速度は,Qの進行方向の後方で大きさはQより見てu」ということは,Qから見るとPはQの進む向きと逆向きに速さuで進んでいるということでしょうか? また,Qの進む向きを正の向きとしているのでしょうか? そうだとすると,Qに対するPの相対速度は -u になるので,えりさんの書かれた式は正しいと思います.
Re: 相対速度で混乱してしまいました
りんご さんのレス (2007/02/11(Sun) 23:26)
今一度,追加意見を述べます.
初期条件では,u>0 で始まったものの,衝突などの過程をへてu<0 に混乱を生じるのかも知れないなと思いました.
やはり,計算中は, 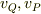 として置いて,最後に相対速度にしてやると善いのかも.
として置いて,最後に相対速度にしてやると善いのかも.
Re: 相対速度で混乱してしまいました
えり さんのレス (2007/02/11(Sun) 23:46)
皆様,どうもありがとうございました. 私も最初,問題文の日本語の理解に苦しんでしまい,なかなか立式できませんでした. 常に座標系のことも忘れずに,考えられるようにしたいと思います. どうもありがとうございました.
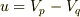 ではないですか?
ではないですか?