静電エネルギー
静電エネルギー
ユウ さんの書込 (2007/02/11(Sun) 12:56)
はじめまして．大学に入って物理を始めた大学１年の者です．レポートでどうしても分からないことがあったので質問させてください！
球殻（半径a,b;a＜b）とし，内側（半径a)を+Ｑ，外側（半径b)を-Ｑの電荷で帯電させた．この系の持つ静電エネルギーを，無限遠方からまず内側の球殻に正の電荷を運び，続いて外側の球殻に負の電荷を移動してくるときに必要な仕事から求めよ．
というものです．ほかの方法で（静電エネルギー密度を用いて）求めた結果，答えは 
だと思うのですが，問題の方法でうまくこの答えが導けません．どのように考えればよいのでしょうか？よろしくお願いします．
Re: 静電エネルギー
クロメル さんのレス (2007/02/11(Sun) 19:35)
こんにちはユウさん．
まず電荷ｑに帯電した球殻の作る電界を求めます．
ガウスの法則より，電荷ｑとその電荷がつくる球の中心からの距離ｒのところでの電界E（ｒ）の関係は，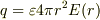 
ですね．
よって，微小な電荷δｑを無限遠から距離ｂまで持ってくるのに必要な仕事は，
![W = \int ^\infty _a E(r) \delta q dr = [ - \frac{1}{4 \pi \varepsilon } \frac{q}{r} ] ^\infty _a \delta q =\frac{1}{4 \pi \varepsilon } \frac{q}{a} \delta q](http://hooktail.maxwell.jp/bbslog/410411c358c7c4df9b15280c2ae5edbd.png)
です．
これをδｑをｄｑとしてｑについて積分すれば，
![U_1= \int ^Q_0 W dq = \int ^Q_0 \frac{1}{4 \pi \epsilon } \frac{q}{a} dq = [ \frac{1}{8 \pi \epsilon } \frac{q^2}{a} ]^Q_0 = \frac{1}{8 \pi \epsilon } \frac{Q^2}{a}](http://hooktail.maxwell.jp/bbslog/658708cb8bb6f8b0bdc27c7c64b3aa37.png)
です．
これで内側の球殻に電荷を持っていく仕事が求まりました．つぎに外側の球殻に負の電荷を運んでいくのですが，このとき内側の静電荷がつくる電界の項を忘れないでください． ![W=\int ^\infty _b (\frac{1}{4 \pi \epsilon } \frac{Q}{r^2} - \frac{1}{4 \pi \epsilon } \frac{q}{r^2}) (-\delta q) dr = [ - \frac{1}{4 \pi \epsilon } \frac{q-Q}{r} ] ^\infty _b \delta q =\frac{1}{4 \pi \epsilon } \frac{q-Q}{b} \delta q](http://hooktail.maxwell.jp/bbslog/a69e4707ac6c01785cfe3ba07fad501a.png)
よってさっき同様に， ![U_2= \int^Q_0 W dq = \int^Q_0 \frac{1}{4 \pi \epsilon } \frac{q-Q}{b} dq = \frac{1}{4 \pi \epsilon b } [ \frac{q^2}{2}-qQ ]^Q_0 = -\frac{1}{8 \pi \epsilon } \frac{Q^2}{b}](http://hooktail.maxwell.jp/bbslog/316daf830fad25180b1a0e3f2eefd54c.png)
より，U1とU2を足せばユウさんの求めた値になりますね．
