よろしくお願いします．

よろしくお願いします．

物理 さんの書込 (2007/02/10(Sat) 23:30)

単振動をハミルトン・ヤコブの偏微分方程式を用いて解け．

です(o≧Д≦))

Re: よろしくお願いします．

クロメル さんのレス (2007/02/11(Sun) 02:06)

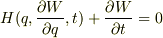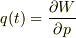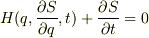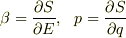ハミルトンヤコビの式は H(q,\frac{\partial W}{\partial q},t)+\frac{\partial W}{\partial t}=0 (1), q(t)=\frac{\partial W}{\partial p} (2)ですね． H(q,\frac{\partial S}{\partial q},t)+\frac{\partial S}{\partial t}=0 (3)をみたすSを満たすSからWの資格をもつものを探します．偏微分方程式(3)の解は２個の任意定数を含みます．そのうち一個はSを解とした時，定数を足しても解となっていることから，この定数はあまり重要ではありません．もうひとつの定数を E とします．（これは考えていくと全エネルギーと分かる） \beta=\frac{\partial S}{\partial E}, \ \ p=\frac{\partial S}{\partial q} (4)とします．ただし 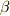\beta は任意定数．なんでもいいから完全解をひとつ得るために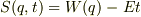， S(q,t)=W(q)-Et (5)とします．すると(1)は 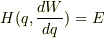H(q,\frac{dW}{dq})=E (6)で，(6)より 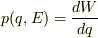p(q,E)=\frac{dW}{dq} 不定積分して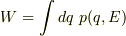， W=\int dq\ p(q,E) (7)を得ます．(5),(4)の第一式より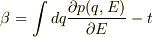， \beta=\int dq \frac{\partial p(q,E)}{\partial E}-t これをｑについてとけば解が求まったことになります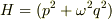． H=(p^2+\omega ^2q^2) より，(6)は 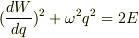(\frac{dW}{dq})^2+\omega ^2q^2=2E よって， \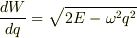frac{dW}{dq}=\sqrt{2E-\omega ^2q^2} ｑで積分した 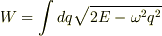W=\int dq \sqrt{2E-\omega ^2q^2} をEで微分して， \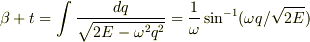beta +t = \int \frac{dq}{\sqrt{2E-\omega ^2q^2}}=\frac{1}{\omega}\sin^{-1}(\omega q/\sqrt{2E}) より， 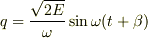q=\frac{\sqrt{2E}}{\omega}\sin \omega (t+\beta) でわかりますか？Σ(・ω・；)