単振動と円運動について
単振動と円運動について
佐藤 さんの書込 (2007/02/09(Fri) 23:08)
掲示板に書き込みさせていただきます.
高校で物理をならっております. そこで質問なんですが 単振動の導入で円運動の射影ということで三角関数で求めることができると知ったのですが なぜ単振動が円運動の射影と同じと見なすことができるのでしょうか?
わかる方がいらっしゃれば,よろしくお願いします.
Re: 単振動と円運動について
Joh さんのレス (2007/02/09(Fri) 23:32)
言葉の定義として,円運動の射影のことを単振動と呼ぶんだと思います.
Re: 単振動と円運動について
クロメル さんのレス (2007/02/09(Fri) 23:41)
どうも初めまして. 円運動の射影は例えばsinθになりますよね.これはsinθの定義からしっくりくると思います. これから三角関数の微分は何かという知識が必要になります. ここで単振動はm(x'')=-kxという方程式に従うというのはいいですか? これをx''=-ω^2xと書き直します.(ω^2=k/m) x=sin(ωt)と置いてみてください.x'=ωcos(ωt), x''=-ω^2sin(ωt)=-ω^2x ですよね.つまり,このxはこの微分方程式の解になっています. 突然サイン関数がでてきましたが,くわしいこのサイン関数の求め方は大学の微分方程式の授業で習うと思います. 結局どんなつながりがあったかというと,等速円運動の性質のうち,そのy座標に注目していると,y方向の加速度がy方向の位置に比例している(m(x'')=-kx)という関係が二つを結びつけているってことです.
Re: 単振動と円運動について
佐藤 さんのレス (2007/02/09(Fri) 23:45)
>Johさん コメントありがとうございます.
すいませんがよくわかりません. ではたまたまばねの運動と円運動が同じだということなのですか? ばねの動きの図と射影したときの図が載っているのですが見ればなんとなくわかるような気がします. だけどばねの運動と円運動が同じように感じることができないもので質問させていただきました.
Re: 単振動と円運動について
佐藤 さんのレス (2007/02/09(Fri) 23:51)
>クロメルさん
コメントありがとうございます.
最初の式の部分はよくわかりませんでした.おっしゃっている意味はわかったつもりですが.
円運動にはそのような性質があるというのはどうやってわかるのですか?
Re: 単振動と円運動について
Joh さんのレス (2007/02/10(Sat) 00:32)
>ではたまたまばねの運動と円運動が同じだということなのですか?
そういうことです.釣り合いの場所から,  だけ伸びた(もしくは縮んだ)場合に,この変位に比例する力を出すバネの場合,比例定数を
だけ伸びた(もしくは縮んだ)場合に,この変位に比例する力を出すバネの場合,比例定数を  とすれば,運動方程式は
とすれば,運動方程式は 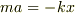 のように書けることは,勉強済みだと思います.
のように書けることは,勉強済みだと思います.
ここで,加速度は 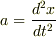 と書けるので,この運動方程式は
と書けるので,この運動方程式は  の微分方程式になります.(微分方程式はまだ習ってないかも知れませんが,変数が
の微分方程式になります.(微分方程式はまだ習ってないかも知れませんが,変数が  だけだというのが,ここでもポイントです.)この微分方程式を解くと,
だけだというのが,ここでもポイントです.)この微分方程式を解くと, 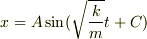 のような解を得ます.
のような解を得ます. 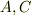 は適当な変数とします.これは,半径
は適当な変数とします.これは,半径 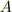 の円上を一定の速度でグルグル回る点の動きの射影に等しいので,最初の命題のようなことが言えたのでした.
の円上を一定の速度でグルグル回る点の動きの射影に等しいので,最初の命題のようなことが言えたのでした.
学校では,きっと微分方程式だとか,微分方程式を解くとかいう話題が,勉強の順序の都合で難しすぎるので,結果だけをいきなり教わったのだと思います.自分で納得したければ,微積分の教科書を勉強してみてください.実際のバネ(つまり,世の中にある色々な本物のバネ)の運動では,空気抵抗があったり,緩衝作用があったり,バネが伸びて馬鹿になってしまったりと,厳密には少し違う運動方程式に従うかも知れないのですが,それでも大抵は,上に挙げた式によって,バネの運動をよく記述することが出来ます.
Re: 単振動と円運動について
クロメル さんのレス (2007/02/10(Sat) 00:56)
「例えば」といったのは,sinθだけでなくcosθも射影になっているからです.
ところで等速円運動の性質ですが,等速円運動は位置ベクトルが 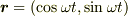 と表されるので,それぞれ成分ごとに微分してやれば,加速度ベクトルは
と表されるので,それぞれ成分ごとに微分してやれば,加速度ベクトルは 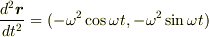 となります.y方向成分だけとると(射影してみると),加速度
となります.y方向成分だけとると(射影してみると),加速度 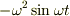 は,位置
は,位置 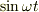 に比例していると分かります.
に比例していると分かります.
Re: 単振動と円運動について
佐藤 さんのレス (2007/02/10(Sat) 16:45)
お返事が遅れてすいません.
Johさんとクロメルさんは同じようなことをおっしゃっているのでしょうか? ということはJohさんがおっしゃっている微分方程式というものを知らないと解決しないということですね.
お二人ともありがとうございました.
それにしてもばねの運動と円運動が同じだなんて不思議ですね.
Re: 単振動と円運動について
yama さんのレス (2007/02/10(Sat) 21:29)
微分方程式を用いない説明をしておきましょう.
半径 r,角速度 ω の等速円運動の加速度の大きさは 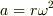 で,加速度の向きは円の中心に向いていることはお分かりのことと思います.
従って
で,加速度の向きは円の中心に向いていることはお分かりのことと思います.
従って 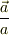 は物体から円の中心に向かう単位ベクトルです.
一方,円の中心を原点としたときの物体の位置ベクトルを
は物体から円の中心に向かう単位ベクトルです.
一方,円の中心を原点としたときの物体の位置ベクトルを 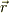 とすると
とすると 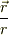 は円の中心から物体に向かう単位ベクトルです.
従って次の関係が成り立ちます.
は円の中心から物体に向かう単位ベクトルです.
従って次の関係が成り立ちます.
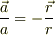 すなわち
すなわち 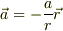 です.
です.
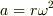 を代入すると次のようになります.
を代入すると次のようになります.
 両辺に
両辺に  を掛け,
を掛け, 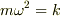 と置くと次の運動方程式が得られます.
と置くと次の運動方程式が得られます.
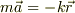 これを成分に分けて表すと次のようになります.
これを成分に分けて表すと次のようになります.
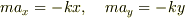 これらはそれぞれx軸またはy軸に射影した運動を表しており,いずれもばねの運動方程式と同じであることが分かるでしょう.
これらはそれぞれx軸またはy軸に射影した運動を表しており,いずれもばねの運動方程式と同じであることが分かるでしょう.
Re: 単振動と円運動について
クロメル さんのレス (2007/02/11(Sun) 00:51)
>佐藤さん そうですね同じこといっていますね.x’というのはxの時間微分という意味です.つまりm(x'')=-kxは微分方程式です.高校生が単振動をならうころには,微分は’で表さなかった気がしたので補足しておきます.
Re: 単振動と円運動について
佐藤 さんのレス (2007/02/15(Thu) 01:39)
遅くなりました.
>yamaさん わかりやすいご説明ありがとうございます.
両方とも中心向きの力ということが類似している理由なんですね.
Re: 単振動と円運動について
しずく さんのレス (2007/02/15(Thu) 21:50)
時刻tとともに変化する(物理にでてくるな)ある量x(t)が x(t)=Xc+Asin(ωt+d)の形で書けるとき, 「ある量x(t) が単振動する」と呼びます. (Xcは振動中心,ωは角振動数,Aは振幅,dは初期位相といいます.) これが単振動の定義です.
だから例えば「電流I(t)が単振動する」ということもあります. (高3の終わりにでてきます).そのときは電流I(t)が I(t)=Ic+Asin(ωt+d)の形で書けることを意味します.
とはいえ,位置x(t)が単振動する例が最も有名で,最も頻繁にでてきますので, 正確には「物体の位置x(t)が単振動する」の意味で, 「物体が単振動する.」と呼ぶことが多いのです.
何かの参考にして頂ければ嬉しいです.