双極子
双極子
nibbana さんの書込 (2007/02/07(Wed) 21:36)
湯川ポテンシャルとδ-関数についての他スレの議論を見ながら双極子について考えていたところ,妙な疑問が出てきたので質問してみることにしました.
以下,真空の誘電率は簡単のため 1 とします. 何度か話題にあがった通り,電気双極子のポテンシャルは
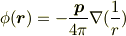
その場合の電荷分布は
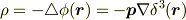
です.それで,「電荷分布がδ-関数の微分ならば,電場にδ-関数的発散が含まれるはず」と考え,電気双極子の電場は,
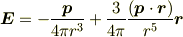
ではなく,例えば
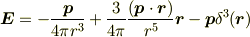
ではないかと.
電気双極子はその大きさが同量の正負の電荷の対ですから,そのあいだにδ-関数的に発散する強い電場が双極子モーメントと逆方向にできる,と考えるのは自然なことのように思われます.間違っているでしょうか? (有限な大きさを持った双極子をひとつ,モデル的に考えたので,後ほど書き込みます.texコマンドをすぐ間違うので書き込むのがひと苦労です.)
Re: 双極子
nibbana さんのレス (2007/02/07(Wed) 23:01)
話のつづきです.
以下のような有限のサイズを持った双極子を考えます.
原点を中心とし,半径 R の球面 S を考えます.球面 S の外部で点状の双極子と同じポテンシャルを仮定し,S上で連続に接続するポテンシャルを内部に設定します.
球面 S の外部 ( r >= R )
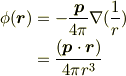
球面 S の内部 ( r < R )
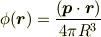
S 上で両者の値が一致するのは簡単に見て取れると思います.また,S の内部のポテンシャルがラプラス方程式を満すのも簡単にわかります.座標の一次なので,2階微分すると 0 ですから.
このモデルで,双極子内部--球面 S の内部--の電場はどうなるかというと,
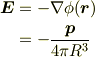
で定ベクトルになります.
---そして,S 内部の電場に対し体積積分 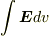 すると,
S の半径 R によらない値,
すると,
S の半径 R によらない値,
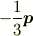
を得ます.
妙なのは係数 1/3 です.色々調べてみるに,*少くともこのモデルに関して*は間違いなどではなさそうです.だからと言って,(点状の)電気双極子の電場は
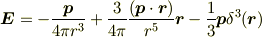
である,というわけでもないでしょう.係数1/3はこのモデル特有のものという気がします.
「電気双極子の電場は原点でδ-関数的発散があるが,その係数は双極子の構成の仕方によるのであって,つまり,双極子を点状とする極限では不定である.」
これで正しい? --これが私の疑問です.
Re: 双極子
りんご さんのレス (2007/02/07(Wed) 23:44)
nibbanaさん,難しい分析で,私には良くわかりませんがコメントさせてください.
次の雑誌,
SGCライブラリ39 マクスウェル方程式 ---電磁気学のよりよい理解のために--- 北野 正雄・著, サイエンス社, 2005-05, ISSN:0386-8257
の「第9章 電気双極子と微小環状電流」の節9.1でデルタ関数による論議,節9.3で粗視化による比較が,考察されています.
もし,ご存知でしたらご免なさい.私も,電磁気学の再勉強がすんだら,このスレッドを勉強したいので,詳しいご検討をお願い申し上げます.
Re: 双極子
nibbana さんのレス (2007/02/08(Thu) 02:16)
>りんごさんへ. 返信どうも.その本は湯川ポテンシャルの話で出てきた参考文献,ですね?見てみます(書店で見つけたら).
なお,δ-関数の扱いの話として,toorisugari no HiroさんやMXKさんの議論とオーバーラップしてきそうな気もしたのですが,極座標のもとでのδ-関数のあつかいとはまた別と考え,新規の投稿にしました.また,本当は磁気双極子での 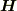 と
と 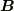 の違いの話でもあります.
の違いの話でもあります.
皆様の意見をよろしく...
Re: 双極子
zoro さんのレス (2007/02/08(Thu) 03:20)
私は,デルタ関数それ自身の数学的な構造に付いての考察によって,物理的な解釈が説明できるとは思えません.
しかしながら,デルタ関数の詳細や粗視化などの詳細を知りません.むしろ点なり,双極子なり,それ以上の多重極における分布を一定微小体積中に分布させて考えた上で,整理して,その後に原型関数(prototype)を吟味しながらデルタ関数を探索するような道を模索したいと感じます.
#おそらく,北野さんの本は,教科書というより,今井さんの「電磁気学を考える」への一つの回答として書かれたのではないかと思います.各章ごとに大胆な切り口があります.今回のスレッドでも,この本と関係が深そうな点が幾つもあるように思います.しかし,この本は雑誌という制限から,初心者にはとても判り難い構造であり,解釈できないような部分もあります.
#物理的な解釈が整備されると,面白い教科書の骨格が出来るようにも感じます.
#なお,私は,北野さんとは面識も無く,連絡もしていません.偶然に拝見した一読者です.より判り易い本があれば,ご紹介頂きたいものです.
勿論,現時点で,数学的にも,物理的にも整理が出来るのならば,ドンドン問題点を解明下さるのは,とても興味深いものです.
>また,本当は磁気双極子でのbm{H}とbm{B}の違いの話でもあります.
この問題は,別途にスレッドを立てられた方が良い様な気がいたします.
Re: 双極子
MXK さんのレス (2007/02/08(Thu) 20:47)
電気双極子の場合には
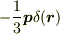 が,磁気双極子の場合には
が,磁気双極子の場合には
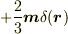 がつくことはいろいろな教科書に書かれています.
モデル依存ではありません.
がつくことはいろいろな教科書に書かれています.
モデル依存ではありません.
Re: 双極子
toorisugari no Hiro さんのレス (2007/02/08(Thu) 22:18)
別解で考えてみました.
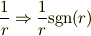
という変換をすると,電束密度 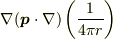 に
に
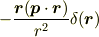
という付加項が出ます.
原点では 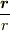 の方向は不定なので,
の方向は不定なので,  を単位ベクトルとして,すべての方向で
を単位ベクトルとして,すべての方向で 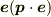 を平均すると,
を平均すると,
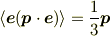
(これは,直感的には,以下の様に考えられます.
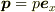 とすれば,
とすれば,
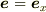 のとき,
のとき, 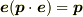
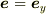 のとき,
のとき, 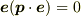
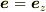 のとき,
のとき, 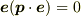 3回に一回だけ非零だから
3回に一回だけ非零だから 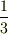 の因子がつく)
の因子がつく)
つまり,
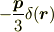
ですね.
Re: 双極子
nibbana さんのレス (2007/02/08(Thu) 22:42)
皆様,レスありがとうございます.ちゃんと返事を書かないといけないのですが,,,
>いろいろな教科書に書かれています.
実を言うと本日,皆さん御推薦の数理科学の別冊がみつからず,何の気なしにジャクソンの電磁気学上巻(吉岡書店)p209に, 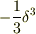 を見つけ,頭の中がグルグルしてまして,,,
"ジャクソン"の数行の説明によると(手もとにないので正確に引用できませんが),
「積分領域を*球状*(太字)の場合」
とか
「(
を見つけ,頭の中がグルグルしてまして,,,
"ジャクソン"の数行の説明によると(手もとにないので正確に引用できませんが),
「積分領域を*球状*(太字)の場合」
とか
「( 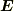 のδ以外の項の)積分は,(角度の積分が0になることから)0と*約束*(太字)する」
などの条件があり,
「注意して扱わないとあいまいな結果になる」
と.
のδ以外の項の)積分は,(角度の積分が0になることから)0と*約束*(太字)する」
などの条件があり,
「注意して扱わないとあいまいな結果になる」
と.
>モデル依存ではありません. とりあえず,"ジャクソン"の説明を見て,必ずしもそう思わなかったのです. ジャクソンは球状領域に話を限定し,そして私のモデルは球形双極子,,,,
なぜモデル依存と考えているか,その説明を一両日中に書いてみます. (,,,もっとも結論がかわるかも?)
>MXKさん "ジャクソン"以外にどんな教科書に書いてありますか? よければ教えてください.
Re: 双極子
nibbana さんのレス (2007/02/10(Sat) 16:58)
双極子の電場 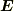 のδ-関数項を,双極子モーメントベクトルを
のδ-関数項を,双極子モーメントベクトルを 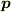 として,
として,
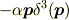
としたとき,係数αが1/3とは限らないのでは,ということを考えるためには,有限な幾何学的大きさをもつ双極子として球ではないものを考える必要があると思うのですが,そういう例として,「平行平板コンデンサー」がずっと頭の中にあるのです.ただ,正確な計算のできるモデルにしたてるのが面倒かも,,,というところです.
仮に「平板モデル」とでも言うことにします.
それぞれ正,負に帯電した面積 S の円板を平行に置き,その極板間隔を  とします.
とします.
 を極板の大きさにくらべ十分小さくとるなら,極板から発生した電気力線のほとんどは極板間に閉じこめられ,ごく一部だけが外部に出ます.
普通のコンデンサーの話と違い,ここでは外部に漏れる電場を無視してはいけません.その"漏れた"電場が双極子の外部にできる電場になるのですから.とはいえ,外部に出る電気力線の本数に対して,内部にとどまる電気力線の本数の比が圧倒的に大きい,あるいは,極板からでる電気力線の総本数に対する,双極子内部の電気力線の本数の比が非常に1に近い.
を極板の大きさにくらべ十分小さくとるなら,極板から発生した電気力線のほとんどは極板間に閉じこめられ,ごく一部だけが外部に出ます.
普通のコンデンサーの話と違い,ここでは外部に漏れる電場を無視してはいけません.その"漏れた"電場が双極子の外部にできる電場になるのですから.とはいえ,外部に出る電気力線の本数に対して,内部にとどまる電気力線の本数の比が圧倒的に大きい,あるいは,極板からでる電気力線の総本数に対する,双極子内部の電気力線の本数の比が非常に1に近い.
荒い(極限的な?)評価として以下のようなことが言えそうです.
正の極板の電荷の総量--極板からでる全電気力線の本数から算出される電荷--を Q とし,また,内部の電場の電気力線の本数から算出される電荷を Q' とします.このとき内部の電場 E は,
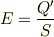
このとき双極子内部での電場の体積積分は,双極子モーメントベクトルと同じ方向にとった単位ベクトルを 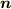 として,双極子の体積が aS であることから,
として,双極子の体積が aS であることから,
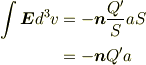
一方で,この平板双極子の双極子モーメントは,正,負の電荷それぞれの総量 Q を使って,
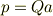
よって,
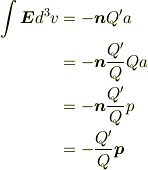
つまり,双極子電場のδ-関数項の係数αは電荷の比 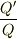 になります.
になります.
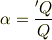
そして,この比はいくらでも1に近い値をとれるから,この「平板モデル」では
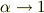
とできる,,,と予想できます.
それで,電場のδ-関数の係数はいろいろに設定できそうなのです. ただ,それぞれに場合に応じて,δ項以外の項に対し,その原点付近での振舞いも何らかの形で規定する必要があるのでしょうね.例えばジャクソンがしているような.
---その点も含め,色々考え中です.
Re: 双極子
MXK さんのレス (2007/02/10(Sat) 21:07)
nibbanaさん
なるほど. デルタ関数の係数が変わると,その分だけ 双極子場の他の項(特に第1項)を(超関数の意味で)補正する必要があるのでは ないでしょうか?
デルタ関数の係数1/3というのは,遠方場を原点まで拡張したときに,電場の渦なし条件が破れるので それを補修するように決まっていると理解しています.
扁平ではなく,縦長にした場合の係数はどうなるでしょう? 1/3でしょうか,0でしょうか?
参考文献ちょっと探しましたが,ここでの議論に間に合うほど詳しいものは 見つかっていません.数理科学別冊を通販ででも入手されるのがいいかも しれません.
1/3のもうひとつの根拠として,双極子場を機械的に求める際の公式
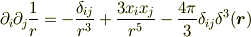
があります.この係数が違っていると
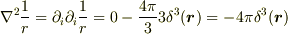 が成り立たなくなります.
(機械的に計算する際に球対称性が暗黙のうちに入っている可能性やこの公式自体の適用限界は否定できませんが.)
この辺は,torisugari no Hiro さんの議論と関係ありそうです.
が成り立たなくなります.
(機械的に計算する際に球対称性が暗黙のうちに入っている可能性やこの公式自体の適用限界は否定できませんが.)
この辺は,torisugari no Hiro さんの議論と関係ありそうです.
#  は
は 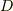 に置き換えた方が分かりやすいと思います.
に置き換えた方が分かりやすいと思います.
Re: 双極子
nibbana さんのレス (2007/02/13(Tue) 17:42)
・・・難しくはないが,面倒な積分計算,極限操作をくりかえし,どこにどんな計算ミスがあるかわかったものではありませんが,この辺で,現状で言えることを書いてみます.
ベクトル場 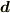 を
を
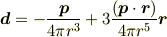
と置きます.このベクトル場は原点を含む体積領域での積分
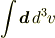
が積分順序によったり,(対数で)発散したりというやっかいな性質をもちます.
また,次のような性質がなりたちます.
原点を含む体積領域を  とし,原点を中心として領域
とし,原点を中心として領域  を
を  倍に相似拡大した領域を
倍に相似拡大した領域を 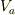 とします.このとき
とします.このとき 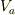 から
から  を除いた中空領域
を除いた中空領域 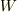 で,
で,
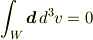
が成り立つ.
原点を含む体積領域  での積分値を何らかの根拠,方法を使い,
での積分値を何らかの根拠,方法を使い,
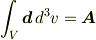
と確定するなら,拡大した領域でも
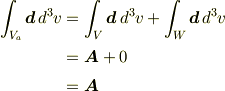
と確定します.
そしてその結果,原点を含むどんな領域でも,その領域に含まれる 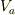 を適当に選び,
を適当に選び, 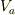 とそれ以外の領域(もはや原点を含まない)にわけて考えることにより,積分値を確定できるようになる.
とそれ以外の領域(もはや原点を含まない)にわけて考えることにより,積分値を確定できるようになる.
電場 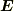 のδ-関数項の係数を決定するというのは,とりもなおさず,体積領域
のδ-関数項の係数を決定するというのは,とりもなおさず,体積領域  をひとつ選び,その領域での積分値を決めることに他ならない.というのもこの領域をε倍した(いくらでも小さな)領域に対しても積分値がかわらないから.
--ただし,積分値あるいはδの係数は,領域の大きさによらなくとも,その(球かあるいは縦横の比が与えられた円筒かといった)形状によって,当然,変ってくる...
をひとつ選び,その領域での積分値を決めることに他ならない.というのもこの領域をε倍した(いくらでも小さな)領域に対しても積分値がかわらないから.
--ただし,積分値あるいはδの係数は,領域の大きさによらなくとも,その(球かあるいは縦横の比が与えられた円筒かといった)形状によって,当然,変ってくる...
自分で試行錯誤するうちに,以上のような話なのだろうとなってきました(つづく).
Re: 双極子
nibbana さんのレス (2007/02/13(Tue) 19:46)
積分値を確定するために仮定することとして,
・双極子は小さいながらも有限な大きさを持ち,原点付近(双極子の内部)で,いろいろな物理量は,深刻な発散をしたりしていない.また,ガウスの定理のような積分公式が原点を含む領域でちゃんと成り立つ.
・系の双極子モーメントは 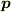 である.
である.
そこで,ある領域中の双極子モーメントは電荷密度ρとして,
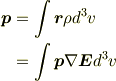
となることから,これを条件として使うことにします.そして部分積分して変形し,表面積分をひねり出す.
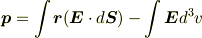
よって,
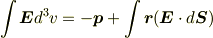
積分領域として原点を含むなんらかの体積領域としたとき,第二項の表面積分は,その原点の扱いが問題な, 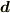 をそのまま使うことができます.表面領域は原点を含まないので.
をそのまま使うことができます.表面領域は原点を含まないので.
このようにして,与えられた原点を含む体積領域  での電場の積分値が,通常の双極子の電場
での電場の積分値が,通常の双極子の電場 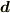 の表面積分から求める,あるいは確定させる,ことができます.
の表面積分から求める,あるいは確定させる,ことができます.
計算の結果:
・原点を中心とする半径  の球形領域では表面積分は
の球形領域では表面積分は 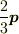 を与え,
を与え,
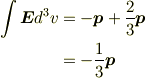
(つまり, 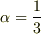 )
)
・原点を中心とする,高さが  ,断面の半径
,断面の半径  の円筒領域では,表面積分は
の円筒領域では,表面積分は
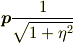
ここで,
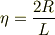
となり, 電場の体積積分は,
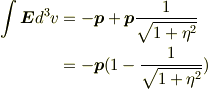
・・・結果を 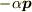 とおいたときの係数
とおいたときの係数  は,
「扁平極限」
は,
「扁平極限」 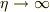 で 1,「縦長極限」
で 1,「縦長極限」  で 0 だったりします.
で 0 だったりします.
いずれも積分値は,領域の形状に依存しても,その大きさによらない値になっています.
今,上の計算に使った球や円筒のような体積領域を  とし,それを原点を中心に
とし,それを原点を中心に  倍に縮小した領域を
倍に縮小した領域を 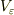 します.そして,「階段関数]
します.そして,「階段関数]
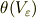
を, 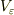 内部で 0 ,外部で 1 の値をとるものとして,
内部で 0 ,外部で 1 の値をとるものとして,
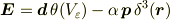
と,書けるということになるかと思います.
#追記:
# 対称性の低い体積領域を選ぶと  は2階のテンソルになるでしょう,きっと.
# 前に書いた球形双極子は,もちろん体積領域として球をとったのと同じ.ただしここでは球の内部の電場を具体的に設定せずに済んでいるのは進歩した点.
なお,
は2階のテンソルになるでしょう,きっと.
# 前に書いた球形双極子は,もちろん体積領域として球をとったのと同じ.ただしここでは球の内部の電場を具体的に設定せずに済んでいるのは進歩した点.
なお, 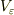 が有限双極子そのものと見るかどうかは自由.
原点にある有限な大きさをもった双極子は
が有限双極子そのものと見るかどうかは自由.
原点にある有限な大きさをもった双極子は 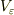 よりさらに小さいと考えても差し支えなし.いずれにしろ最後には,0 とする極限をとることになります.
よりさらに小さいと考えても差し支えなし.いずれにしろ最後には,0 とする極限をとることになります.
(まだつづく)
Re: 双極子
nibbana さんのレス (2007/02/14(Wed) 21:31)
(つづき)
前回の議論をふまえつつ, 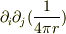 を考えます.まず,球対称な扱い.
を考えます.まず,球対称な扱い.
これは結局は,1/rの代替物--有限化したもの--用意して微分していけば良いのですね..
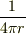 を,次のような関数
を,次のような関数  に置き換えます.
に置き換えます.
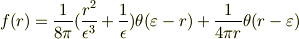
この  は,物理的に解釈するなら,一様に帯電した球のポテンシャルです.球の外では1/r,内部では r の2次関数です.
は,物理的に解釈するなら,一様に帯電した球のポテンシャルです.球の外では1/r,内部では r の2次関数です.
深く考えずにただ微分していくと,
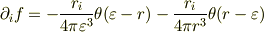
そして,
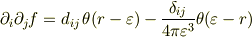
ただし,
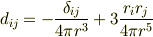
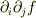 は,最後の項については
は,最後の項については 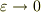 とできて,
とできて,
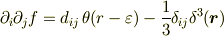
つまり,
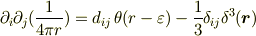
第一項の  が球対称なので,第二項も球対称なのですね.
が球対称なので,第二項も球対称なのですね.
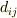 から
から  によって球状領域をすっぽり抜いておき,かわりに
によって球状領域をすっぽり抜いておき,かわりに 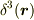 が入る,という構造です.
が入る,という構造です.
(あと一歩,,,)
Re: 双極子
MXK さんのレス (2007/02/15(Thu) 00:46)
nibbanaさん
こんな様子になっているのでしょうか?
電気双極子場
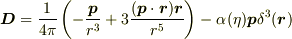 磁気双極子場
磁気双極子場
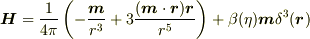 扁平度
扁平度 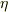 によって
によって
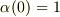 ,
, 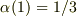 ,
, 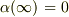 ,
ただし,
,
ただし,
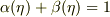 が成り立つ.
が成り立つ.
Re: 双極子
nibbana さんのレス (2007/02/15(Thu) 01:15)
では,*球対称では無いやり方*で, 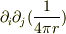 の,原点におけるδ-関数な振舞いを引っ張り出すとどうなる?,,という話.
の,原点におけるδ-関数な振舞いを引っ張り出すとどうなる?,,という話.
この場合,これまでの話を踏まえると,
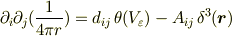
ではないか,と考えられます(これが言いたかったのだ!).
ただし, 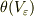 は,原点を含む領域
は,原点を含む領域 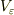 で 0 ,それ以外で 1 な階段関数.また行列
で 0 ,それ以外で 1 な階段関数.また行列 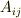 は
は 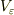 の形状によって決まる二階の対称テンソル.
の形状によって決まる二階の対称テンソル.
全体として球対称性を持ち,第一項が球対称性を持たないならば,第二項も球対称性を持たないはず.ならばクロネッカーのδに比例しないはずだ,ということです.
二つの脚,i,j,を縮約したときに
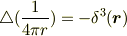
を再現するためには,ただ
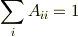
であれば良いです.
それで,何とかして,領域 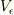 が円筒の場合に
が円筒の場合に 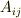 を計算できないかと思ったのですが--せめて球対称でない例をひとつということで,,,,
を計算できないかと思ったのですが--せめて球対称でない例をひとつということで,,,,
1/rに対する代替物を上手に作る,というのは難しそうなので,先に書いた電場の積分に対する考え方で求めていたのです.
先と同じ様に,原点を中心とし,その軸をz軸として,高さ L,断面の半径 R の円筒領域を考える.
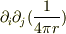 のすべての成分を求めるために,先の電場の積分の話を援用するには,
のすべての成分を求めるために,先の電場の積分の話を援用するには, 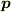 として,x軸,y軸,z軸方向の単位ベクトルをとればよく,また対称性を考慮すれば,そんなにたくさん計算しなくてもすみます.
として,x軸,y軸,z軸方向の単位ベクトルをとればよく,また対称性を考慮すれば,そんなにたくさん計算しなくてもすみます.
結果は--計算間違いや勘違いがなけばですが--,
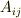 は非対角成分は 0 で,対角成分は,
は非対角成分は 0 で,対角成分は,
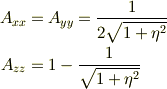
ただし,
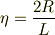
となるようです.
一応,対角成分の和は 1 となります. (やっと一段落.ひとまず話はオワリ)
Re: 双極子
nibbana さんのレス (2007/02/15(Thu) 01:46)
>MXKさんへ. すいません! レスがついているのに気がつかずに次を書いてしまいました.
磁気双極子の場合,磁場 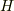 と磁束密度
と磁束密度 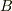 とでは振舞いがことなります.
とでは振舞いがことなります.
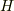 のほうは磁化という湧き出し,吸い込みがあるので,その振舞いは本質的には電場と同じでしょうね.ただ,電場のδの係数が一概にひとつに決められないのと同様,磁場も決められません.不定性の固定をどうするかによりますし,電気双極子と同じ係数を選ぶ必要もないでしょう.--もっとも特に理由がなければ球対称にとるのが常識的だという気はしますが.
のほうは磁化という湧き出し,吸い込みがあるので,その振舞いは本質的には電場と同じでしょうね.ただ,電場のδの係数が一概にひとつに決められないのと同様,磁場も決められません.不定性の固定をどうするかによりますし,電気双極子と同じ係数を選ぶ必要もないでしょう.--もっとも特に理由がなければ球対称にとるのが常識的だという気はしますが.
磁束密度 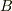 については,その原点でのδ的振舞いの
については,その原点でのδ的振舞いの 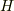 に対する相対的な関係が,はっきり決っています.
に対する相対的な関係が,はっきり決っています.
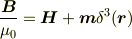
だと思います. 磁場の磁力線は磁石の内部ではN極からS極に走るのに対し,磁束密度のそれはS極からN極に走る,という違いに対応しているのでしょう.
また,ηはあくまで円筒に対する縦横の比です.球の場合には私はηというパラメーターを使っていません.
私の説明はちょっとわかりずらかったり,読みずらかったりするかもしれません. ともかくこれまでわかったことを文字にしないと,と思い,足りないこと,舌足らずなことは,後で追加訂正するつもりで書いています.お許しあれ.
Re: 双極子
MXK さんのレス (2007/02/15(Thu) 18:08)
nibbanaさん,
> 磁気双極子の場合,磁場 |6673e3af11602bdb0a50b72ca29144e9| と磁束密度 |d1bf9890f37d410b52a28f563450a78c| とでは振舞いがことなります.
無理に 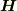 を定義すればそうですが,今,(連続的な)媒質はないので,
を定義すればそうですが,今,(連続的な)媒質はないので,
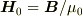 がなりたっており,定数倍の違いしかありません.
わたしが
がなりたっており,定数倍の違いしかありません.
わたしが 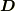 と書いているのも,
と書いているのも, 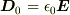 のことです.
のことです.
また,マクスウェル方程式には 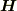 が湧き出しを持つという言明はありません.
が湧き出しを持つという言明はありません.
磁化モデルを想定されているようですが,磁気双極子は小さい電流ループとしてモデル化する方が適当だと思います.
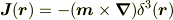
電気双極子の電荷分布
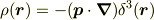
に対応するものです.
Re: 双極子
nibbana さんのレス (2007/02/15(Thu) 19:08)
MXKさんへ.
おっしゃる通りです.磁性体でなく環状電流で考えれば,磁場と磁束密度の振舞いは本質的に同じですね... ただ,微小な磁性体を考えるのも無意味ではないとも思います.
磁気双極子の場合の磁場と磁束密度についても,もう少し考える必要があるかもしれません--電磁気学は,奥が深い.まるでスルメのような味わい...
とりあえず,磁場と磁束密度の違いの件は,今は保留しておきます.
もちろんなにか意見などありましたら,御自由にどうぞ.
Re: 双極子
yama さんのレス (2007/02/16(Fri) 00:46)
電場の源が電荷であるのに対して,磁場の源は磁荷ではなく電流であるという違いが本質的だと思います. そのため,電気双極子が正負の電荷対であるのに対して,磁気双極子は環状電流であるわけです.
ところが,真磁荷(磁気単極子)が存在すると仮定すると,磁荷によって磁場が作られるので,マクスウェル方程式は,磁場の発散が磁荷密度に等しいというように変更されます. そして,正負の磁荷対からなる磁気双極子も存在することになるでしょう. このタイプの磁気双極子による磁場は,正負の電荷対からなる電気双極子による電場に似たものになるでしょう.すなわち,δ関数項の符号が−になるでしょう. また,磁荷の流れすなわち磁流によって電場が生じることになり,環状磁流による電気双極子が存在して,環状電流による磁場と同じタイプの電場,すなわちδ関数項の符号が+であるような電場を生じるでしょう.
もちろん実際には,真磁荷は存在しないので,以上に述べたことは完全な空想ですが,このように空想してみれば,電気双極子と磁気双極子の違いが明確にイメージできるのではないでしょうか.
Re: 双極子
toorisugari no Hiro さんのレス (2007/02/16(Fri) 01:28)
> 磁場の源は磁荷ではなく電流
これと関係あるかわかりませんし,知識があやふやなので間違って存在しない問題を言ってるのかもしれませんが,
観測者が別の慣性系にうつるとローレンツ変換により電場と磁場が変換します. 電荷を動かしても似たようなことがおこります. でも,磁石を動かしてもそのようにならないと聞いた記憶があります.(たしか,z方向に一様な磁場を生む巨大な磁石をx方向に動かしても電場は出てこないだったかな?)(間違ってるかもしれません.)
- そういうことはありますか?
- 仮にそうなら,「磁場の源は磁荷ではなく電流」で説明が付きますか?(単に,磁荷が
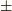 あってうち消してるだけ,という説明でつくのかもしれませんが...)
あってうち消してるだけ,という説明でつくのかもしれませんが...)
「きちんと調べずに質問するのはいけないよ」と言う人がこれで,ごめんなさい.
Re: 双極子
yama さんのレス (2007/02/16(Fri) 07:27)
マクスウェル方程式を真磁荷を含むように拡張することができるという記述を見たことがあるので,そうなると電場と磁場が対称になって磁流によって電場ができるのではないかと思ったわけです. しかし,考えてみると電場は極性ベクトルで磁場は軸性ベクトルなのでそんな単純な話ではないかもしれません.
巨大な磁石を動かす場合ですが,閉じた回路全体としては起電力が生じることはないと思います.しかし,単極誘導の場合を考えると,回路の一部には起電力が生じると思われます.つまり,電場が生じるわけで,その電場はローレンツ変換によって生じるものと考えることができるでしょう.
なお「磁場の源は磁荷ではなく電流である」というのは古典電磁気学の範囲でのことであって,量子力学では当然ながらスピンも磁場の源になりますね.
Re: 双極子
toorisugari no Hiro さんのレス (2007/02/16(Fri) 19:50)
yamaさん,ありがとうございます.
> 巨大な磁石を動かす場合ですが,閉じた回路全体としては起電力が生じることはないと思います.
確認ですが,十分巨大な磁石があり,一様な磁場(z軸方向)が確保されている領域があるとします.
領域内に閉回路をおいたとき,閉回路が領域内にある間, (1) 閉回路をx方向に動かしても,起電力は発生しない. (2) 磁石を-x方向に動かしても,起電力は発生しない. でよろしいのでしょうか.(基本からわかっていないことが露呈していますが...)
同様に領域内に観測者いるとして,観測者が領域内にいる間, (1) 観測者がx方向に等速度運動すると,電場が観測される. (2) 磁石を-x方向に等速度運動させると,電場が観測される. になるのでしょうか?
Re: 双極子
yama さんのレス (2007/02/16(Fri) 22:09)
いずれもその通りだと思います.
Re: 双極子
toorisugari no Hiro さんのレス (2007/02/17(Sat) 19:03)
yamaさん,
> いずれもその通りだと思います.
ですが,私がひっかかっているのは
>> 同様に領域内に観測者いるとして,観測者が領域内にいる間, >> (1) 観測者がx方向に等速度運動すると,電場が観測される. >> (2) 磁石を-x方向に等速度運動させると,電場が観測される.
の(2)です.(2)は間違いと記憶していたからです.
磁石ではなく電磁石で考えてみます.
例えば,z軸を軸に持つ巨大なソレノイドを考えます(半径10m,長さ1000km(?!)).そこに定常電流を流して電磁石にします.
その内部領域では一様な磁場があると考えて良いですね.
(1)の状況だと例えばx方向に等速度運動する電子と,それと一緒に動く系で考えればy軸方向にかかるローレンツ力が電場による力と解釈されて,y軸方向の「電場が観測される」になることはわかります.
(2)の状況はどうなるのでしょう.ソレノイド本体が-x軸方向に動く場合,内部にy軸方向の電場ができるのでしょうか?
たぶん,ソレノイドを円環でなくxy軸に沿った正方形で考えると良いのかもしれません.
x軸に平行な辺はふたつあり,それぞれ逆向きの電流が流れています.このソレノイドをx軸方向に等速度で動かすとこの辺の間に電場が発生するはずですが,その仕組みが理解できません.(速度の足し合わせ,あるいはローレンツ収縮か何かででふたつの辺の電荷密度に違いが出る??!!)
演習書に書いてあるレベルの質問でしたら,文献を教えて下されば幸いです.
Re: 双極子
yama さんのレス (2007/02/17(Sat) 22:49)
等速度運動の相対性を認める限り,(1)と(2)は完全に等価です. 磁石の静止系で一様な磁場が存在していれば,それに対して等速度運動をしている観測者が観測する電磁場は,一様な磁場をローレンツ変換したものになり,その結果電場も観測されることになります.
動くコイルのつくる電磁場を直接計算する場合にも,ローレンツ変換が関係してきます.というのは電荷密度  はスカラーではなく,4次元電流密度ベクトル
はスカラーではなく,4次元電流密度ベクトル 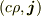 の1成分であって,ローレンツ変換を受けるからです.
正方形ののコイルの場合,コイルの静止系においてx軸方向の1辺の4次元電流密度ベクトルが
の1成分であって,ローレンツ変換を受けるからです.
正方形ののコイルの場合,コイルの静止系においてx軸方向の1辺の4次元電流密度ベクトルが 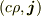 であるとすると,反対側の辺の4次元電流密度ベクトルは
であるとすると,反対側の辺の4次元電流密度ベクトルは 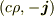 となります.
このコイルがx軸方向に動く場合,2つの辺の電流密度ベクトルがそれぞれローレンツ変換を受けますが,その結果,2辺の電荷密度
となります.
このコイルがx軸方向に動く場合,2つの辺の電流密度ベクトルがそれぞれローレンツ変換を受けますが,その結果,2辺の電荷密度  に差が生じ,その電荷密度の違いによってy軸方向の電場が生じることになります.
に差が生じ,その電荷密度の違いによってy軸方向の電場が生じることになります.
Re: 双極子
MXK さんのレス (2007/02/18(Sun) 16:42)
toorisugari no Hiroさん
運動の相対性から2つの場合を区別することが適当でないことは, yamaさんのご指摘のとおりだと思います.
コイルの系における静磁場は,相対運動する系においてはその一部が電場と して見えるはずです.
相対運動によって磁場が電場にみえたり,逆に電場が磁場にみえたりするのは, すべて相対論的な効果です.数学的にはE と cB が4元2形式をなしていることの帰結です.
(1)の場合に,相対論なしで説明できているように思えるのはローレンツ力の式に,
相対論的効果が含まれているからです. 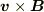 というのはよく
考えてもさっぱり分からない表現です.これって単にまじないのように記憶させられているだけで,
根拠をひとことでいうのはむずかしいのではないでしょうか?
(2)の場合に電場が出ることを納得できれば,(1)の場合も本当に分かったことに
なるのでしょう.わたしも納得してみたい問題のひとつですので,議論をつづけたいと
思います.
というのはよく
考えてもさっぱり分からない表現です.これって単にまじないのように記憶させられているだけで,
根拠をひとことでいうのはむずかしいのではないでしょうか?
(2)の場合に電場が出ることを納得できれば,(1)の場合も本当に分かったことに
なるのでしょう.わたしも納得してみたい問題のひとつですので,議論をつづけたいと
思います.
Re: 双極子
MXK さんのレス (2007/02/18(Sun) 16:54)
> なお「磁場の源は磁荷ではなく電流である」というのは古典電磁気学の範囲でのことであって,量子力学では当然ながらスピンも磁場の源になりますね. 電子のように荷電粒子がスピンをもっている場合は磁場をつくりますが,これも一種の量子的「回転運動」に付随する電流に起因すると考えたほうが適当です. スピンを短絡的に古典的自転だと思うのは危険ですが,少なくとも,電子の頭と尻尾に磁気モノポールが張り付いていると思うよりはマシなモデルだと思います.
Re: 双極子
yama さんのレス (2007/02/19(Mon) 00:21)
簡単な場合について具体的に計算してみます.
ソレノイドではなく,x軸方向に長く延びた長方形のコイルに電流が流れているとします.これは無限に長い2本の平行な直線電流と見なしていいでしょう.
具体的な設定として,xy平面上の直線 y=-L に電流密度ベクトル 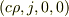 の電流が流れ,同じく直線 y=L に電流密度ベクトル
の電流が流れ,同じく直線 y=L に電流密度ベクトル 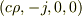 の電流が流れているとします.
これらの電流による磁場は一様ではないので,x軸上の電磁場に限定して考えます.
x軸上では次のようなz軸方向の磁場ができます.
の電流が流れているとします.
これらの電流による磁場は一様ではないので,x軸上の電磁場に限定して考えます.
x軸上では次のようなz軸方向の磁場ができます.
 ただし,Sは導線の断面積です.
ただし,Sは導線の断面積です.
この2本の導線を-x方向に速さvで動かすとします.このとき直線 y=-L 上の電荷密度 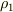 と,直線 y=L 上の電荷密度
と,直線 y=L 上の電荷密度 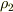 はローレンツ変換の結果,それぞれ次のようになります.
はローレンツ変換の結果,それぞれ次のようになります.
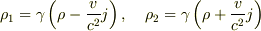 ただし
ただし 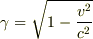 です.
これらの電荷によってx軸上には次のようなy方向の電場ができます.
です.
これらの電荷によってx軸上には次のようなy方向の電場ができます.
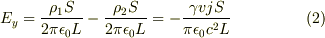
(1)と(2)および 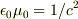 の関係を用いると
の関係を用いると 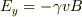 となり,
となり, 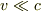 の場合は,
の場合は, 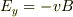 となります.
これはx軸上に
となります.
これはx軸上に 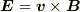 の電場ができることを示しています.ただし
の電場ができることを示しています.ただし  は導線に対する観測者の速度です.
は導線に対する観測者の速度です.
Re: 双極子
toorisugari no Hiro さんのレス (2007/02/19(Mon) 16:10)
yamaさんありがとうございます. よく考えればそうですね.どうも,結論から誘導しようと勇み足すぎました. もう一回ファインマンをよんで勉強し直します.
元ネタを書いてあるような文献が見つからないので,最初の疑問である,「磁石を動かしても電場は発生しない?」の件は一時中断します.
ありがとうございました.
Re: 双極子
toorisugari no Hiro さんのレス (2007/02/19(Mon) 17:53)
MXKさん
> (1)の場合に,相対論なしで説明できているように思えるのはローレンツ力の式に,相対論的効果が含まれているからです. |93cbede669d5129e19879f8cf8323dbb| というのはよく考えてもさっぱり分からない表現です.これって単にまじないのように記憶させられているだけで,根拠をひとことでいうのはむずかしいのではないでしょうか?
自分で使いながら,ローレンツ力を使う議論は変だな.と思っていました.
そもそも,この議論では磁場が変化したとき電場が発生する事の説明はできないからです.でも,こう考えたあと,結局 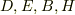 がまだ自分の中で区別できてないなと実感しました.
がまだ自分の中で区別できてないなと実感しました.
電磁気学は本当に難しいですね.
Re: 双極子
toorisugari no Hiro さんのレス (2007/02/19(Mon) 20:18)
> 「磁石を動かしても電場は発生しない?」の件は一時中断します.
まだ,元ネタのほうは見つからないのですが,懲りずに再質問させてください.
先ほどは,ソレノイドの内部での話でしたが,外部ではどうなるのでしょう.
z軸に平行で半無限の長さの,単位長さの正方形断面を持つソレノイドをz<0の空間に一様に敷き詰めて並べます(上からみると格子状,あるいは井桁形状に見えます.).(z>0は真空,z<0はz方向に磁場を持つ電磁石).
これは一個の超巨大なソレノイドと等価であり, 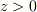 の領域では(十分遠方でも)z方向の一様磁場が観測されますよね.
の領域では(十分遠方でも)z方向の一様磁場が観測されますよね.
このソレノイド群を-x方向に動かしたとき,ソレノイド内部( 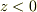 )ではy方向に電場ができますが,
)ではy方向に電場ができますが, 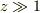 となる位置でy方向の電場は観測されるでしょうか?
となる位置でy方向の電場は観測されるでしょうか?
また,凡ミスだったらごめんなさい.そうでなくても,微妙なオーダーエスティメート(超巨大なソレノイドの幅を  とする)が必要かもしれません.
とする)が必要かもしれません.
Re: 双極子
MXK さんのレス (2007/02/19(Mon) 22:20)
外しているかもしれませんが...
そもそも,ある点での場は,それがどのように作られているかにはよらず,
その値のみに必要な情報が集約されているはずです.
つまり,Aという装置がつくる 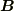 と
Bという装置がつくる
と
Bという装置がつくる 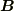 は区別がつかず,相対論的
変換の結果も同じはずです.
は区別がつかず,相対論的
変換の結果も同じはずです.
Re: 双極子
yama さんのレス (2007/02/20(Tue) 00:20)
超巨大ソレノイドについてですが,そのままでは考えにくいので,まず次のようなことを考えてみます. No.14429の例ではx軸上の電磁場についてだけ考えましたが,x軸上からz方向に少しずれた位置での電磁場を考えてみます.この点をA点としましょう. A点はは2本の導線から等距離にあるので,この点にはz軸方向の磁場ができます. 導線を動かすと,2本の導線の電荷密度の違いが生じ,それによる電場ができますが,A点におけるその電場はy方向だけでなく,z方向の成分も持つことになります. しかし,これは電流を担っている電荷だけを考えた場合です.導線中にはこれと反対符号の電荷も存在し,導線に対して静止しています,導線が動いてもこれら静止電荷の密度は2本の導線で差が生じません.そのため,この静止電荷はA点にz方向の電場を生じ,それが,電流を担う電荷による電場のz方向の成分を打ち消します.その結果,A点にはy方向の電場ができることになります. あるいは,反対符号の電荷も含めれば一方の導線には単位長さ当たり+Q,もう一方の導線には単位長さ当たり-Qの電荷が帯電し,それによってA点にy方向の電場が生じるともいえるでしょう.
同様な考え方によって超巨大ソレノイドの場合にも,y方向の電場ができるといえそうです.
なお,No.14429の例で反対符号の電荷を考えなかったのは,x軸上についてだけ考える場合は,それを考慮する必要がなかったためです.
Re: 双極子
ミュフ猫 さんのレス (2007/02/20(Tue) 08:40)
>この静止電荷はA点にz方向の電場を生じ,それが, >電流を担う電荷による電場のz方向の成分を打ち消します.
電流が流れていないときの導線が電気的に中性であるなら, 電流が流れているときの導線は,導線系(つまり,導線が 静止状態にある様に見える観測系)では負に帯電している 様に見えるので,導線系に対するどんな慣性系においても, 電場のz方向の成分は残ると思うのですが.
Re: 双極子
yama さんのレス (2007/02/20(Tue) 10:29)
厳密にいえばその通りだと思います.従って「一方の導線には単位長さ当たり+Q,もう一方の導線には単位長さ当たり-Qの電荷が帯電」というのは厳密には正しくありませんね.
しかしこの場合のz方向の電場は導線が静止しているときに既に存在しているものであって,導線の運動によって新たに生じるわけではありません. 問題になっているのは,導線の運動によってどのように電場が生じるかということだと思いますが,これについては,「導線の運動によってy方向の電場が生じるがz方向の電場は生じない.」と言ってよいと思います.
Re: 双極子
toorisugari no Hiro さんのレス (2007/02/20(Tue) 23:08)
yamaさんありがとうございます.
どうも,私が記憶していたのは 「磁石が動いていても,『磁力線が動く』わけではなく,よって磁石のそばに静止した導線を置いてもローレンツ力(?)による起電力はない」 にすぎないような気がしてきました.それを拡大解釈していたのでしょう.
しかし,磁石が動くことで, 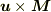 に相当する「双極子」が生まれ,それにより電場が発生するので,
に相当する「双極子」が生まれ,それにより電場が発生するので,
>> 同様に領域内に観測者いるとして,観測者が領域内にいる間, >> (1) 観測者がx方向に等速度運動すると,電場が観測される. >> (2) 磁石を-x方向に等速度運動させると,電場が観測される. >> になる
わけですね.
ありがとうございました.
Re: 双極子
MXK さんのレス (2007/02/21(Wed) 00:25)
電流を動いている系からみると電荷に見えるという ことですが, 以下のように説明できるでしょう.
電流を直線上を速度  で運動する,
等間隔
で運動する,
等間隔  で並んだ電荷
で並んだ電荷  で表す.
電流は
で表す.
電流は 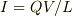 .
同じ間隔で静止して並んでいる
.
同じ間隔で静止して並んでいる 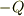 の電荷によって
電気的中性は保たれているとする.
すなわち, 電荷の線密度は
の電荷によって
電気的中性は保たれているとする.
すなわち, 電荷の線密度は
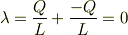
 番目の運動する電荷の世界線は
番目の運動する電荷の世界線は
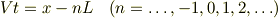
これを速度  で運動する系から見た場合は,
ローレンツ変換によって
で運動する系から見た場合は,
ローレンツ変換によって
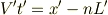
となる. ただし,
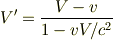
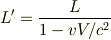
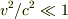 を仮定した.
速度
を仮定した.
速度  だけでなく,
電荷の間隔
だけでなく,
電荷の間隔  が系の運動
が系の運動  によって変化することに
注意する.
静止している電荷の間隔が変わらないことは, 上の式で
によって変化することに
注意する.
静止している電荷の間隔が変わらないことは, 上の式で
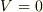 とおけば分かる.
この間隔の違いによって,
とおけば分かる.
この間隔の違いによって,
![\lambda' = \frac{Q}{L'} + \frac{-Q}{L} = \left[1-\frac{vV}{c^2}\right]\frac{Q}{L}-\frac{Q}{L}=-\frac{v}{c^2}I](http://hooktail.maxwell.jp/bbslog/a8845c4d7955febc54b82925d3a64617.png)
のように電流に比例する線電荷密度が発生する.
Re: 双極子
nibbana さんのレス (2007/02/21(Wed) 10:42)
さて,磁気双極子の場合について,その磁場,磁束密度の原点の振舞いについて書こうと思います(話をちゃんと完結させるべく,,,).
結局のところ,磁性体の双極子からはじめることにします.そうすることで,電気双極子の話を援用して済ませることができるからです(後述).
空間に媒質が何も無いときには,磁場 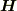 と磁束密度
と磁束密度 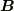 の振舞いは本質的に同じです.ただ,真空の透磁率倍だけの違いしかありません.
の振舞いは本質的に同じです.ただ,真空の透磁率倍だけの違いしかありません.
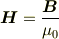
磁性体があるときには,磁気モーメントの分布(磁化)を 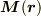 として,
として,
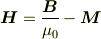
であり,磁束密度が発散を持たない( 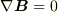 )ので,
)ので,
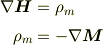
この 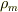 が磁荷です.一様に磁化した円筒(つまり棒磁石)は上面と下面に磁荷があります.
が磁荷です.一様に磁化した円筒(つまり棒磁石)は上面と下面に磁荷があります.
さて,原点に磁気モーメント 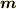 の磁性体(の双極子)があるときには,
の磁性体(の双極子)があるときには,
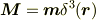
となります.それで磁場と磁束密度の関係は,
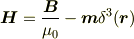
となります.最後のδ-関数が,磁性体(永久磁石)の内部では磁場と磁束密度が逆方向であることに対応し,また,磁場が湧き出しをもつことにも関係しているわけですね.
(今朝はここまで.つづく)
Re: 双極子
toorisugari no Hiro さんのレス (2007/02/21(Wed) 13:00)
> 電流を動いている系からみると電荷に見えるということですが, 以下のように説明できるでしょう.
> この間隔の違いによって, >
> のように電流に比例する線電荷密度が発生する.
この現象, 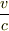 の一次の割には,古典では説明できないみたいですね.どの文献も相対論を使わないとだめだと言っています.
の一次の割には,古典では説明できないみたいですね.どの文献も相対論を使わないとだめだと言っています.
自己弁護するわけではないですが,古典に限った思考で,考えてハマってしまいました.
Re: 双極子
MXK さんのレス (2007/02/21(Wed) 16:35)
toorisugari no Hiro さん
この話,x-t平面に描いてみれば,一瞬で納得できます.
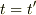 ではなく,
ではなく, 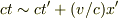 であること(同時性のやぶれ)が効いているのですね.
(ところで,相対論は古典の範疇に入れるのが一般的です.)
であること(同時性のやぶれ)が効いているのですね.
(ところで,相対論は古典の範疇に入れるのが一般的です.)
Re: 双極子
toorisugari no Hiro さんのレス (2007/02/21(Wed) 16:41)
> (ところで,相対論は古典の範疇に入れるのが一般的です.)
^^;
古典 -> 古典力学=ガリレイ共変な力学 に換えておいてください.
(追加) 「非相対論的」と言う言葉を忘れていました.ああ恥ずかしい.
Re: 双極子
nibbana さんのレス (2007/02/22(Thu) 07:16)
磁束密度 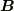 の回転は全電流を与え,磁場
の回転は全電流を与え,磁場 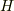 の回転は「真電流」のみ与えます.磁性体しか無いなら真電流は無い.だから,
の回転は「真電流」のみ与えます.磁性体しか無いなら真電流は無い.だから,
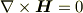
これは磁場 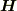 がスカラーポテンシャルを持つこと--いわゆる「磁位」--を意味します.
がスカラーポテンシャルを持つこと--いわゆる「磁位」--を意味します.

このことと先に書いた,
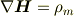
から,磁場は電場と同様な法則に従うことがわかります.つまり,
「磁性体双極子での磁場 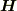 の扱いは,電気双極子の電場
の扱いは,電気双極子の電場 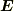 の扱いと同じ」
の扱いと同じ」
なのです.ということは,磁性体双極子では,
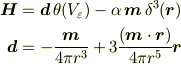
ということになります.磁束密度は,
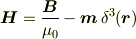
なのだから,
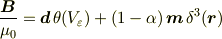
ということがわかります.
ところで,磁性体のみがあるときの磁束密度はいつでも,「磁化電流」

によってつくられると解釈できる.
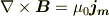
一様に磁化した円筒形の磁性体(棒磁石)に対する磁化電流は,ちょうどその側面を取り巻くコイルの様になります.
ということは,,,
「環状電流の双極子の磁束密度の振舞いは,磁性体双極子の場合と同じ」
なのです!
それで,磁性体双極子の 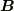 がわかれば,環状電流の双極子の
がわかれば,環状電流の双極子の 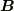 もわかったことになります.
もわかったことになります.
磁場 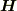 については,環状電流の双極子の場合,
については,環状電流の双極子の場合,
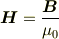
によって,磁束密度 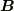 と定数倍しか違いません.この点は磁性体双極子と異なります.
と定数倍しか違いません.この点は磁性体双極子と異なります.
以上.
Re: 双極子
MXK さんのレス (2007/02/22(Thu) 09:08)
nibbana さん
>磁束密度 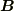 の回転は全電流を与え,磁場
の回転は全電流を与え,磁場 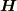 の回転は「真電流」のみ与えます.
>磁性体しか無いなら真電流は無い.
の回転は「真電流」のみ与えます.
>磁性体しか無いなら真電流は無い.
矛盾があるように思います.
ここまでの(磁荷)モデルには電流というものは全く登場していないので,(真電流だけでなく) 全電流もゼロ.したがってBの回転もゼロになってしまいませんか? すると,
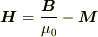
の回転をとると, 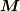 の回転もゼロになってしまいます.
の回転もゼロになってしまいます.
Re: 双極子
yama さんのレス (2007/02/22(Thu) 13:39)
磁性体に磁化電流があるならば,環状電流の双極子でできていることになり,磁荷は0になると思います. 反対に磁性体が磁荷からなる双極子でできているならば,磁化電流は0になると思います.
どうもこの2種類の磁気双極子が混同されているのではないかと思います. このうち,磁荷からなる磁気双極子が実在する証拠は今のところありませんが・・・.
Re: 双極子
ミュフ猫 さんのレス (2007/02/22(Thu) 17:48)
脳みそがとろけそうです.(ToT)
たとえば,絶縁時において電気的に中性な円形の細い導線に, 定常電流が流れているとき,円の中心軸上の電場はどうなる のでしょうか? 円の中心点では,電場は0ですよね?では,中心軸に沿って 少しズレると電場はどうなるのでしょうか? 導線内の負電荷の電荷密度は,大きくなるのでしょうか? 無限直線形状の導線では,電荷の供給が自由なので,単純に 電荷密度をローレンツ変換して,その大きさを比較しました. しかし,円形導線では,勝手に電荷量を増やせません. (もともと,電荷量はローレンツ不変なのですが.w) この場合,どのように解釈すればよいのでしょうか?
Re: 双極子
toorisugari no Hiro さんのレス (2007/02/22(Thu) 18:29)
詳しく理解はしていないのですが.
> 導線内の負電荷の電荷密度は,大きくなるのでしょうか?
円形導線内の負電荷の電荷総量は変わりません.おっしゃるように電荷量はローレンツ不変ですから.
電荷分布に偏りが出るだけです.
ローカルな電荷量の変化については....yamaさん,MXKさんを召喚しましょう. (たぶん,MXKさんの「同時性の破れ」で説明が付くと思いますが..)
Re: 双極子
ミュフ猫 さんのレス (2007/02/22(Thu) 22:48)
>電荷分布に偏りが出るだけです.
なるほど.量子レベルで考えると,導線内の電荷密度は, 一様ではないので,局所的に電荷密度が大きくなる様な モデルを等価にできるのかも. 突き詰めると,静止している正の点電荷と,等速円運動する 負の点電荷が,それぞれ等間隔で円順列を作っているような モデルで説明できるのかな?
Re: 双極子
yama さんのレス (2007/02/23(Fri) 00:13)
無限に長い直線電流の場合は全体の電荷密度が一様に変化することができますが,円電流の場合はそれは不可能です. 円周上に等間隔にN個の電荷が静止していたとして,それが動き出したとします. 動き出す時刻や速度がばらばらであれば,電荷分布は等間隔でなくなり,電荷密度に部分的な差が生じます.しかし,電荷の間隔が部分的に変わっても全体でN個の電荷があることに変わりはなく,全体の電気量は一定に保たれます. 従ってある部分の電荷密度が増加すれば,他の部分の電荷密度が減少することになります.
直線電流の場合,静止している場合と比べて電荷密度に差が生じる原因は「同時性の破れ」で説明できます. 1つの座標系で同時刻に直線上の電荷の間隔を測定しても,別の座標系ではその測定は同時刻ではありません.従って1つの座標系での同時刻の測定値は,別の座標系での同時刻の測定値とは一致しません.それが電荷密度に違いが生じる原因です. 同時性のずれは直線上の遠いところほど大きくなります.このずれがいくらでも大きくなることができるので,電荷の間隔は直線全体で一様に変化することができます. 円周上に電荷が並んでいる場合は,測定時刻が部分的に違ったとしても,一周すればもとの時刻に戻らないといけません.そのため電荷の間隔が一様に変化することはできません.
Re: 双極子
nibbana さんのレス (2007/02/23(Fri) 17:09)
#スレ違いな話は終った御様子...
MXKさん No.14533 >ここまでの(磁荷)モデルには電流というものは全く登場していないので,(真電流 >だけでなく) >全電流もゼロ.したがってBの回転もゼロになってしまいませんか? >すると,
「磁化電流」って何か,一度自分で調べてみては.
yamaさん No.14539
>磁性体に磁化電流があるならば,環状電流の双極子でできていることになり,磁荷は0 >になると思います. >反対に磁性体が磁荷からなる双極子でできているならば,磁化電流は0になると思い >ます.
「磁化電流」って何か,一度自分で調べてみては?
>このうち,磁荷からなる磁気双極子が実在する証拠は今のところありません >が・・・.
「双極子」って何か,もう一度よく考えてみては.
#以降,スレッドの主旨を考えた発言をお願いします.
Re: 双極子
toorisugari no Hiro さんのレス (2007/02/23(Fri) 17:27)
ああ,やっぱり,そのことでしたか.
> #スレ違いな話は終った御様子... > #以降,スレッドの主旨を考えた発言をお願いします. > 「双極子」って何か,もう一度よく考えてみては.
スレッドの考え方や,なにがスレ違いか,「双極子」とはなんぞや,議論の仕方,等で意見の違いはありそうですが,スレ主さんがおっしゃる事ですから,今後,磁気双極子のローレンツ変換等については,このスレッドで発言しないことにします.
別のスレッドを建てますので,この話題はそちらで議論しましょう.> みなさま
ご不快にさせてもうしわけありません. > nibbana さま
Re: 双極子
MXK さんのレス (2007/02/23(Fri) 18:35)
nibbanaさん
当初より,興味深い議論だと思い,スレッドに参加させていただいていましたが, 不愉快な思いをさせているとは全く気づきませんでした. おわびして,撤退します.
>「磁化電流」って何か,一度自分で調べてみては. 分かっているつもりです. ただ,それは思っておられるほど,普遍的な概念ではないですよ.
Re: 双極子
yama さんのレス (2007/02/23(Fri) 22:35)
余計なお節介だったようですね. すみませんでした.
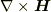 はどうなるのでしょうか?
それから,「磁荷」の単位は
はどうなるのでしょうか?
それから,「磁荷」の単位は 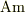 になるんですね.
になるんですね.