角運動量，モーメントについて

けん（大学1年）さんの書込 (2007/02/07(Wed) 14:17)

3つお願いします．

１．慣性系に原点Oをとります．質量mの質点の位置ベクトルをr，原点に対する運動量をpとします．動いている点Aの位置ベクトルをra，原点に対する運動量をpaとします． Aの周りの角運動量は(r-ra)×(p-pa)だと思うのですが，点Aというのが質量のない点の場合，(r-ra)×pでよいのですか？

２．慣性系に原点Oをとります．質量mの質点の位置ベクトルをr，慣性系での働く力をfとします．加速度運動している点Aの位置ベクトルをraとします．このとき，Aの周りの力のモーメントは(r-ra)×(f-mα) （αは点Aの加速度ベクトル）（-mαは慣性力）でよいですか？

３．質点n個の多粒子系において，i番目の質点の質量をmi，位置ベクトルをri，miに働く力をfiとします．重心の位置ベクトルをrGとします．このとき，２．での(r-ra)×(f-mα)において，点Aを重心Gとし，質点n個の和をとると， Σ(ri-rg)×(fi-miα)=Σ(ri-rg)×fi となりました．重心の周りの力のモーメントは，左辺，右辺のいずれで定義されるのですか？

よろしくお願いします．

Re: 角運動量，モーメントについて

りんごさんのレス (2007/02/07(Wed) 15:20)

ご質問の内容が把握できないので，先ずは問い1についてコメントします．

原点Ｏを座標原点にもつ慣性座標系，Oxyzから見た，質量mの位置ベクトルや運動量ベクトルは

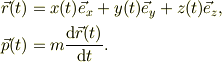
$\vec r(t) &= x(t)\vec e_{x} + y(t)\vec e_{y} +z(t)\vec e_{z}, \\\vec p(t) &= m \frac{\mathrm{d} \vec r(t)}{\mathrm{d} t}.$

同様に点Aの位置は

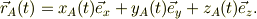
$\vec r_{A}(t) &= x_{A}(t)\vec e_{x} + y_{A}(t)\vec e_{y} +z_{A}(t)\vec e_{z}.$

従って，点Aから質点mの運動を見るとすれば，

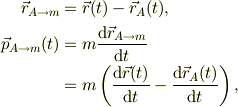
$\vec r_{A \to m} &= \vec r(t) -\vec r_{A}(t),\\\vec p_{A \to m}(t) &= m \frac{\mathrm{d} \vec r_{A \to m} }{\mathrm{d} t}\\&= m \left( \frac{\mathrm{d} \vec r(t)}{\mathrm{d} t} -\frac{\mathrm{d} \vec r_{A}(t) }{\mathrm{d} t}\right),$

といった座標変換的に出すだけだとおもいますが．

ただし，点Aが加速運動をするような場合は，とても計算が難しくなり，解釈もケース・バイ・ケースになってしまうように思います．

Re: 角運動量，モーメントについて

けん（大学1年）さんのレス (2007/02/08(Thu) 13:25)

ありがとうございます．

本では，ある点周りの角運動量，力のモーメントを求めるときに，その点が加速度運動をしていないのですが，加速度運動をしている場合も含めて角運動量，力のモーメントの一般的な定義を知りたいのです．

Re: 角運動量，モーメントについて

りんごさんのレス (2007/02/08(Thu) 13:49)

>その点が加速度運動をしていないのですが，加速度運動をしている場合も含めて角運動量，力のモーメントの一般的な定義を知りたいのです．

良い機会だと思うので，ご自分で一般的な場合に拡張する事を示されては如何ですか？ただ，加速系を一般的にする場合，エレベータのように並進的加速だけでなく，地球の自転のような回転運動も在りますよね．

まず，そこらの加速系の表現も含めて数学的なツールを準備する事もお忘れなく．

どこかで疑問が出たら，書き込んでくださいね．

それと，加速系から見た計算を細かくする前に，先ずは「質点系の力学」をがっちり把握される事をお勧めします．易しい条件での解析法とか方法論をきちんと身に付けて，さらに興味のある点をご自分で掘り下げる方が効率よい勉強になると思いますから．

そのときの勉強ノートをこちらで公開するのも面白いかも知れませんよ．

Re: 角運動量，モーメントについて

けん（大学1年）さんのレス (2007/02/09(Fri) 23:42)

そうですね．上の２と３は合っていますか？等速度運動のときよりは一般化させたつもりなのですが…．

Re: 角運動量，モーメントについて

りんごさんのレス (2007/02/10(Sat) 00:15)

>良い機会だと思うので，ご自分で一般的な場合に拡張する事を示されては如何ですか？ただ，加速系を一般的にする場合，エレベータのように並進的加速だけでなく，地球の自転のような回転運動も在りますよね． > >まず，そこらの加速系の表現も含めて数学的なツールを準備する事もお忘れなく．

私の見解は，上に述べたようです．けんさんの疑問の疑問に，けんさんのベクトル解析が追いついていないのだろうと思います．何となく近い答えを書いても，けんさんの意図する一般的な解にはならないと思います．

以上は私の見解ですが，他の方に善い回答が在る可能性は否定できません．ご意見在ればお願いします→ご専門の方々様．

Re: 角運動量，モーメントについて

りんごさんのレス (2007/02/10(Sat) 14:08)

何度も質問を拝見しましたが，「何が知りたいかが不明です」．

でも，そのような状況に膠着されているのも大変だと思いますので，関連発言をします．これが回答にはならないと思いますが，考えて行く為のヒントになるかも知れませんので．

そこで，問い2.に関連して意見を述べます．基本は，No.14121への補足です．

>慣性系に原点Oをとります．質量mの質点の位置ベクトルをr，慣性系での働く力をfとします．

従って，原点Ｏを座標原点にもつ慣性座標系，Oxyzから見た，質量mの位置ベクトルや運動量ベクトルは；

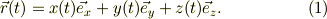
$\vec r(t) &= x(t)\vec e_{x} + y(t)\vec e_{y} +z(t)\vec e_{z}. \tag{1}$

同様に点Aの位置は

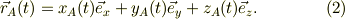
$\vec r_{A}(t) &= x_{A}(t)\vec e_{x} + y_{A}(t)\vec e_{y} +z_{A}(t)\vec e_{z}. \tag{2}$

従って，点Aから質点mの運動を見るとすれば，点Aを原点とする新たな座標系，Ax'y'z'から運動を記述する事になりますが，この系Ax'y'z'は慣性系でないので，このでの位置座標，

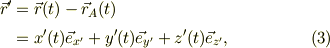
$\vec r'&= \vec r(t) -\vec r_{A}(t)\\&=x'(t)\vec e_{x'} + y'(t)\vec e_{y'} +z'(t)\vec e_{z'}, \tag{3}$

を慣性系から座標変換をして，慣性系Oxyzで得た運動の式を，この座標系で表現し直す必要があります．すなわち，単に元の式を形式的に書き換えてはいけないのです．

また注意すべきは，加速系では，デカルト座標系と違い，基底ベクトルも時間の関数になってしまう事になります．大きな振り子が24時間で振動面が回転するのは有名ですね．この例でもお分かりになるように，加速座標を考えるときには，具体的に考えないといけません．

すこし具体的に考えましょう：電車でいえば；

●直線線路では，並進加速だけでいいでしょうが，

●ある半径の円周では，定速で進行するだけで，加速系になりますし，（これもレッキトした加速系ですが，運動エネルギーの増加が無い，という意味で特殊ですが）

●ある大きな回転台の上で進行している（これは基底ベクトルが，明らかに時間の関数で変化する）

このようにある運動を考える時，運動方程式を与える事と座標を決めることは，別別の問題だと，私はおもいます．

従って，そう気楽に一般論は書けない訳だろうと思うのです．

もし，どうしても，それがしたければ，広い意味での「並進加速」＋「回転運動」を表現する回転座標系の取り扱いになれる必要があります．

で，元の慣性系での運動の式を考えますと，題意より

$\frac{\mathrm{d}}{\mathrm{d} t}\left(\frac{\mathrm{d} m \vec r(t)}{\mathrm{d} t}\right) = \vec f(\vec r,t) \tag{4}$

ここで，定義として，運動量ベクトルとか角運動量として

$\vec p &= \frac{\mathrm{d}m\vec r(t)}{\mathrm{d} t}, \tag{5}\\\vec l &= \vec r \times \vec p, \tag{6}$

を考えると，見通しの善い関係が得られますが；

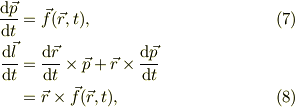
$\frac{\mathrm{d} \vec p}{\mathrm{d} t} &= \vec f(\vec r,t), \tag{7}\\\frac{\mathrm{d} \vec l}{\mathrm{d} t} &= \frac{\mathrm{d} \vec r}{\mathrm{d} t} \times \vec p + \vec r \times \frac{\mathrm{d} \vec p}{\mathrm{d} t} \\&= \vec r \times \vec f(\vec r,t), \tag{8}$

これも，慣性系を使うからですよね．非慣性系にこれらの法則が，そのままの形式で，適応できるかは別問題だと思います．

なお，質点系では，・２質点間の相互作用が2体力であること，・その作用・反作用が大きさが同じで・方向が逆を仮定するだけで，各種の保存法則と関連付ける事が出来ますね．

お恥ずかしい事に，現時点では力学や解析力学の本を手元に持っていません，従ってこれ以上詳しい助言は出来ません．やはり，ベクトル解析，力学の基本をマスターした上で，これ以上先を考察される事を強くお勧めします．

また年寄りくさい考え方かも知れませんが，物理法則を論じるときには，どうしても分数，微積分，ベクトルの表現が多発します．ASCII文字ではどうしても，見る側に強い負担を掛けます．書いている時は，ASCII文字でも意外と書けますが，いざ自分で読み返そうとすると判らなくなります．その点，この数式掲示板のLaTeXは，現時点では，見易い環境だとおもいます．ぜひともLaTeX使いになることをお勧めします．

Re: 角運動量，モーメントについて

けん（大学1年）さんのレス (2007/02/10(Sat) 22:26)

いつもありがとうございます．回転運動の加速度，非慣性形への座標変換などについてあまり知識がない状態では，あまり一般化できそうにないことが分かりました．疑問ノートを作って，そこに書いておこうと思います． LaTeXですが，もうすぐ春休みなので，時間ができたら，使う練習をしてみようと思います．

[home] [掲示板] [ページの先頭]