組み合わせの問題

やかんさんの書込 (2007/02/05(Mon) 13:35)

メンバーのやかんです．ご無沙汰してます．最近寒さで筋肉の血流が悪いせいか，肩凝りがひどく，嫌になっちゃいます．年はとりたくないものですね :)ところで昨日，中２の息子の参考書（受験研究社の自由自在，物理でなく数学）を見ていたのですが，むか〜しから持っていた疑問が噴出しました．例題に，

１から４までの数字が書いた封筒に，それぞれ封筒と同じ数字が書いてあるカードが入っているが，これを入れ替えて，封筒の数字と，入れたカードの数字がすべて異なるようになる組み合わせは何通りか？

という問題が載っていました．解答には，樹形図を描いて，１２３４の封筒に順に２１４３，２３４１，２４１３，３１４２，３４１２，３４２１，４１２３，４３１２，４３２１の９通り！と書いてありましたが，なるほど，数え上げれば，テストでは満点だとは思うのですが・・・．１から５までの場合を自分で試してみたところ，４４通りでした（間違えてなければ）．しかし，自分が中学で習った時から思っていたのですが，なんかこう，樹形図描くって，掛け算を足し算でやっているような，原始的なような・・・．もし１からnまでだったらどうするんだろう？？(^^;この問題もそうですが，よく，ゼロ入りで3桁の整数は何個できるかとかいう問題ありますよね？すべて樹形図なしで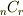， _n C _r とかで解けないもんでしょうかね？ちなみに私が最初の問題でやってみたのは，答え(A)がnの３次式になると仮定して 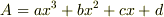A=a x^3+b x^2+cx+d にn=1,2,3,4の場合を代入して，やってみたのですが，n=5で・・・，合わないなあ・・・．無理でしょうか？（これは宿題やレポートではないので（単にやかんの興味なので），もしお時間とご興味のある方がいらっしゃいましたらお教え頂ければ幸いです(^-^)）

Re: 組み合わせの問題

toorisugari no Hiro さんのレス (2007/02/05(Mon) 19:23)

おもしろそうだったんですが，理論的にはつらい．．．しょうがないので，数値計算の結果から類推してみました． <pre> N a_N a_N/(N-1) 1 0 - 2 1 1 3 2 1 4 9 3 5 44 11 6 265 53 7 1854 309 8 14833 2119 9 133496 16687 10 1334961 148329 11 14684570 1468457 12 176214841 16019531 </pre> これから

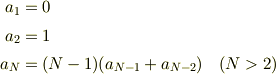
$a_1 &= 0\\a_2 &= 1\\a_N &= (N-1)(a_{N-1}+a_{N-2}) \quad(N>2)$

と予測できます．これを理論的に導く考え方，および具体的な式はほかの方にお願いします．

Re: 組み合わせの問題

サボテンさんのレス (2007/02/05(Mon) 20:23)

封筒の問題ですが，この問題は多項式では解けないと思います．もう1つの漸化式を挙げておきます．これを解くことは私の力ではできませんでした． n-k個を同じ数字の封筒に入れるとして，k個を異なる数字の封筒に入れる並べ方を全て足して，全部の並べ方n!から引きます．

すると，a_n=n!-1-Σ_{k=2〜n-1}n_C_k・a_k です．

Re: 組み合わせの問題

ミュフ猫さんのレス (2007/02/05(Mon) 20:43)

toorisugari no Hiroさんの漸化式がめちゃめちゃヒントになりました．

まず，１番からn-1番までのカードと封筒をシャッフルした後，n番のカードと封筒を持ってきて，カードだけ，１⇔n ２⇔n ・・・ n-1⇔n というように入れ替える試行を考える．１番からn-1番までのカードと封筒をシャッフルする組み合わせは， a[n-1]通りで，各々のパターンに対してn-1通りの入れ替え方があり，明らかに，重複は起こらない．よって， (n-1)*a[n-1]通りは確保される．ここで，抜けがあるのは，例えば，１⇔n とカードを入れ替えた場合，１番の封筒にn番のカードは絶対に入らない．つまり，１番とn番のカードと封筒は，絶対に「タスキ掛け」にはならない．だから，n番とタスキ掛けになるパターンを加える．それは，明らかに， (n-1)*a[n-2]通りで，この中にも，重複は起こらない．よって結局，toorisugari no Hiroさんの漸化式が導出される．