kome さんの書込 (2007/02/05(Mon) 13:11)

はじめまして．

{1} 縮退していない３つのエネルギー準位があり，エネルギーの値は下から順に 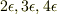とする． ・各エネルギー準位に上から順に１個，２個，３個の粒子が占め，各粒子が区別できる時，いくつのミクロ状態があるか． ・上記問題で，各粒子が区別できない時，いくつのミクロ状態があるか． ・全粒子数が６個で，全エネルギーが 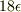のもとでは，各粒子が区別できる時と，区別できない時，それぞれいくつのミクロ状態があるか． ・前問で，各エネルギー準位が縮退度２の時の答えを求めよ．

{2} 単原子分子理想気体の分配関数zを 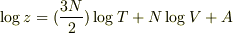とする時，内部エネルギーUを求めよ．また，定積比熱Cvを求めよ．

{3} f(x,y,z) = 0 で，dz = M(x,y)dx + N(x,y)dyとかける時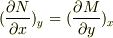， となることを示せ．

以上の３問が分かりません．学年は大学２年です．先生がきちんと説明してくれないので困っています．よろしくお願いします．

サボテン さんのレス (2007/02/05(Mon) 19:35)

1)・最初は個数の処理の問題です．エネルギー準位を上からA,B,Cとします．

Aに入れる入れ方は6通り，Bに入れる入れ方は5×4/(2×1)=10 6×10=60通り

・粒子が区別できないときは1通り ・Aの個数をx,Bの個数をy,Cの個数をzとすると， 4x+3y+2z=18 x+y+z=6 これより，2x+y=6 →(x,y,z)=(0,6,0)(1,4,1)(2,2,2)(3,0,3) 粒子が区別できる場合は 1+6_C_1・5_C_1+6_C_2・4_C_2+6_C_3 区別できない場合は4通り

縮退度が2の場合も同様に考えることができると思います．頑張って 計算してみて下さい．

2)β=1/(kT)とすると，U=-∂lnz/∂βより， z=-3N/2lnβ+(βに関係ない項)となり， U=3N/(2β)=3NkT/2 すみません・・・定積比熱の定義を忘れました．

3)f(x,y,z)=0より局所的にz=g(x,y)なる関数が存在します(厳密には陰関数定理 を使う必要がありますが・・・) dz=∂g/∂xdx+∂g/∂ydy より，∂g/∂x=M, ∂g/∂y=N よって∂^2g/∂x∂y=∂M/∂y=∂N/∂x

*最後の問題に関してはもっと綺麗な解き方があるかもしれません． 数学的にも厳密性を欠いてますし・・・．他の回答者の方の ご意見もご参考にして下さい．

kome さんのレス (2007/02/05(Mon) 21:38)

サボテンさん，ありがとうございます． 最後の問題は，サボテンさんの回答を見ながらもう一度やってみます． ちなみに，定積比熱Cvは 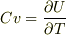だったと思います．