2004東工大前期の問題です
2004東工大前期の問題です
えり さんの書込 (2007/02/04(Sun) 23:08)
コンデンサーの電荷の問題なのですが,問題文と図は以下にあります.
私がわからなかったのは,t=t1直前になぜP2下面に2(ε0*L^2*V0)/Dが,t=t2直前になぜP1下面に2(ε0*L^2*V0)/Dが蓄えられているのだろうか,ということです. どうしてそのようになるのでしょうか,教えて下さい,お願いします.
Re: 2004東工大前期の問題です
zoro さんのレス (2007/02/05(Mon) 01:38)
問題の文字が小さすぎて,よく見えませんでした(泣).漸くPDFに気づき,問題が読めました(笑).
数式が複雑そうなので,取りあえず絵を描いてみます.で,わからない箇所に来たら書いてみてください.
なお,P1とP2の間隔x, P2とP3の間隔yとします.よって,D=x+y です.
また,題意によって,L >> D >= x,y の為に,電極周辺部の振る舞いは無視できるとする. <pre>-------------------------------------------------------------
■図1 [t <= 0] ■
yの領域では,電場Ey,電極面密度+σ0 とすれば;
Ey = σ0/ε0 V0 = Ey・y = Ey・D = σ0/ε0・D -----(1)
P2表面に生じる電荷: Q2]pre= σ0・L^2 = ε0・Ey・L^2 = ε0・V0・L^2/D
│ 電池B: 起電力V0 ┏━━━━┥┣━━━━━┓ ┃ │ ┃ ┏━━━━┻━━━┓ *接地へ ┃ P1 ┃ ┣━━━━━━━━┫ x=0 ┃ P2 ┃ ┗━━━━━━━━┛ +σ0 = +Q0 / L^2
y=D
-σ0 ┏━━━━━━━━┓ ┃ P3 ┃ ┗━━━━┳━━━┛ ┃ ━━┻━━接地 ━━━ ━
■図2 [0 < t < t1 =(D/v)] ■
│ 電池B: 起電力V0 ┏━━━━┥┣━━━━━┓ ┃ │ ┃ ┏━━━━┻━━━┓ *接地へ ┃ P1 ┃ ┗━━━━━━━━┛ +σ1 = +Q1 / L^2 ↓x -σ1 ┏━━━━━━━━┓ ┃ P2 ┃ -σ1 +σ2 = +σ0 (分離時に,P1とP2の境界に電荷は無い) ┗━━━━━━━━┛ +σ2 = +Q2 / L^2
↓y=D-x
-σ2 ┏━━━━━━━━┓ ┃ P3 ┃ ┗━━━━┳━━━┛ ┃ ━━┻━━接地 ━━━ ━ - - - - - - - - - - - - - - - - - - - - - - - - - - -
この領域の味噌は,図1で接触した部分が,外力によってP1とP2の接触面が無理矢理に剥がされる所だと思います. このP1とP2の接触面では,その寸前まで一体の金属として振る舞っていますから, 定常状態として電流の流れは無く,当然電荷の発生も無い訳です.
従って「t=0」の時点で,切り離されたP2の下面に生じていた電荷,+σ0・L^2がP2に真電荷として取り残される訳です. この電荷の為に,P2の上下に発生する面電荷は絶対値が同じになれないのです.
#こんな状況の問題は初めて見ました.上の解釈がすぐに出来ず,紅茶を1杯入れ直しました. こんな問題を考案した出題者さんには脱帽です. #でも,本番で出てくると,「紅茶...」の余裕が無いので慌てそうです. #そんな時は,「紅茶...」の替わりに「深呼吸...」で落ち着いて, 原点にもどって見直しましょうね.
xの領域では,電場Ex,電極面密度σ1 とすれば;
Ex = σ1/ε0 V1 - V2 = Ex・x =σ1/ε0・x --------(2)
yの領域では,電場Ey,電極面密度σ2 とすれば;
Ey = σ2/ε0 V2 - V3 = Ey・y = =σ2/ε0・y -------(3)
P2の全(真)電荷Q2に付いて -Q1 + Q2 = (-σ1 +σ2)・L^2 = Q2]pre = σ0・L^2 = +Q0 ------(4)
全電位について V0 = (V1 - V2) + (V2 -V3) -------(5a)
題意より V_D = V2 - V3 -------------------(5b) 故に, V1 - V2 = V0 - V_D --------------(5c) </pre>
以上の関係式を,連立して解けば良いですね.
そこで「t=t1直前になぜP2下面に2(ε0*L^2*V0)/D」ですが,図2のP2のように,P2下面には,「+σ2・L^2(ただしx=D)」が出ますね.
きっと連立式を解けば,上の電荷もうまく与えられると思います.
せっかく解いたら,どうして「2」という係数が出てくるかを考えると面白いですね.ひょっとすると,スマートな別解に出会えるかも知れません.
Re: 2004東工大前期の問題です
えり さんのレス (2007/02/05(Mon) 23:41)
まだ式を連立していませんが,まず最初にお礼を・・・ ご丁寧な図まで描いていただき,ありがとうございました.
最初にどうして「2」がつくのかと考えたとき,電極板の厚さが関係しているのかなと思ったのですが,違うんですね(汗)
またわからなくなったら質問することになると思いますが,そのときは宜しくお願いします.
Re: 2004東工大前期の問題です
zoro さんのレス (2007/02/17(Sat) 00:50)
少し時間が空いてしまいましたが,時間が取れたので,電極P2が最上位置(x=0)から最下位置(x=D)まで動く時の計算をしてみます.
この問題は,基本に従って解こうとすれば素直に解けるようですが,幾つものトラップがあるので,冷静に一歩一歩進む必要がありそうです.その代り,幾つもの類題ができるほど,巧い問題のように思えます.
そこで,すこし丁寧に自分の場合の計算と,それに関係する考え方を書いて見ます.
====
図1の式(1)で求めた電荷;
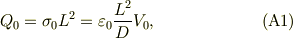
が,P2がP1から分離した時に,P2に置き去りにされる為に,それがP2の真電荷となることです.
#高校の物理では,平衡板コンデンサをどう教えているか知りません.
#私は,金属表面近傍では,そこから出てくる電場は,
その法線方向 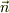 だけで,その強度は金属の表面電荷密度に比例し,
ε0に反比例すると定義してしまって言いと思います.
だけで,その強度は金属の表面電荷密度に比例し,
ε0に反比例すると定義してしまって言いと思います.

#無限平面とか,無限同心円筒とか,球殻といった対称性の高い場合がいえます. その極端な例として,クーロンの法則を考えます:
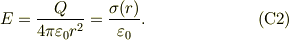
ですよね.なにか困ったら,式(C1,2)を思い出すと良いかもね.
図1→図2のハイライトは,外力によってP2がP1から剥される時に,そこの間には電荷分布が無いことですね.
図2の表面電荷について,題意よりP2の電位が 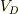 と書かれる事に注意すれば,
と書かれる事に注意すれば,
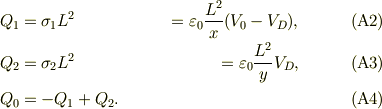
すでに式(A2)が問い(a)の答えです.
#ここで注意するべきは,x=0で発散しそうですが, 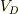 が解かれていない事ですね.
が解かれていない事ですね.
あとは,式(A1~A4)から, 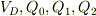 を,距離と印加電圧で表せばよい.式(A4)に電荷の電位表現を代入すれば;
を,距離と印加電圧で表せばよい.式(A4)に電荷の電位表現を代入すれば;
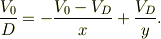
整理して
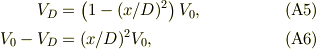
となる.これらから,
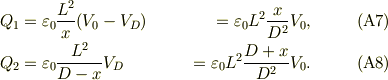
#オリジナルのご質問「t=t1直前になぜP2下面に2(ε0*L^2*V0)/D」は,式(A8)で,「x → D」とすればいいですね.面白いのは,P2の上面にはこの電荷半分で逆符号の電荷となることです.
さらに式(A1)を用いて;
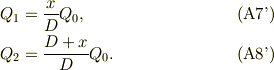
#この式を考えるのに,P2に真電荷の無い場合を考えると, 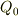 であることが判ります.丁度,普通の直列接続と同じです.そこで,これを括りだすと,
であることが判ります.丁度,普通の直列接続と同じです.そこで,これを括りだすと,
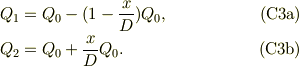
Q_{0}に対する補正項は,P2に真電荷を与え,P1,P2のポテンシャルをゼロにした場合に,静電誘導で生じる電荷項です(式の打ち込みは未完).
要は,二つの状態:
●P2に真電荷なして通常の直列にして電位を印加した場合の解 ●P2に真電荷だけ注入して,両端をショートした場合の解
の足し合わせ(線形和)で与える事ができる.
気分転換の為に,次のページに続けます.
Re: 2004東工大前期の問題です
zoro さんのレス (2007/02/17(Sat) 10:32)
■図3 P2に真電荷,P1とP3を接地 ■ <pre>
起電力=0 │ 電池B: ┏━━━━┥┣━━━━━┓ ┃ │ ┃ ┏━━━━┻━━━┓ *接地へ ┃ P1 ┃ ┗━━━━━━━━┛ -σ_T ↑x +σ_T = +Q_T / L^2 ┏━━━━━━━━┓ ┃ P2 ┃ +σ_T +σ_B = +σ0 (真電荷),電位差:V_D ┗━━━━━━━━┛ +σ_B = +Q_B / L^2
↓y=D-x
-σ_B ┏━━━━━━━━┓ ┃ P3 ┃ ┗━━━━┳━━━┛ ┃ ━━┻━━接地 ━━━ ━
ここで,(起電力=0の電池)=(単純な短絡・電線),に注意のこと.
起電力=0 │ 電池B: ┏━━━━┥┣━━━━━┓ ┃ │ ┃ *接地へ
↑(等価)↓
電線で短絡 ┏━━━━━━━━━━━┓ ┃ ┃ *接地へ </pre>
やや見慣れない絵になっていますが,よく見れば,P2からP1とP3に並列コンデンサで地球に接続している状態ですね.それぞれのポテンシャルの電位積分が等しいから,
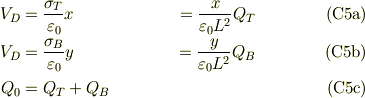
これを解けば,
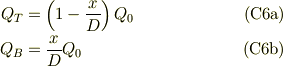
前の検討式(C3a,b)は,
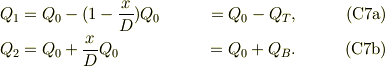
と二つの状態の重ね合わせであることが判ります.このことを確認する為に,図2を図上で分解して,重ね合わせを表示してみましょう:
■図4 図2の状態を図上で重ねあわしてみる ■ <pre>(a) 外部電位差V0印加,P2は無電荷(b) P1とP3は接地,P2に真電荷Q0 (c) (a)と(b)とを加えると図2!
#(起電力がゼロの電池)=(電線) 起電力=V0 │ 電池B: 起電力=0 │ 電池B: 起電力=V0 + 0 = V0 ┏━━━━┥┣━━━┓ ┏━━━━┥┣━━━┓ ┃ │ ┃ ┃ │ ┃ ┏━━┻━━━┓ *接地へ ┏━━┻━━━┓ *接地へ ┃ P1 ┃ ┃ P1 ┃ ┗━━━━━━┛ ┗━━━━━━┛ +σ0 -σ_T (+σ0) +(-σ_T) = +σ1 ↓x ↑x -σ0 +σ_T = +Q_T / L^2 (-σ0) +(+σ_T) = -σ1 ┏━━━━━━┓ ┏━━━━━━┓ ┃P2:電位V'2 ┃ 真電荷なし; ┃P2:電位V''2┃ +σ_T +σ_B = +σ0 (0) +(+σ0) = +σ0 ┗━━━━━━┛ ┗━━━━━━┛ +σ0 +σ_B = +Q_B / L^2 (+σ0) +(+σ_B) = +σ2
↓y=D-x
-σ0 -σ_B (-σ0) +(-σ_T) = -σ2 ┏━━━━━━┓ ┏━━━━━━┓ ┃ P3 ┃ ┃ P3 ┃ ┗━━━┳━━┛ ┗━━━┳━━┛ ┃ ┃ ━━┻━━*接地 ━━┻━━*接地 /// /// </pre>
問題対象である図2の状態とは,上記の左図(a)に,真電荷Q0を注入して出来た右図(b)の電荷分布を加え合わせたと考える事が出来る.それが,式(C7a,b)の意味だと思います.電磁場のが,線形の微分方程式である為です.
念の為に其々のP2のP3に対する電位差, V'2とV''2 を求めておきますと;
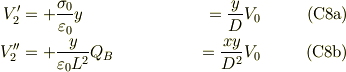
これらを片々加えて,式(A5)と比較すると,なんと,一致しますね.
#遡ると少なくともクーロンの法則がなりたっているからさ.
===
以上で解釈を終わります.
==== 《この問題をに触れていた時の感想》
解釈すればするほど,ある種の違和感が強くなって来ました.ここまで,複雑な問題を解ける高校生さんがどれほどいるのでしょうか? スラスラと回答できるなら,大学の電磁気をほぼマスタしている可能性が高いと思います.
ここまでの力量を入試の問題で要求するのは,やはり行き過ぎであるようにも思います.勿論,私自身が高校生のころ,こんな問題が出されたらパニックになったと思います.
他方,個人的には,この出題者さんの発想には敬意を払うものであります.願わくば,学生さんに噛み砕いた講義をして,罪滅ぼしをしてもらいたいものです.
でもしかし,「冷静に,ステップを踏めば」解ける問題であるのも事実だろうと思います.慌てずにゲーム感覚でアタックしたいですね.
一応,完結.
Re: 2004東工大前期の問題です
えり さんのレス (2007/02/17(Sat) 14:31)
再度,詳しい解説どうもありがとうございました. 一応自分でもう一度問題と解説を照らし合わせて紙に起こして考えました. なぜt=t1のときにP2の下面の電荷に2がつくのかわかりました!!どうもありがとうございました. そのときにいくつか確認したいこととわからないところが(理解力がない私のせいです)ありましたので質問させていただきます.
「図1→図2のハイライトは,外力によってP2がP1から剥される時に,そこの間には電荷分布が無いことですね.」 →初期状態ではP2下面表面にのみ電荷がたまっていると考えてよいからですよね?
また,A2式では,P2からみた電位,A3式ではP3からみた電位としているのですよね?
「#ここで注意するべきは,x=0で発散しそうですが,?Dが解かれていない事ですね」 →ということは?Dがこの問題の未知数であって,これを求めないと,P2下面の電荷がわからないのですね.
「面白いのは,P2の上面にはこの電荷半分で逆符号の電荷となることです.」 →P1の下面と電荷が保存しているからですよね?
それと,図3のようにP1が接地されていると見ることができるのはなぜなのでしょうか・・・電源電圧は無視できるのですか?図3のように見れるとすれば,P1の下面の電荷面密度が負になるのもわかるのですが,図1や図2のように見ると,P1が接地されているのにも関わらず接地点との電位差が?0ということがよくわかりません(>_<)それとも図1,2と図3の間には何か着眼点の違いがあるのでしょうか・・・
なんかいつまでもすみません..
Re: 2004東工大前期の問題です
zoro さんのレス (2007/02/17(Sat) 15:27)
えりさん,
>>「図1→図2のハイライトは,外力によってP2がP1から剥される時に,そこの間には電荷分布が無いことですね.」 >→初期状態ではP2下面表面にのみ電荷がたまっていると考えてよいからですよね?
そう思います.
>また,A2式では,P2からみた電位,A3式ではP3からみた電位としているのですよね?
我々は,絶対電位を決められないと思って良いでしょう.今の場合,P3と電地のマイナス極側が接地されています.理想的には,接地した電位は変動しないと考えて,一定の電位にあるとします.考え易くする為に,接地の電位をゼロとしてしまうのだと思います.
接地されるという場合,重要なのは接地側に,いくらでも電荷が出入りできる事だと考えています.でも,それは「接地の電位=0」ということに直結していないとおもっています.
また,電場の積分により電位差が定義できるだけなので,明示的に電位差とかいてみました.
この解説は,答えを出す事よりも,考え方に拘りました.昨年,えりさんがCOさんに微積分を使った物理の教科書を教えていただいて,その勉強をしているだろうから,大学新入生の方に説明するつもりで書きました(笑).
>>「#ここで注意するべきは,x=0で発散しそうですが,?Dが解かれていない事ですね」 >→ということは?Dがこの問題の未知数であって,これを求めないと,P2下面の電荷がわからないのですね.
さうだと思います.私は,常に図を先に書き(実際は頭の中だけが多いですが,この場合は,常用でないPCの練習の為に,直接PCに書いた),そえから式を書き流して行き,それから連立方程式を見当します.今回のコメントは,ほとんど実際の流れに即しています.
でも,慌てると,VDを解かないで式の中に置いておけないように思います.そのような意味で,意地悪トラップと思いますよ.
>>「面白いのは,P2の上面にはこの電荷半分で逆符号の電荷となることです.」 >→P1の下面と電荷が保存しているからですよね?
金属版の平衡コンデンサでは,一方の電極から出た電場は他方の電極に入り込む為に,電荷がバランスしていると考えられます.これは,無限平面により電極に平行な電場成分が作れないのが本質的と思います.
>それと,図3のようにP1が接地されていると見ることができるのはなぜなのでしょうか・・・電源電圧は無視できるのですか?図3のように見れるとすれば, P1の下面の電荷面密度が負になるのもわかるのですが,図1や図2のように見ると,P1が接地されているのにも関わらず接地点との電位差が?0ということがよくわかりません(>_<)それとも図1,2と図3の間には何か着眼点の違いがあるのでしょうか・・・
図3だけだと,考え難いと思って,図4を書き出したものの,作図に手こずっています.確かに,図3は考え難いかも知れませんね.私も巧く説明できないところもあります.問題はすでに解かれたと思うので,とりあえずは無視しておいてください.
図4へのアタックは,もうすこし続けてみます.
Re: 2004東工大前期の問題です
えり さんのレス (2007/02/17(Sat) 16:36)
図4へのアタックは,もうすこし続けてみます. →ありがとうございます.
「接地されるという場合,重要なのは接地側に,いくらでも電荷が出入りできる事だと考えています.でも,それは「接地の電位=0」ということに直結していないとおもっています.」 →例の微分を使った教科書では,「接地点を電位の基準とすることがアースの意味」とあるのですが,それはどのように考えればいいでしょうか(実はいつも私は接地が入ってくると途端にわからなくなってしまうのです・・・).
それと,再度図1,2について質問させてください.P1は接地されていますが,そうすると等電位になって図3,4のように電位差0になるはずだと思うのですが,そのようにならないのはなぜでしょうか(あ,これをとりあえず無視しておけばいいってことでしょうか)..
Re: 2004東工大前期の問題です
zoro さんのレス (2007/02/17(Sat) 18:24)
>→例の微分を使った教科書では,「接地点を電位の基準とすることがアースの意味」とあるのですが,それはどのように考えればいいでしょうか(実はいつも私は接地が入ってくると途端にわからなくなってしまうのです・・・).
これに付いては,図4が片付いたら,再度論議しましょう.ここも急所ですよね.私は,自分の入試のときには「接地問題」は捨てていました(苦笑).
>それと,再度図1,2について質問させてください.P1は接地されていますが,そうすると等電位になって図3,4のように電位差0になるはずだと思うのですが,そのようにならないのはなぜでしょうか(あ,これをとりあえず無視しておけばいいってことでしょうか)..
図を書くときにサボりましたが,図1,2で,「電位差:V0 ----*接地へ」と書いたのは,《電位差:V0》が直流電圧電源の積もりでした.後で書き直します.pdf資料に立派な図がついていたと思うので,そちらでイメージを確認してください.たしか電流計まで書き込んであったようでしたね.
Re: 2004東工大前期の問題です
えり さんのレス (2007/02/17(Sat) 20:05)
「これに付いては,図4が片付いたら,再度論議しましょう.ここも急所ですよね.私は,自分の入試のときには「接地問題」は捨てていました(苦笑).」 →論議していただけるんですか?どうもありがとうございますm(__)m
「これらを片々加えて,式(A5)と比較するとなんと,一致しますね. #遡ると少なくともクーロンの法則がなりたっているからさ.」 →うーむ,なんとなくわかりました..
ちょっと体調があまりよくないので今日は休ませてください…連日入試で疲れがきたみたいです..すみません.
Re: 2004東工大前期の問題です
zoro さんのレス (2007/02/17(Sat) 20:18)
>→うーむ,なんとなくわかりました..
というアバウトな感覚も大切にしてね.真面目ばっかりだと飛躍できないような ....
>ちょっと体調があまりよくないので今日は休ませてください…連日入試で疲れがきたみたいです..すみません.
週間朝日に,鎌田 實(かまた みのる)さんという医師で,長野県の医療活動(農村医療,ターミナル・ケア)や中東での医療ボランティアで実績のある方のコラムに「がんばらないけど あきらめない」があります.
この1年,頑張ってきた実績に信頼を寄せて,無理せずに,じっくり行きましょう.体力の回復は大事ですね.
Re: 2004東工大前期の問題です
zoro さんのレス (2007/02/18(Sun) 19:10)
<pre>■ ■ ■ 接地について ■ ■ ■ </pre>>→例の微分を使った教科書では,「接地点を電位の基準とすることがアースの意味」とあるのですが,それはどのように考えればいいでしょうか(実はいつも私は接地が入ってくると途端にわからなくなってしまうのです・・・).
■ 物理用語としての接地 ■
接地というのも,物理学でしばしば用いられる「理想化」の一法だと思います.力学で言う「質点」,理想的な「バネ」,「摩擦力のない完全平坦な平面」静電気での「点電荷」,「完全流体」,「完全気体」など,問題解決の強力な手法の一つと思います.
私の偏見と独断かも知れませんが,工学と理学とに差があるとすれば,工学では「理想化を抜きにして,課題にすこしでも正確な解をだすこと」が目的で,理学では「理想化によって,課題に含まれる大筋の機構を浮き出させること」が目的であると思います.
#最近は,少し様子が変わりつつありますね. # ##電磁気の教科書でも,工学部の方が, 善い意味で,とてもアヴァンギャルド(前衛的)なテキストを発表されたり, ##生命科学を中心に,これまでの枠組みを壊すような仕組み; 工学部,理学部 → 生命理工学部のような新設がでたり, ##国を越えた大学間の連携が始まったり, # #などと,新しい波が来てるのかもしれません. #若人には,チャンス到来とも感じます.
この問題の中で出て来る「他の理想化」の関連項目を書き出しておきましょう; ・電池の「内部抵抗」は無視できるものとする. 《だから,状態が変わるにつれて電荷の出入り必要になると, 幾らでも,その電荷を接地側に渡すことが出来る.》 ・Lは "P1-P3"間の距離に比べて十分に大きく, 《電極間の電場は,電極面に垂直な成分と理想化できる》とする.
#ここで,《 ...》の部分は,私の注釈です.
このページでは,以下に,「理想化された接地の働き」を再考し,この出題と比較して見たいと思います.
● 接地の電位
最初に注意させて戴きたいのは,接地が有効なのは「静電場現象」であって,「電磁波現象」や「静磁場現象」とは関係しないことですね.特に「静」を忘れて「電場現象」に拡大解釈して困ることが往々にあります.
今回でも,P2を動かすことから「動電場現象」の可能性がありますが,出題者さんは,『P2の動く速さvは,十分にゆっくりであり,その速さで電荷が動くことにより発生する磁界などは無視できるほど小さい.』としっかり釘を刺されていますね.
さて,電位は絶対的なものではありません.二点間の電位の差が電場と直接に関連を持つことが大切です(この点は,大学でじっくり勉強してください).ですから,考察するときに,適当な基準点を決め,その地点での電位との差で表示するだけでいいわけです.この基準点での電位の変動が十分に少なければ,それをZeroに決めることが出来るので,いちいち差分を取らないで済むので楽ですね.そこで接地の電位をZeroとすることが多いと思います.
今回の問題では「P3」や「電池の負極」が接地されていますね.でも式を立てるときは,「接地から見たP1の相対電位」を「P1の電位」と略称している事を意識の片隅において置くといいでしょう.
● 接地のイメージと役割
私は,「接地」と聴くと,「直径20mほどの適度に湿った土の塊」をイメージします.要は,表面積が巨大なある程度,電気伝導ができる物体なら,少しぐらいの電荷の出入りによって,顕著な電場が発生しないため,「考察したい系」に静電場を通して作用しないと考えられるからです.
では,接地すると何が変わるのでしょうか? それは「考える系」が;
「外部と静電的に結合することを防いでくれる」
言い換えると,
<b>「外部に接する電極部に電荷の発生をさせない」</b>
事だとおもいます.と,言われても,「なんの事?」だろうと思いますので,この問題を例にして考えて行きましょう.
- 具体的に,図4を基にして説明します.この図で;
- <b>P1の上面,P3の下面には電荷が存在しません </b>
この為に,これらの系を簡単に計算できた訳です.その理由は,幾らでも「不必要な電荷を引き受けてくれる"万能の神",<b>接地</b>さん」のお蔭なのですね.
#もし,逆に,「P1の上面,P3の下面には電荷が存在する」と, 其々の電極と外部との間の「電場の積分」が必要となってしまい, 簡単に計算が出来なくなるからです. #ようは,細かな点を細かく計算して,時間を浪費し,見通しが悪いより, 明確に単純化して,大雑把な理解をしようとする「思想」だと思います. #勿論,精密化が意味を持ち始めれば,次のステージに進むだけだと思います.
そう考えて,もう一度,図4(a) を見れば,2つのコンデンサ;「P1下部とP2上部」,「P2下部と P3上部」が直列に接続しているのが判りますね.
同様に,図4(b)を見ると,P2が一つの電極で,「P2上部とP1下部」,「P2下部と P3上部」とが並列に接地に接続しているように見えますね.ここで大切なのは「P2」の真電荷に対応する電荷分布を作る際に,「電池の内部抵抗を無視できる」という理想化が大切です.
==== 一応,説明は完了.
苦手な箇所が在れば,具体的な問題と合わせて書いてください.判る範囲で検討します.判らなければ,ご免なさい.
====ふろく「吟味」
この解説を書いていたら「吟味」と言う言葉を思い出しました.1年生の今頃は,電磁気に一辺倒でしたが,ほとんど演習問題を解きませんでした.
が自己流で勉強していた電磁気学の本は「例題がしっかり説明されていた」ので,例題にぶつかると,これを軽めに読んで,別途自分で解きました.このとき自分の回答と再度,その本の例題を突き合せる時に「吟味」すると言っていました.少なくとも,今の自分が解説を参考書なしで書けるのは,当時の吟味の御蔭だろうと思います.
Re: 2004東工大前期の問題です
えり さんのレス (2007/02/19(Mon) 23:29)
体調はお蔭様で回復しつつあります. 接地の大枠は掴めました.本当にどうもありがとうございました.
「図4(b)を見ると,P2が一つの電極で,「P2上部とP1下部」,「P2下部と P3上部」とが並列に接地に接続しているように見えますね.」 →ここら辺はあまりイメージがわいてこないのですが,要は(a)も(b)もP1,P3が結局は接地に接続されているということが大切なのですよね.
「さて,電位は絶対的なものではありません.二点間の電位の差が電場と直接に関連を持つことが大切です(この点は,大学でじっくり勉強してください).ですから,考察するときに,適当な基準点を決め,その地点での電位との差で表示するだけでいいわけです.この基準点での電位の変動が十分に少なければ,それをZeroに決めることが出来るので,いちいち差分を取らないで済むので楽ですね.そこで接地の電位をZeroとすることが多いと思います.」 →なるほど,そうなんだーという感じで勉強になりました.
今回のスレッドは(も!)特に自分自身すごくためになるものばかりでした.いつも興味深いコメントをしていただき,どうもありがとうございます.これからもどうぞよろしくお願いします.(いつか私にも物理について熱く語れる日が来るといいなぁ・・・)
Re: 2004東工大前期の問題です
zoro さんのレス (2007/02/20(Tue) 00:39)
問題に出ている「電池」でも,使い続けるより,すこし休ませながら使うと「回復」しますよね.電池は化学反応ですが,主な反応に平行して,多数の副次的な反応があり,これが「少しの急用で,機能が復元する」といった話を聴いた気がします.
まして,複雑な生化学反応と精神活動をするヒトには,「休む」事は大事だとおもいますよ.
なお,今気がつきましたが,静電容量を使っての説明の方が,自然だったかと思うようになりました.まあ,大学で電磁気を始めたら,「あっそうだったのか」になるでしょう.回りくどい説明,ご免なさい.
>→ここら辺はあまりイメージがわいてこないのですが,要は(a)も(b)もP1,P3が結局は接地に接続されているということが大切なのですよね.
いわゆる静電容量(コンデンサ)の記号で図を書いてみます,後で.
>接地の大枠は掴めました.
いい感じですね.もう少しすれば「吸収」しきると思います.
>(いつか私にも物理について熱く語れる日が来るといいなぁ・・・)
そう思えば,いつか知らぬ間に,そうなるのでしょう.どうして言い切れるかというと,スレッドの冒頭で,
>私がわからなかったのは,t=t1直前になぜP2下面に2(ε0*L^2*V0)/Dが,t=t2直前になぜP1下面に2(ε0*L^2*V0)/Dが蓄えられているのだろうか,ということです.
多くの方が,塾の問題を見てファクタ「2」を目にされたと思います.しかし実際に,「その原因がなぜなのか」に疑問を集中できた事が大切であると感じます.
やはり,「問題が解ける」のは受験を突破する必要な技量でしょうが,「どうしてなのか」という感覚はそれ以上に貴重だと思えるからです.勿論,これらを両輪としてベストを尽くしてください,リラックスも入れてね.
Re: 2004東工大前期の問題です
zoro さんのレス (2007/02/20(Tue) 02:22)
● 図5 図4(a,b)を回路記号で表示してみる
- 外部電位差V0印加,P2は無電荷
<pre> 電位:V0 ┏━━━━━━━━━━━━┓ ┃┃ P1 ┃ ┃ ━┻━ +Q0 P1下部 ┃ x↓ 起電力V0┃ ━┳━ -Q0 P2上部 ─┸─ P2┃ ┳ ━┻━ +Q0 P2下部電池B┃ y↓ ┃ ━┳━ -Q0 P3上部 ┃ P3┃┃ ┗━━━━━┳━━━━━━┛ ━┻━ 接地:電位0とする. //// </pre>
(b) P1とP3は接地,P2に真電荷Q0 <pre> SW:仮想的に電池Cに接続に,SWを切っても,同じこと. ━┳━ ┏━━━━━━━┳━━━━━━━━━━━┓ ┃┃┃ 起電力V''2┃┃ ┃ ─┸─ ━┻━ +Q_B P2下部━┻━ +Q_T P2上部 ┳y↓ x↓ Q_T + Q_B = Q0
電池C┃━┳━ -Q_B P3上部 ━┳━ -Q_T P1下部
┃┃┃ ┗━━━┳━━━━┻━━━━━━━━━━━┛ ━┻━ 接地:電位0とする. ////
【注記】(b)のキャプションが図4で間違っていたので修正しました.
</pre>
Re: 2004東工大前期の問題です
えり さんのレス (2007/02/20(Tue) 23:03)
はい,適度に頑張ります(^^)詳しい図もどうもありがとうございました. あ,そういえば重心運動の問題を出題した大学には無事受かることができました(ほっ)
それから,話が少しずれるんですが,起電力が―l|―だとしたら,今プラスの端子が右にありますが,電流が左向きに流れることはあるのでしょうか?
Re: 2004東工大前期の問題です
zoro さんのレス (2007/02/20(Tue) 23:15)
>あ,そういえば重心運動の問題を出題した大学には無事受かることができました(ほっ)
それを聴いて,私も(ほっ).リラックスすると免疫力も向上するとか.
>起電力が―l|―だとしたら,今プラスの端子が右にありますが,電流が左向きに流れることはあるのでしょうか?
他の起電力源がなければ,電池が逆向きの電流を流すことはないと思います.
確かに一つの回路に複数の電源をつけることはあります.でも電源に逆流を起こすのは大変危険だと思います.
Re: 2004東工大前期の問題です
えり さんのレス (2007/02/20(Tue) 23:30)
たとえば,ダイオードが電流回路に(電池の自然な流れの向きを妨げるような向きに)接続されている場合も逆流はしないのでしょうか・・・(予備校のノートでそのような向きに電流が流れている回路があるのですが・・・)
「この電池の記号は,どうやって書いたか教えて頂けますか?」 →”―”は全角ハイフン,”l|”は左が半角小文字のエル,右が半角縦線です(^▽^)
Re: 2004東工大前期の問題です
zoro さんのレス (2007/02/20(Tue) 23:44)
>たとえば,ダイオードが電流回路に(電池の自然な流れの向きを妨げるような向きに)接続されている場合も逆流はしないのでしょうか・・・(予備校のノートでそのような向きに電流が流れている回路があるのですが・・・)
ダイオードは完全に逆電流がゼロにはなりません.ツェナー効果といい,ある逆電位を越えると,急に逆電流が増加することがあります.また,順方向も素子の物性を反映した電圧降下を過ぎてから電流は急増します.
こんな細かいことも物理のノートに書かれているとは ....
>「この電池の記号は,どうやって書いたか教えて頂けますか?」 →”―”は全角ハイフン,”l|”は左が半角小文字のエル,右が半角縦線です(^▽^)
なるほ〜〜〜ど,気が付きませんでした,有難うございました.
Re: 2004東工大前期の問題です
えり さんのレス (2007/02/20(Tue) 23:57)
「ダイオードは完全に逆電流がゼロにはなりません.ツェナー効果といい,ある逆電位を越えると,急に逆電流が増加することがあります.また,順方向も素子の物性を反映した電圧降下を過ぎてから電流は急増します.」 →難解で私にはまだよくわかりませんが,逆流はしないとみていいのですよね?
「こんな細かいことも物理のノートに書かれているとは ....」 →もしかしたら私がノートを写し間違えてるだけかも・・・涙
「なるほ〜〜〜ど,気が付きませんでした,有難うございました. 」 →大学生になったら,私もTeX数式を使えるように練習しなくちゃ!!
どうもありがとうございました(^^)
Re: 2004東工大前期の問題です
zoro さんのレス (2007/02/21(Wed) 00:19)
>→難解で私にはまだよくわかりませんが,逆流はしないとみていいのですよね?
物性は苦手なので,用語ぐらいしか知らず,噛み砕いて説明できません.きっと,入試にまでは出ないように思いますが ....
#基本は,文科省の検閲をうけた教科書にどう書かれているかによると思います.
>→大学生になったら,私もTeX数式を使えるように練習しなくちゃ!!
は,超お勧めだと思います.「なんでも気が付いたら,即ノート」にして置けますし.
あと少しの辛抱ですが,肩の力を抜いて,じっくりトライしてください.
Re: 2004東工大前期の問題です
MXK さんのレス (2007/02/21(Wed) 00:36)
> それから,話が少しずれるんですが,起電力が―l|―だとしたら,今プラスの端子が右にありますが,電流が左向きに流れることはあるのでしょうか?
ありえます.
定電圧源は「端子間の間の電位差を一定に保つために,どのような 電流も流せる」というのがお約束です.
現実の電源は必ずしもそのようには動きませんが,定電圧源の記号が, 特にコメントなしに現れた場合は,そのように解釈して問題はないと 思います.
Re: 2004東工大前期の問題です
zoro さんのレス (2007/02/21(Wed) 01:45)
MXKさん,
>定電圧源は「端子間の間の電位差を一定に保つために,どのような >電流も流せる」というのがお約束です.
これは,高校の物理の教科書でも,このように定義されていますか?
また,大学の入試に,電源に逆方向の電流を明示的に流すような問題が想定されるでしょうか?
というのも,自分の頭では,回路上,逆方向の電流が流れるとすると,
・他の電源とか発電素子を逆向きに入れて,基の電源電圧を上回る場合. ・インダクタンス成分の逆起電力がとても大きく,電源電圧を凌ぐ場合. ・今まで設定していた電源電圧を,急に小さな値に変化させた場合(?)
ぐらいしか思い浮かびません.
もし入試にありえる状況がございましたら,お教えくださいませんか? 私も,勉強させて戴きたいと存じます.
Re: 2004東工大前期の問題です
MXK さんのレス (2007/02/21(Wed) 10:31)
回路内に電源が複数ある場合,逆電流の可能性がありますね.
典型的な例としては,直流電位差計があります. 電池の起電力を測定する装置で,最終的には電流が流れない 状態に調整してゆきますが,その過程では正負の電流を 流すことになります.
普通の電池(マンガン電池など)は大きい逆電流を長時間流し続けると, 発熱して危険な状態になります. ハイブリッド車の電池などは,逆電流(つまり充電電流)がバンバン流れて いるはずです.
Re: 2004東工大前期の問題です
zoro さんのレス (2007/02/21(Wed) 12:00)
MXKさん,ご解説感謝いたします.
これから推測できるのは,逆電流があるとすしても,特殊な条件下の出来事と思われます.従って,入試での心配は低かろうとおもいます.
さて,コンデンサの一部が動くと言う,アクロバティックな問題を観察してきたので,MXKさんが示された逆電流の問題に関して,さらに私の目で感じたことを補填したいと思います.
- 回路内に電源が複数ある場合
USBが普及する前のPCでの周辺機器は,PCからの+5V電源だけでした.どうしても高い電圧が欲しい時には,一度,交流に変換して電圧を上げて,それを直流に戻した(DC-DCコンバータ)のだろうと思います.USBは,PCから約3V(うろ覚え)の電圧しか来ないので,驚いた事があります.
普通の計測回路でも,電源には,ロジックIC用の+5V, アナログ回路用の+/-12Vとかの複数電源は日常的に使われます.でも定常的な逆電流が電源に流れる回路設計は,火災事故の危険性が高く,そのような設計は許されません.
- 直流電位差計
電池は,広い意味での電気化学の領域です.ここでは,電位差の基準を決める「参照電極」とか「基準電極」と呼ばれる電極からの差として考察する電極の電位を決めます.丁度,今回説明した,「接地」の役割と似ています.
電池の場合,外部負荷を取っていない(外部に電流を供給していない)時の電位を「自然電位」と呼び,重要な指標です.これを出すには,ポテンショスタットという回路で,上にご説明されたように調整します.現在,60歳代後半の先輩のお話では,人間が電流計を見ながら電位を調節したので,人間ポテンショスタットといって辛い実験だったという話です.
- 普通の電池(マンガン電池など)は大きい逆電流を長時間流し続けると,発熱して危険
私は,中学生の時,セレン整流器というドデカイ物をもらい,実際に電池を充電しようとしました.途中で怖くなって直ぐやめました.電池が少し暖かくなっていて驚きましたが ....
- ハイブリッド車の電池
知り合いがトヨタ・プリウスに乗っているので,時々同乗していて,運転モードの表示を見ていると,まさに充放電の繰り返しですね.「燃料電池の恐怖」もそうですが「ハイブリッドでの充放電数」も結構シビアな問題なのでしょうね.
でも,これを物理の問題として論じられる危険性はとても低い,はっきり予測すればゼロといいても過言ではないと思います.
==== 以上,「逆電流」の雑学でした.
Re: 2004東工大前期の問題です
MXK さんのレス (2007/02/22(Thu) 19:34)
>これから推測できるのは,逆電流があるとすしても,特殊な条件下の出来事と思われます.従って,入試での心配は低かろうとおもいます.
そうではなくて,人が後ろ向きに歩ける程度には一般的状況だと申し上げたつもりです.電位差計は高校物理でも扱われる素材だと思います.
Re: 2004東工大前期の問題です
zoro さんのレス (2007/02/22(Thu) 20:37)
>人が後ろ向きに歩ける程度には一般的状況だと申し上げたつもりです.
宜しければ,具体的にお教え下さいませんか.とくに,高校の物理の範疇でご説明くださると幸いです.ここに直接質問を書き込まなくても,多くの高校生さん達,とくに受験の最中の方々が多くご覧になっていると思いますので,「判り易いご説明」をお願いします.
関連して申し上げると,私は現在の高校教育での物理を全く存じません.もし間違えを申し上げているとお気づきの場合,ドシドシとご指摘いただければ幸いです.
恐らく,ご自分の研究室に所属されている学生さん達をご指導されている時の状況とは,著しい乖離があると推察いたします.是非とも,低レベルの世界の住人を相手にご説明なさっている,という点にご留意下されると幸甚でございます.ご発言の3〜10倍程度詳しくないと,私には到底理解できそうもありません.
■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■ 「起電力・逆起電力の混成系」の問題が,入試で出題される可能性については, 明確な根拠に基づく発言では在りませんでした.この問題に関する私の推測は全て取り下げます.
無責任な発言をして,申し訳ありませんでした. ■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■
>電位差計は高校物理でも扱われる素材だと思います.
返えす言葉が見当たりません.素人の感じですが,高校の物理教育に於いては,もっと大切な事をじっくり教えるべきだと思います.
さらに,「電位差計」の場合:逆起電力を掛けるときには,ボンと逆起電力を掛けてはいないと思いますし,当然のこととして,その操作を熟知して操作するとおもいます.そのような留意事項があって使われることまで,高校教育で出来ているのでしょうか?とても疑問です.それとも物理実験などで体験学習でもあるのでしょうか?
以前,MXKさんは,「学生の指導云々」といった記述をされていたと思います.そのような発言を見ている学生さん達には,強い影響力をお持ちになっている点を,十二分にご理解いただきたい,と思います.老人の杞憂であれば,お許し下さい.
Re: 2004東工大前期の問題です
MXK さんのレス (2007/02/23(Fri) 13:25)
zoroさん,
あまり物理以外の発言はしたくないのですが,せっかくいただいた ご意見等をうけとめる意味からも,失礼を承知で敢えて返答させていだたきます.
まず,普段より高校生,学部生からの質問に対して,時間と手間を惜しまずに丁寧に 答えておられる姿勢には敬意を表したいと思います.
> 関連して申し上げると,私は現在の高校教育での物理を全く存じません.
そういう認識をお持ちでしたら,図書館や書店に出かけられた折にでも, 高校の参考書などをご覧になるのがよいように思います.
> 恐らく,ご自分の研究室に所属されている学生さん達をご指導されている...
一般論として,投稿者の背景を云々することは不適切だと思います.とくに本人が明示的に のべていない,不確かな根拠に基づいている場合はなおさらです.この掲示板はバックグラウンド の違いを超えた対等な立場での交流の場であることに意義があると理解しています.
わたしの短文が分かりにくい場合は,分からない方から直接に「ここが,このように分かりにくい」と 具体的にいっていただければ十分かと思います.
>「起電力・逆起電力の混成系」の問題が,...
正確には「電源において起電力に反する向きに電流が流れる場合」が,というべきです. 「逆起電力」は他の意味を持っています.
> 素人の感じですが,高校の物理教育に於いては,もっと大切な事をじっくり教えるべきだと思います.
このように,問題等を評論されることは結構ですが,「私は現在の高校教育での物理を全く存じません.」 という状況でのご発言であることにある種の矛盾,違和感を感じています. いまの場合でも,「電位差計」がどのような形で教育素材として利用されているかを参考書等で調べる前に, 上記のように断定されることが私には理解できません.
また,少し前の記事にあった,
> さて,コンデンサの一部が動くと言う,アクロバティックな問題を観察してきたので,
も何か難問奇問のような印象を与えかねないご発言ですが,私は比較的標準的な問題だと 思っています.質問者が当初示された予備校のページにも「難易度=標準」と書かれていました. 前にもどこかで書きましたが,文脈や状況を理解しないで,主観的に問題批評をすることは, 控えたいと思っています.
> 強い影響力をお持ちになっている点を,十二分にご理解いただきたい,と思います.
これはこの掲示板のメイン回答者の1人であるzoroさんに一層あてはまると思いますので, よろしくお願いします.
Re: 2004東工大前期の問題です
zoro さんのレス (2007/02/23(Fri) 15:29)
>> 関連して申し上げると,私は現在の高校教育での物理を全く存じません. > >そういう認識をお持ちでしたら,図書館や書店に出かけられた折にでも, >高校の参考書などをご覧になるのがよいように思います.
すぐ近くの図書館には,高校の教科書は存在しませんでした.高校の参考書がどこまで正しい教育内容を把握しているかは疑問です.三省堂にでも行く機会がありましたら教科書を入手はしたいですが,この論議には間に合いません.
>> 恐らく,ご自分の研究室に所属されている学生さん達をご指導されている... > >一般論として,投稿者の背景を云々することは不適切だと思います.とくに本人が明示的にのべていない,不確かな根拠に基づいている場合はなおさらです.この掲示板はバックグラウンドの違いを超えた対等な立場での交流の場であることに意義があると理解しています.
これについては,推測が混入していると思います.しかし,toorisugari no Hiroさんとのやり取りを拝見していると,あきらかに指導者としての発言「(よ)」をされていますし,MXKさんから出された課題を巧く達成できないとため息さえ書かれています.その他のご発言からも,そのように感じています.どうしてもご不満なら,それらの部分を削除された方がいいかも知れませんね.
私は,物理の論議であるかぎり,中学生さんであろうと,物理学会の会長さんであろうと,ノーベル賞をうけられた碩学さんであっても,対等の立場で自由闊達な論議がしたいとおもいます.そのとき,変な権威や難しい語彙,不必要に難解な数式を使ってははフェアな論議にならないと思うだけです.
例えば,このスレッドは,普通だったら数行の式で終わる回答を,丁寧に式を立てて,回答を吟味しただけのものです.その論議のなかから出て来た「副次的疑問をどう考えるか」に答えようとしただけですよ.なにも高校の教育内容を厳密に知らなければ答えてはならないとも思いません.
>わたしの短文が分かりにくい場合は,分からない方から直接に「ここが,このように分かりにくい」と具体的にいっていただければ十分かと思います.
それは場合に依ります.あまりにも短すぎて,どこから質問して良いやら判らない,という場面が大半なのだと思います.
>>「起電力・逆起電力の混成系」の問題が,...
>正確には「電源において起電力に反する向きに電流が流れる場合」が,というべきです.「逆起電力」は他の意味を持っています.
なるほど,「起電力・それに逆方向の起電力との混成系」の問題が,...と書くべきでした.
「逆起電力」とはリアクタンス成分と限定的に使えば宜しいのでしょうか?
>> 素人の感じですが,高校の物理教育に於いては,もっと大切な事をじっくり教えるべきだと思います.
>このように,問題等を評論されることは結構ですが,「私は現在の高校教育での物理を全く存じません.」という状況でのご発言であることにある種の矛盾,違和感を感じています.
>いまの場合でも,「電位差計」がどのような形で教育素材として利用されているかを参考書等で調べる前に,上記のように断定されることが私には理解できません.
静電気現象に良く出て来る「接地」の解釈,電源の意味(電位差を保持する事,信号としての電荷について低インピーダンである事)が明確にされないまま,不完全に教育が進行してしまうのが本当の問題点だろうと思います.むしろ電位差計などを教えるより,接地・電源・電池の考え方をクリア・カットに教えるべきだろうと思うだけです.
特に,理学部の物理教育の視点で見ていると,高校生の段階で,なんでそこまで細かい知識が要求されるのかが不思議です.そのくせ,数学が遅すぎたり....
>また,少し前の記事にあった,
>> さて,コンデンサの一部が動くと言う,アクロバティックな問題を観察してきたので,
>も何か難問奇問のような印象を与えかねないご発言ですが,私は比較的標準的な問題だと思っています.質問者が当初示された予備校のページにも「難易度=標準」と書かれていました.
私は,予備校のページが見難いのでpdfしか見ていませんでした.まして,「難易度=標準」というのを仮に見たとしても,何のことか理解できません.
むしろ,このスレッドを始めからお読みになれば,私が戸惑いながらこの問題に接し,図示し,解き,感じた所を書いたのが判るはずです.その纏めとして自分の感想として書いたものであります.そこでは,この問題の出題者さんの創意工夫には敬意を表しています.私の書いた一部について,コンテキストを考慮せずに論評されるのは,当方に対する言われなきご批判とおもわれます.
>前にもどこかで書きましたが,文脈や状況を理解しないで,主観的に問題批評をすることは,控えたいと思っています.
う〜む.
>> 強い影響力をお持ちになっている点を,十二分にご理解いただきたい,と思います. > >これはこの掲示板のメイン回答者の1人であるzoroさんに一層あてはまると思いますので,よろしくお願いします.
私は,自分で理解できたと思う点を,丁寧に書いている積もりです.MXKさんのように一を聴いて,百・千の理解を求めようとしません.
#仲間内の論議でしたら,かなりシビアな論議をすることは在りますし,ショート・カットな論議がすきです. #とくに心身ともに復調するとともに,昔の毒舌がもどってきたと言われますから.
しかし,この掲示板では,なるべく十を書いて,一を表せたらいいな,と思っています.ご覧になった方の目から見て,不必要な部分は端折ればいいと思うからです.それが色々なバックグランドを持つ人々が気楽に物理をエンジョイし,自分の目で問題に挑戦する機会に繋がると思うからです.
他方,高度な物理数学とか応用数学などの論議を延々とするのも良いでしょうね.しかし,その問題の前提がなにか判らないまんま,進んでも掲示板の愛好者には理解されないように思います.
私のばあい,物理はシンプルであるが強力な理解ツールだとおもいます.このスレッドもそのようなポリシで進められた事を嬉しく思います.
Re: 2004東工大前期の問題です
toorisugari no Hiro さんのレス (2007/02/23(Fri) 15:43)
MXKさん側の発言だととってほしくないです.
> これについては,推測が混入していると思います.しかし,
中略 > どうしてもご不満なら,それらの部分を削除された方がいいかも知れませんね.
こういう発言はやめてくださいませんか. zoroさんは「老人」だとどこかで書いておられました.zoroさんが大人か実は中学生か,関心はないですが,とりあえず,大人と言明されているのですから,こういう「くだらない」論争方式はやめてください.
大人の発言ではありません.
> そのとき,変な権威や難しい語彙,不必要に難解な数式を使ってははフェアな論議にならないと思うだけです.
初心者向けに書かねばいけないと言う隠れ蓑で, 自分が理解出来ないものを排除する論法はやめてください.
大人の発言ではありません.
Re: 2004東工大前期の問題です
MXK さんのレス (2007/02/23(Fri) 17:31)
toorisugari no Hiroさん,
toorisugari no Hiro さんが引き合いに出されるのは想定外でした. 申し訳ありませんでした.
Re: 2004東工大前期の問題です
zoro さんのレス (2007/02/23(Fri) 17:41)
>toorisugari no Hiroさん,
このスレッドは少なくとも平行版コンデンサに関係する論議をしています.全く関係のない論議をするのならば,別途スレッドを立てて論議下さい.
なお,私は老人であることを,No.14546 で明言しています.中学生でも,大学生でも,大学院生でもありません.健康を害したものの,この数式掲示板の御蔭で,頭も回復した為に,物理の幅広い理解のお手伝いをしたくて書き込みをしているだけです.
あなたこそ,大人・中学生などと,わざと誤解を生じさせる書き込みをしないでください.まえにも大学1年か大学院1年かといった詮索をされていましたね.
願わくば,No.14558を削除して,別スレッドで,こころおきなくご発言をお願いします.そうして戴ければ,この発言,No.14563も削除致します.
受験生さんのスレッドは尊重してください,お願いですから.老人より.
Re: 2004東工大前期の問題です
toorisugari no Hiro さんのレス (2007/02/23(Fri) 17:46)
zoroさん 私の発言を撤回するつもりはありません.先の発言はあなたの言動の鏡とおもってください.
MXKさん,気になさらないでください. 実生活はともかく,ここでは,私はMXKさんの生徒ですから.:-)
先の発言は,中立な立場でいってます. また,卑怯なレトリックや幼稚な反論方法に異議を唱えているだけです.(このような直接的な言葉を使いたくなかったので,あのような言い回しを使いました.) 内容に触れませんし,人格攻撃するつもりはありません. 念のため >zoro さん
あと,蛇足ですが,私が強い口調になるのは,「りんご」さん「zoro」さんはともかく, mNejiさんが好きで,今後も,この掲示板にいてもらいたいからです. (そうでなかったら黙殺しています.)
(そういう意味では中立ではないな...)
Re: 2004東工大前期の問題です
toorisugari no Hiro さんのレス (2007/02/24(Sat) 14:36)
zoroさん
提案ですが,14546中の不適切な発言を削除していただき,続く,スレッド も本筋と関係ない部分を削除(あるいは記事ごと削除)していただければ,14558 は削除します.(たぶんMXKさんも本筋と関係ない議論を削除することに同意されると思います.)
受験生のためとおっしゃりますが,間違いを指摘されたときに,適切な対応をとらず, 余計なことを言い出したのはzoroさんであり,本筋を離れたのはzoroさんの責任です.
それを正しいものに換えていただければ,私の書き込みはすべて消します.
Re: 2004東工大前期の問題です
zoro さんのレス (2007/02/24(Sat) 15:05)
toorisugari no Hiroさん,
ご指摘の発言のなかで,第三者であるtoorisugari no Hiroさんに関係する部分はないとおもいます.いくらお師匠さんと私の論議の中で,問題があると思っても,横から急にいわれても困ります.
何度も言いますが,静電気の論議をしているスレッドに無関係のチャチャをしないで下さい.せめて,別にスレッドを立てたら如何ですか.
Re: 2004東工大前期の問題です
toorisugari no Hiro さんのレス (2007/02/25(Sun) 07:27)
そのようにお考えでしたら,私の発言は削除できません.
くどいですが,MXKさん側としての発言ではないです. お得意の曲解をされて残念です.
# そもそも,掲示板以外では,MXKさんとは何の関係も面識もないです.って言う必要もない当たり前のことですね.また,よく議論するからMXKさんの味方してると思われたら心外です.そこまで偏狭ではないです.