素数
素数
ハーツ さんの書込 (2007/02/02(Fri) 19:45)
はじめまして.学年は高2です.
数学の問題なのですが(しかも高校数学),他の掲示板等ではちゃんとした解答が得られなかったので,答えていただけないでしょうか?以下の問題です.
p,2p + 1,4p - 1,6p - 1,8p + 1 がいずれも素数であるような p をすべて求めよ.
予想ではp=2,5ぐらいしかないと思うのですが,どうでしょうか?よろしくお願いします.
Re: 素数
りんご さんのレス (2007/02/03(Sat) 00:16)
ハーツさん,初めまして.
純粋に数学の問題ですけど,私は,泥臭い方法でアプローチしたいと思います.
とりあえず,エクセル表計算で,p=2...34 を書き出してみました.暗算が不得意なので,数値が100を超えると,もう駄目ですね.とりあえず,簡単なルール
・偶数は駄目, ・1桁めが0,5は駄目 ・1桁めが3で,かつ全桁の総和が3の倍数ではだめ.
なんてやってみたものの,p=15で出てくる,121で挫折しました.
やはり,ごり押しでも,判定するには素数計算の簡易サブルーチンが欲しいな,という単純な結論にいたりました(笑).
==== 書いたのを見て11^2を思い出しました.;P)
Re: 素数
Joh さんのレス (2007/02/03(Sat) 00:48)
5で割った余りを考えてみます.
(場合1)p=5の場合: 題意を満たす.
(場合2) pを5以外の素数と仮定すると,5で割ったときの余りは,1,2,3,4のいずれかになるはずです.
ところが,余りが1の場合6p-1の,余り2の場合2p+1の,余り3の場合8p+1の,余り4の場合は4p-1の余りがそれぞれ0になってしまいます.これが,10以上の5の倍数になるようでは素数であるという仮定に反するので,考えられるのは次の場合だけになります.
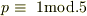 で,
で, 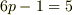 の場合.
の場合.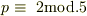 で,
で, 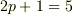 の場合.
の場合.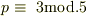 で,
で, 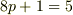 の場合.
の場合.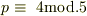 で,
で, 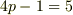 の場合.
の場合.
pが素数となるようなのは,(ii)のp=2だけですから,(場合1)とあわせて,答えは2と5です.■
Re: 素数
Joh さんのレス (2007/02/03(Sat) 00:51)
蛇足ですが,素数は無限にあるので,りんごさんのようなやり方では,どんなに素晴らしいサブルーチンがあろうと,全く証明にはなりません.
Re: 素数
ハーツ さんのレス (2007/02/03(Sat) 19:08)
りんごさん,Jhoさん,お返事ありがとうございます.
整数・素数問題は論理が厄介なのが多いですが,これからもがんばりたいと思います.
Re: 素数
りんご さんのレス (2007/02/03(Sat) 20:55)
結局,簡単な素数判定サブルーチンを作って見ました(笑).p=113まで計算したものの,その範囲では同時に素数になる組は在りませんでした.p=53でちょっとあわてましたよ,右端が画面から出ていたのですが.
素数について大学の入試問題点に出題されると知って,驚いています.楽しみながらベストを尽くされますように.