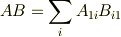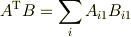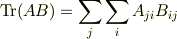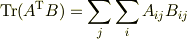行列
行列
高橋聡 さんの書込 (2007/02/02(Fri) 18:28)
はじめまして. 二点ほど行列に関して質問させていただきたいことがあります. ?Aは正方行列じゃない(eg:n×1)とすると,A^2=AA^Tと考えるべきなのでしょうか.もしくはそのように考えるときもあるのでしょうか. ここで,Tは行列の転置を示しています. ?行列のノルムがトレースで定義されることを示すのが私にとっては大変難しい問題です. どうか,上記の二点についてアドバイスをいただけないでしょうか. よろしくお願いします.
Re: 行列
高橋聡 さんのレス (2007/02/05(Mon) 00:33)
MXKさん
ご返信有難うございました. 3番目の形は計算できないように思います. 4番目はよく意味が理解できませんでした. Trは対角成分の合計を示していると思うのですが, ヒントを頂いて大変恐縮なのですが,私にとってはこれらの情報で現在の問題を解決することが出来ません. もしよろしければ,もう少し進んだヒントがいただければ幸いです. どうか宜しくお願いします.
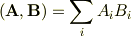
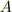 は1行
は1行  列,
列, 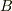 は
は