図形の複雑さについて

やなぎさんの書込 (2007/01/31(Wed) 23:14)

はじめまして，やなぎと申します．テストの問題について調べていたところ，偶然このサイトを見つけました．早速質問ですが，『多角形にはさまざまな形があるが，それらの違いを評価するにはどうしたらいいか』という問いについてです．自分で調べてみたところ，『図形の複雑さ』というものがあるのはわかったのですが，その評価法までは調べられませんでした．この問題について，何か教えて頂ければありがたいです．くだらない質問で大変申し訳ないのですが，どうぞよろしくお願い致します．

Re: 図形の複雑さについて

Joh さんのレス (2007/02/01(Thu) 00:38)

はじめまして．とても面白そうな問題ですが，図形の違いを評価する，という意味が私にはよく分かりませんでした．多角形というのは，正多角形のことでしょうか？図形の複雑さ，というのも浅学にして分かりません．

できれば一緒に考えてみたいので，もう少し詳しく（問題の背景や，今までに勉強したこと等）教えてください．

Re: 図形の複雑さについて

CO さんのレス (2007/02/01(Thu) 00:42)

どういう風に評価したいのでしょうね．正 n 角形からのズレを調べるとかでしょうか．

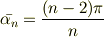
$\bar{\alpha_n} = \frac{(n-2)\pi}{n}$

と定義して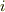番目の頂点の角を 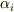$\alpha_i$ などとし，

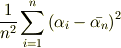
$\frac{1}{n^2}\sum_{i=1}^{n} \left( \alpha_i - \bar{\alpha_n}\right)^2$

みたいな量で評価できないでしょうか． (# まったく思いつきで適当言ってますので，的はずれだったら無視してください)

Re: 図形の複雑さについて

なんとなくさんのレス (2007/02/01(Thu) 09:38)

こんにちは．私もまったくの思いつき＆素人考えですが，「図形の複雑さ」というと，ありきたりですが，「フラクタル次元」数で評価する，と浮かびます．ものすごく簡略化して言えば（しか言えない，笑），その図形の周長÷面積などですが，いろいろ考えられますね．複雑な領域を構成するには辺の形状を複雑にし，どんどこ1次元から2次元平面へ埋め込んでいく・・・というイメージでしょうか．まあ，でもこれもある考え方の一つに過ぎませんね．

Re: 図形の複雑さについて

りんごさんのレス (2007/02/01(Thu) 10:36)

やなぎさん，初めまして．

「1/f揺らぎ」を研究されている武者先生の所で拝見したのですが，「景観の評価」に「1/f揺らぎ」を使うお話をされていました．どこかの自治体での町並みデザインをしながら，その定量的な評価をするのだよ，とお話されてのを思い出しました．

上の例は3Dですが，２次元情報の評価につながるかなと思います．あくまで素人の憶測ですが...．

Re: 図形の複雑さについて

やなぎさんのレス (2007/02/01(Thu) 19:06)

皆さんとてもご親切にありがとうございます！！答えは式で出すように，という事なので，とても助かりました．

質問についてですが，大変不十分で申し訳ありません．図形の違いというのは，例えば十角形なら，正十角形や星型などの違いについてです．

フラクタル次元については調べてみたのですが，どうも自分には理解力が足りなかったようで… この事例に適応しても大丈夫でしょうか？

Re: 図形の複雑さについて

なんとなくさんのレス (2007/02/01(Thu) 23:35)

フラクタル次元は正確には「ハウスドルフ次元」で，多角形，つまり通常の曲線ではどれでも「１」ですから，比較には適用できないでしょうね．周長÷面積ももっとも小さくなるのは平面では円，立体では球ですから円（球）が最もシンプルな図形ということになりますが，実際どうなんでしょう．円ならその属性は”半径”という一つの物差しのみで決まるので，やっぱり最もシンプルかも．フラクタルで良く出るペアノ曲線やコッホ曲線は複雑そうに見えますが，その構成手順（言うなればプログラムステップ）は数ステップです．このステップ数を評価にする（作画手数でもいいかも）こともできそうです．「複雑さ」の定義付けは難しいですね．では，逆に「シンプル」な図形とは何かと考えれば，対称性の高い図形である，というのも一つの答えでしょう．なぜなら，回転，鏡映などで，自分自身に戻るということは，部分相違性の欠如に他ならないからですね．したがって，たとえば１０角形なら10角形と言う制限のなかで複雑性を定義できるような特徴を抽出する必要がありますね．ＣＯさんの提案されたことをヒントにオリジナルを考えてみられてはどうでしょう．たとえば，多角形なら，所詮は線分と角度の集まりですから，その種類を勘定する手もありますね．私の勘（笑）では，「正解」というものは無いんじゃないでしょうか．長い割に，大してお役に立てる内容でないと気付きました．まあ，参考までに．

Re: 図形の複雑さについて

やなぎさんのレス (2007/02/01(Thu) 23:57)

なんとなくさん返信ありがとうございます．

これを元に自分でも考えてみます．本当に参考になりました，ありがとうございます！！

Re: 図形の複雑さについて

りんごさんのレス (2007/02/02(Fri) 00:47)

一般的な説明は出来ませんが，ある一定な半径に内接する多角形を考えます．

その内で，説明のしやすそうな円（直径D）と正四角形（辺Dで比較するとします．

いまデカルト座標xyの原点に２つの図形の重心があり，正四角形の辺は座標軸に平行とします．

このとき，図形の形状にそった位置についてxy座標の２次元フーリエ展開を行い，空間波数kをだせば，

（１）円では，kはDから短波長まで連続的に分布し（２）正四角形では，k＝Dしか無い

という風にスペクトル的に差が出るような気もします．おそらく「スペクトルの複雑性」〜「図形の複雑性」みたいな関係がありそうだと感じます．

＝＝＝＝と書いたものの，

極座標にすると全然違いそうな気もします．でもそれはそれで，別の判定を出せるかも．角度の周期性みたいな話だろうから，COさんの説と同じになるのかも知れませんね．

[home] [掲示板] [ページの先頭]